[PYTHON] Vector representation of simple words: word2vec, GloVe
I've been watching the video and slides of a class called "Deep Learning for Natural Language Processing" at Stanford University recently, but I just watched it. I decided to publish the lecture memo while summarizing the contents because it seems that it will not remain in my body.
This time is the second "Simple Word Vector representations: word2vec, GloVe". The first time was an intro so I skipped it.
How to express the meaning of each word and its problems
If you want your computer to recognize the meaning of a word, you can use a hand-made classification table such as WordNet. However, there is a problem with such expressions.
-It does not express fine nuances (differences in synonyms such as adept, expert, good, practiced, proficient, skillful) --I can't handle new words --Subjective --Human must do his best --Difficult to calculate accurate word similarity
That's why trying to express the meaning of each word doesn't work very well.
Focus on distribution similarity: word co-occurrence matrix
The similarity of words can be considered by the distribution of words appearing around in the document set, not by the linguistic meaning of the words. This is one of the most successful ideas in modern statistical NLP.
For example, if you have two sentences where the word "banking" appears

I think that the word painted in orange stands for "banking".
To make this model workable on a computer, the co-occurrence relationships between words can be represented by a matrix. There is an option to make the size of the orange part the whole document or up to N characters before and after (this range is called a window), and by providing a window, the word can be in the document It can be said that the position and meaning of appearance can be taken into consideration. Windows are generally 5 to 10 in size. You can change the weight on the left and right of the word, and you can also weight the word according to its distance.
Example of word co-occurrence matrix
- I like deep learning.
- I like NLP.
- I enjoy flying.
The co-occurrence matrix when the document is a corpus, the window size is 1, and the weights are the same on the left and right of the word:

Problems with word co-occurrence matrix
――Since the number of dimensions increases according to the words that appear, the larger the corpus, the larger and sparse matrix becomes. ――If the number of dimensions increases, a large amount of storage capacity may be required unless devised.
In short, it lacks robustness.
The basic idea for these problems is to make them smaller and denser by extracting only the important information, rather than queuing everything. Generally, I want to compress it to about 25 to 1000 dimensions. So how do you do that?
Make the word co-occurrence matrix dense
Several methods have been proposed. Here, we will take up SVD, word2vec, and GloVe.
SVD
The first method is to perform singular value decomposition (SVD) of the matrix. SVD is implemented in numpy so you can try it out.
import numpy as np
la = np.linalg
words = ["I", "like", "enjoy", "deep",
"learning", "NLP", "flying", "."]
#↑ Word co-occurrence matrix that I worked hard to enter manually
X = np.array([
[0,2,1,0,0,0,0,0],
[2,0,0,1,0,1,0,0],
[1,0,0,0,0,0,1,0],
[0,1,0,0,1,0,0,0],
[0,0,0,1,0,0,0,1],
[0,1,0,0,0,0,0,1],
[0,0,1,0,0,0,0,1],
[0,0,0,0,1,1,1,0]
])
# SVD
U, s, Vh = la.svd(X, full_matrices=False)
This makes the originally sparse word co-occurrence vector dense. For example, for the word "deep"
>>> print(X[3])
[0 1 0 0 1 0 0 0]
It was
>>> print(U[3])
[ -2.56274005e-01 2.74017533e-01 1.59810848e-01 -2.77555756e-16
-5.78984617e-01 6.36550929e-01 8.88178420e-16 -3.05414877e-01]
become. It's kind of like this, but when I take only the 0th and 1st dimensions and plot each word in a 2D space, somehow "deep" and "NLP" are close to each other, or "enjoy". It seems that "and" learning "are similar to each other.
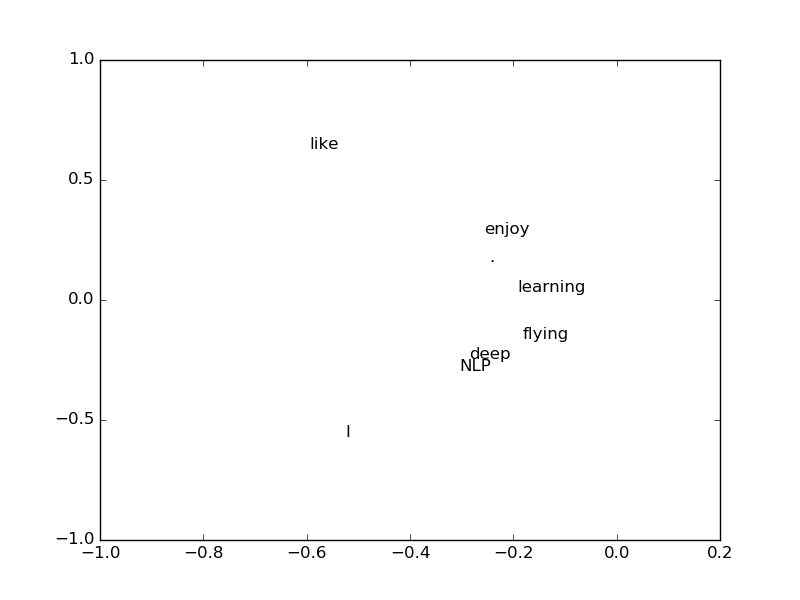
Contents of SVD
By the way, I feel that the validity of using SVD was not mentioned in the lecture. Since I mentioned "Latent Semantic Analysis", it may be that you should look there.
Using SVD, the $ n \ times n $ matrix $ X $ of rank $ r $ is the column orthogonal matrix $ U $ and $ V $ of $ n \ times r $, and the diagonal element of $ D $. Using the $ r \ times r $ matrix $ S $ with singular values arranged, it can be decomposed as follows.
X = U S V^T
At this time, if you put $ S V ^ T $ as $ W $
X = U W
become. It can be said that $ X $ is some kind of matrix $ W $ converted by $ U $. By the way, since $ U $ is a column orthogonal matrix, the column vectors are independent of each other. In other words, it is the basis of some space, but it is actually a word space, and each column vector can be thought of as representing a potential meaning.
Problems with SVD
SVD can also be generalized and applied to the $ n \ times m $ matrix. If $ n <m $, the calculation cost to calculate from such a matrix is $ O (mn ^ 2) $, so the huge size cannot be applied to the matrix. That's why it's difficult to incorporate new words when they come out.
word2vec
Various methods have been proposed, but word2vec proposed by Google's Mikolov et al. In 2013 is drawing attention.
The idea of word2vec is "not to deal directly with the number of co-occurrence, but to deal with the words that appear in the surroundings stochastically". It's faster and easier to add new words.
word2vec is also C language, Java, [Python](http://radimrehurek. There is an implementation in com / gensim /) so you can try it.
theory
Consider a window of size c before and after each word, consider the probability that it will appear there for each word in the window, and use the sum of them as the objective function to perform maximum likelihood estimation. The logarithm is taken to make it easier to calculate later.
J(\theta) = \frac{1}{T} \sum_{t=1}^T \sum_{-c \leq j \leq c,j \neq 0} \log p(w_{t+j} | w_t)
Vector relationship
Words are represented as vectors using word2vec. At this time, it is known that an interesting result can be obtained from the difference between word vectors.
For example, subtracting Man from King and adding Woman makes it very close to Queen's vector. It can be thought that the vector created by subtracting Man from King represents some powerful concept.
X_{king} - X_{man} + X_{woman} \approx X_{queen}
There seems to be a story that if you analyze the Japanese corpus with mecab and do the same thing, you pull Yahoo from Google and add Toyota, and it becomes Nissan.
- https://plus.google.com/107334123935896432800/posts/JvXrjzmLVW4
speed
word2vec can learn at high speed even for a huge corpus. It seems that he was able to learn a corpus of about 2GB, which is a bz2 compressed Japanese Wikipedia document, in about 30 minutes.
-Until I run word2vec without knowing anything about natural language processing: Most likely diary
I used to try LDA on Japanese Wikipedia using GenSim, but I remember it took half a day at that time. Even if it is implemented in C language and the machine specs are higher than at that time, there is no doubt that word2vec is overwhelmingly faster.
GloVe
We have seen that there are SVD-like methods based on the number of occurrences of words and word2vec-like probabilistic approaches, but each has its advantages and disadvantages.
--Method based on the number of appearances ――A small corpus can learn at high speed, but a large corpus takes time. ――It is used to measure the similarity of words, but words that appear less frequently can gain disproportionate importance. --Probability-based method --You have to have a big corpus. --Complex patterns other than word similarity can also be measured.
A method called GloVe, which combines the two worlds and cousins, is ([Richard Socher](http: // www) who is in charge of this lecture. Proposed by a group of .socher.org/) et al.
--Fast learning -Can handle large corpora --Small corpus, good performance even with small vectors