[PYTHON] [Statistik] Erste "Standardabweichung" (um Frustrationen mit Statistiken zu vermeiden)
Für diejenigen, die Statistik lernen wollen, gibt es meiner Meinung nach eine "Standardabweichung", die ein sehr wichtiges Konzept ist, aber schwer zu verstehen ist. Ich kenne es bis zum "Durchschnitt" und ich denke, es fühlt sich an wie "Ich verstehe", aber die "Standardabweichung", die plötzlich auftritt.
\sigma = \sqrt{ {1 \over n} \sum_{i=1}^n(x_i - \bar{x})^2}
Mauer von. Ich denke, es gibt einige Leute, die von der Tatsache überwältigt wurden, dass "Mathe unmöglich ist" hier.
Wenn Sie zuerst das Bild des Diagramms veröffentlichen, ist die Länge der roten Linie unten die "Standardabweichung". Wir werden auch klären, warum diese Länge die Standardabweichung ist.
 (code is here)
(code is here)
In diesem Artikel werde ich erklären, wie hoch die Standardabweichung von 1 ist, damit auch diejenigen, die nicht gut in Mathematik sind, sie verstehen können. Ich werde es erklären, damit selbst diejenigen, die die Formel verstehen, aber die Bedeutung von "Standardabweichung" nicht verstehen, sie intuitiv verstehen können. Schauen Sie also bitte mal rein.
(* In diesem Artikel wird $ n $ als Nenner der Standardabweichung verwendet. Es gibt Fälle, in denen $ n-1 $ verwendet wird, und es wird je nach zu analysierendem Fall ordnungsgemäß verwendet, hier jedoch der mit der einfachsten Notation $ Ich werde es mit n $ erklären.)
</ i> 0. Über Symbole
Wenn Sie mit Mathematik nicht vertraut sind, ist das erste, was Sie stolpert, das Symbol der Mathematik. Was ist "$ x_i $"?
\sum_{i=1}^n x_i
Dies ist eine Erklärung für diejenigen, die erfrischend sind. Wenn Sie mit den mathematischen Symbolen hier einverstanden sind, springen Sie bitte zu [Nächster Abschnitt](http://qiita.com/kenmatsu4/items/e6c6acb289c02609e619#1 Wie auch immer, Durchschnitt).
Beginnen wir zunächst mit $ x_i $.
Jeder benutzt Excel, oder? Angenommen, Sie haben Daten für einen solchen Test.
| Name | Mathematik |
|---|---|
| Tanaka:smile: | 96 |
| Takahashi:flushed: | 63 |
| Suzuki:stuck_out_tongue: | 85 |
| Watanabe:stuck_out_tongue_winking_eye: | 66 |
| Shimizu:laughing: | 91 |
| Kimura:grin: | 89 |
| Yamamoto:smirk: | 77 |
Insgesamt
Gesamtpunktzahl=Tanaka(Mathematik) +Takahashi(Mathematik) +Suzuki(Mathematik) +Watanabe(Mathematik) +Shimizu(Mathematik) +Kimura(Mathematik) +Yamamoto(Mathematik)
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
Kann berechnet werden als.
Wenn die ID anstelle des Namens verwendet wird
| ID | Mathematik |
|---|---|
| 1 | 96 |
| 2 | 63 |
| 3 | 85 |
| 4 | 66 |
| 5 | 91 |
| 6 | 89 |
| 7 | 77 |
Gesamtpunktzahl= {\rm ID}:1(Mathematik) + {\rm ID}:2(Mathematik) + {\rm ID}:3(Mathematik) + {\rm ID}:4(Mathematik) + {\rm ID}:5(Mathematik) + {\rm ID}:6(Mathematik) + {\rm ID}:7(Mathematik)
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
ist. Versuchen Sie, die Partitur durch eine Variable anstelle einer Zahl zu ersetzen. Die Punktzahl für eine Person mit ID: 1 beträgt $ x_1 $. Die Nummer unten rechts steht für die ID. Dann lautet die Formel für die Gesamtpunktzahl
Gesamtpunktzahl= {\rm ID}:1(Mathematik) + {\rm ID}:2(Mathematik) + {\rm ID}:3(Mathematik) + {\rm ID}:4(Mathematik) + {\rm ID}:5(Mathematik) + {\rm ID}:6(Mathematik) + {\rm ID}:7(Mathematik)
\\
= x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
Wird ausgedrückt als. Bis zu diesem Zeitpunkt gab es 7 Daten, daher hätte ich die Ergänzungen wie oben beschrieben stetig anordnen sollen, aber wenn es 1000 Daten gibt, ist es nicht sehr gut, aber ich kann es nicht schreiben.
Hier bietet sich $ \ sum $ an!
Gesamtpunktzahl= {\rm ID}:1(Mathematik) + {\rm ID}:2(Mathematik) + {\rm ID}:3(Mathematik) + {\rm ID}:4(Mathematik) + {\rm ID}:5(Mathematik) + {\rm ID}:6(Mathematik) + {\rm ID}:7(Mathematik)
\\
= x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7
\\
= \sum_{i=1}^7 x_i
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
Es wird ausgedrückt als. Mit anderen Worten

Damit
\sum_{i=1}^7 x_i = x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7
Wird sein. Auf diese Weise auch bei 1000 Daten
\sum_{i=1}^{1000} x_i = x_1 + x_2 + \cdots + x_{1000}
Es wird verwendet, weil es praktisch ist, weil es ausgedrückt werden kann als.
Erstens ist es nicht unmöglich, 1000 Teile hintereinander zu schreiben, wenn die Anzahl im Voraus festgelegt wird, aber die Anzahl der Daten ist derzeit nicht bekannt, und selbst wenn sie vorerst vorübergehend als $ n $ Teile platziert werden ,
\sum_{i=1}^{n} x_i
Sie können schreiben, auch wenn Sie sich nicht entschieden haben! Praktisch!
Übrigens, wenn Sie wissen, wie man es in Code ausdrückt, können Sie es möglicherweise sofort verstehen, indem Sie sagen, dass es der folgende Prozess ist. Das Symbol $ \ sum $ ist ein Vorgang zum Drehen und Hinzufügen mit einer for-Anweisung.
sum.py
x = [96, 63, 85, 66, 91, 89, 77]
total = 0
for i in range(len(x)):
total += x[i]
print total
</ i> 1. Wie auch immer, zunächst einmal durchschnittlich
Lassen Sie uns noch einmal über "Durchschnitt" nachdenken. Es gibt verschiedene Arten von Durchschnittswerten, wie "arithmetischer Durchschnitt", "geometrischer Durchschnitt" und "harmonischer Durchschnitt", aber der sogenannte bekannte "Durchschnitt" ist "arithmetischer Durchschnitt".
Es sind alle Daten, die addiert und durch diese Zahl geteilt werden. In der Statistik wird dieser "Mittelwert" als $ \ bar {x} $ ausgedrückt, und die Definition lautet wie folgt. Die Anzahl der Daten beträgt $ n $. Im Beispiel des Mathe-Tests im vorherigen Abschnitt ist es $ n = 7 $, da es sich um die Daten von 7 Schülern handelt.
\bar{x} = {1 \over n} \sum_{i=1}^{n} x_i
(Wenn Sie die Bedeutung des Symbols nicht verstehen, lesen Sie bitte den [vorherigen Abschnitt](http://qiita.com/kenmatsu4/items/e6c6acb289c02609e619#0 Symbol))
Die Grafik ist wie folgt. Das ist intuitiv: erröten:
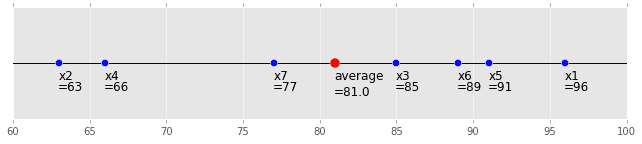 (code is here)
(code is here)
</ i> 2. Was ist "Abweichung"?
Als nächstes werde ich das Konzept der "Abweichung" erklären. Wie Sie sehen können, ist "Standard ** Abweichung **" etwas näher am Kern.
Die Abweichung ist die Differenz zwischen den einzelnen Daten und dem Durchschnitt, wie unten gezeigt.
| ID | Ergebnis | Abweichung |
|---|---|---|
| 1 | 96 | 96-81= 15 |
| 2 | 63 | 63-81= -18 |
| 3 | 85 | 85-81= 4 |
| 4 | 66 | 66-81= -15 |
| 5 | 91 | 91-81= 10 |
| 6 | 89 | 89-81= 8 |
| 7 | 77 | 77-81= -4 |
Dies wird auch durch ein Diagramm dargestellt. Die rote Linie ist die Abweichung der einzelnen Daten.
<! - Der Standardwert dieser Abweichung ist die "Standardabweichung". ->
 (code is here)
(code is here)
</ i> 3. Durchschnittliche Abweichung
Bevor ich zur Standardabweichung übergehe, möchte ich eine "durchschnittliche Abweichung" einführen, die intuitiv leicht zu verstehen ist.
Dies ist der Durchschnitt der im vorherigen Abschnitt erläuterten "Abweichungen". Mit anderen Worten
| ID | Abweichung |
|---|---|
| 1 | 15 |
| 2 | -18 |
| 3 | 4 |
| 4 | -15 |
| 5 | 10 |
| 6 | 8 |
| 7 | -4 |
Ich denke an den Durchschnitt von, aber es gibt nur ein Problem, und wenn Sie alle hinzufügen, wird es 0 sein.
Was ich machen will; was ich vorhabe zu tun
 Da es sich um die durchschnittliche Länge der roten Linie von handelt, wird das Minus weggelassen.
Da es sich um die durchschnittliche Länge der roten Linie von handelt, wird das Minus weggelassen.
Mit anderen Worten, der Minus-Teil dieser Länge ...
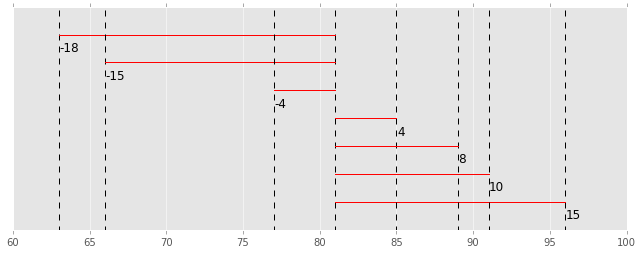 Umkehren.
Umkehren.

| ID | Absoluter Wert der Abweichung |
|---|---|
| 1 | 15 |
| 2 | 18 |
| 3 | 4 |
| 4 | 15 |
| 5 | 10 |
| 6 | 8 |
| 7 | 4 |
Der Durchschnittswert dieses "absoluten Abweichungswerts" beträgt ** 10,57 **, und dieser Wert wird als "Durchschnittsabweichung" bezeichnet. das ist,
- Durchschnittliche Entfernung vom Durchschnitt
- Indikator, wie weit vom Durchschnitt entfernt
Es gilt als. In diesem Beispiel beträgt die durchschnittliche Punktzahl 81 Punkte, die durchschnittliche Punktzahl jedoch 10,57 Punkte. Es ist keine Übertreibung zu sagen, dass dieses Konzept fast die Idee der Standardabweichung ist. Der Berechnungsansatz ist etwas anders. Wenn ich also "Standardabweichung" sage, möchte ich, dass Sie es als "Durchschnitt, wie weit vom Durchschnitt entfernt" betrachten.
Drücken Sie dies mit einer Formel aus.
Erstens das Absolutwertsymbol
Wenn es in ein Diagramm geschrieben wird, wird es so ausgedrückt und die Steigung wird invertiert, so dass der Wert in dem Bereich positiv wird, in dem $ x $ negativ ist.
 (code is here)
(code is here)
In einer mathematischen Formel ausgedrückt sieht es so aus.

Es kann interpretiert werden, dass die Abweichung durch Subtrahieren des Durchschnitts vom Wert der Daten erzeugt wird, das Minus durch Nehmen des Absolutwerts entfernt wird und der Durchschnitt genommen wird.
Im Python-Code sieht es so aus.
mean_deviation.py
x = [96, 63, 85, 66, 91, 89, 77]
ave = np.average(x)
total = 0
for i in range(len(x)):
total += abs(x[i] - ave)
print total/len(x)
</ i> 4. Standardabweichung
Schließlich die Hauptfigur dieses Artikels, "Standardabweichung". Bei "mittlerer Abweichung" wurde der Absolutwert verwendet, um Minus in Plus zu ändern, bei "Standardabweichung" wurde er quadriert und Minus genommen. Mit anderen Worten, die Idee ist genau die gleiche, nur die negative Entfernungsmethode ist unterschiedlich.
Wie unten gezeigt, besteht eine Ähnlichkeit darin, dass der Ursprung der Faltpunkt ist und symmetrisch ist und der negative Wert in positiv geändert wird.

(code is here)
(Die blaue Linie ist die Absolutwertfunktion
Im vorherigen Abschnitt wurde, wie in der folgenden Abbildung gezeigt, die Differenz zum Durchschnittswert durch die Länge der Linie ausgedrückt.

Dieses Mal besteht das Bild der Bewertung der Differenz durch das Quadrat darin, den Grad der Abweichung vom Durchschnittswert mit der Fläche des Quadrats zu bewerten, wie hier gezeigt.

Addieren wir diese Bereiche und nehmen wir den Durchschnitt.

Dies als Formel ausdrücken,

Die Summe der quadratischen Abweichungen vom Durchschnitt und vom Durchschnitt wird als "Dispersion" bezeichnet. Zu diesem Zeitpunkt ist die "Standardabweichung" nur einen Schritt entfernt.
Die am Anfang dieses Artikels gezeigte Formel wird wie folgt nachgedruckt.
\sigma = \sqrt{ {1 \over n} \sum_{i=1}^n(x_i - \bar{x})^2}
Der Unterschied zu "verteilt" besteht darin, ob die Route berechnet werden soll oder nicht. "Verteilung" ist auch ein Indikator dafür, wie viele Daten verstreut sind. Die Einheit hat sich jedoch geändert, da sie flächenmäßig berücksichtigt wird. Sie können den Bereich also wieder auf Länge bringen, indem Sie den Stamm $ \ sqrt {\ } $ verwenden.
Durch Definieren, dass die Wurzel $ \ sqrt {\ } $ der Wert im Quadrat ist, ist $ \ sqrt {9} = \ sqrt {3 ^ 2} = 3 $ oder $ \ sqrt {25} = \ sqrt Repräsentiert die Beziehung {5 ^ 2} = 5 $. Es ist die umgekehrte Berechnung von $ 3 ^ 2 = 9 $. Da $ 25 $ als die Fläche eines Quadrats von $ 5 \ times5 $ betrachtet werden kann,

Es wird so sein, wenn es in einer mathematischen Formel geschrieben wird. Berechnen Sie root $ \ sqrt {\ } $ für die gesamte Distribution. Sie können es sich als "Operation zum Extrahieren der Länge der Seite" in Bezug auf den Durchschnittswert des obigen Bereichs vorstellen.
Das heißt, die Standardabweichung ist
Standardabweichung= \sqrt{Verteilt}
Es wird.
Im Python-Code sieht es so aus.
standard_deviation.py
x = [96, 63, 85, 66, 91, 89, 77]
ave = np.average(x)
total = 0
for i in range(len(x)):
total += (x[i] - ave)**2
print np.sqrt(total/len(x))
Auch der Grund, warum ich es in "Quadrat" anstelle von "Absolutwert" geändert habe, ist etwas schwierig, aber da die Verarbeitung des für die durchschnittliche Abweichung verwendeten Absolutwerts mathematisch schwierig zu handhaben ist, habe ich ein Quadrat gewählt, das einfach zu handhaben ist. Ein Punkt ist, dass es getan wurde. Danach ist es als Distanzkonzept ziemlich natürlich, eine Route durch Quadrieren aus dem Drei-Quadrate-Theorem zu nehmen. Ich denke, das ist auch einer der Gründe.
Zusammenfassung
- Mathematische Handhabung wird bequem
- Weil das Konzept der Entfernung in erster Linie als quadratisch und geroutet definiert werden kann
Ich denke. (Eine etwas ausführlichere Erklärung wird in einem anderen Artikel gegeben: grinsen :)
</ i> 5. Beispiel 1: Mit einem Diagramm verstehen
Wie ich am Anfang gepostet habe, werde ich ein Beispiel in eine Grafik schreiben. Der Durchschnitt dieser Daten wird durch einen roten Kreis dargestellt, die Abweichung vom Durchschnitt jeder Daten wird berechnet, und die Standardabweichung wird weiter daraus berechnet und durch die Länge des roten Balkens ausgedrückt.
Es ist ein Bild, dass der Durchschnitt der Entfernung vom Durchschnittswert aller Daten die Länge dieses roten Balkens ist. Da wir dafür sorgen, dass Daten über einen größeren Bereich generiert werden, nimmt auch die Länge des Stabes mit Standardabweichung zu.
 (code is here)
(code is here)
</ i> 6. Beispiel 2: Abweichungswert
Es ist ein bekannter Abweichungswert für Universitätsprüfungen usw., aber dieser Abweichungswert basiert auch auf der "Standardabweichung".
Berechnen Sie den Durchschnitt und die Standardabweichung von den Daten aller Personen, die den Test durchgeführt haben. Und
- Personen mit einer durchschnittlichen Punktzahl haben einen Abweichungswert von 50
- Abweichungswert 60 für diejenigen, die eine Standardabweichung über dem Durchschnitt erzielt haben
- Abweichungswert 40 für diejenigen, die eine Standardabweichung unter dem Durchschnitt erzielt haben
Berechnen Sie wie folgt. Mit anderen Worten
Abweichungswert= { (Ergebnis-durchschnittlich) \über der Standardabweichung} \times 10 + 50
Es ist ein Wert, der wie folgt berechnet wird. Wenn die Punktzahl um die Länge des roten Balkens in der Grafik im vorherigen Abschnitt höher als der Durchschnitt ist, beträgt der Abweichungswert 60!
</ i> Endlich
Was haben Sie gedacht? Ich habe versucht, es so sorgfältig wie möglich zu erklären, aber als ich es neu organisierte, wurde mir wieder klar, dass es sich um ein Konzept handelt, das aus einer Vielzahl von miteinander verflochtenen Elementen besteht. Wenn ich jedoch jedes Element richtig verstehen kann, denke ich, dass ich eine allgemeine Intuition haben kann.
Ich hoffe, dass das Verständnis dieser Standardabweichung die Leute dazu bringt, "Statistiken sind interessant!" Zu denken und die Anzahl der Personen zu erhöhen, die an Datenanalyse interessiert sind!
(* Wenn es einen Teil gibt, der "Ich weiß nicht" sagt, lass es bitte im Kommentarbereich!)
Ich habe auch einen Artikel (Folie) mit dem Titel "Grundlagen der Statistik" geschrieben. Wenn Sie möchten, beziehen Sie sich bitte auf diesen Artikel. http://qiita.com/kenmatsu4/items/5a59a7375140f29b31c2
Recommended Posts