[PYTHON] Finden Sie die optimale Garreihenfolge

Thema

Lösen wir das Schedule Problem von Professor Uno vom National Institute of Informatics.

Führen Sie viele Prozesse (Suppe, gegrilltes Hähnchen, ...) so schnell wie möglich mit verschiedenen Ressourcen (Personen, Herd, Küchenmesser, Ofen) durch.

Es kann mit einem Allzwecklöser formuliert und gelöst werden, ist jedoch schwierig. Verwenden Sie daher den Nur-Planungs-Löser OptSeq. Es wird eine Gebühr erhoben, aber Sie können mit der kostenlosen Testversion bis zu Variable 15 lösen.

Informationen zur Installation und Verwendung finden Sie unter Schedule Optimization Solver OptSeq II.

Löse mit Python

Definieren Sie eine Hilfsfunktion, damit Sie den Namen nicht einzeln angeben müssen.

python

from more_itertools import pairwise
from optseq import *

def addResource(m, capacity=1, name=None, addResource_count=[0]):
    if name is None:
        addResource_count[0] += 1
        name = f'R{addResource_count[0]}'
    return m.addResource(name, capacity=capacity)
def addMode(dur, res=[], name=None, addMode_count=[0]):
    if name is None:
        addMode_count[0] += 1
        name = f'M{addMode_count[0]}'
    md = Mode(name, dur)
    for r in res:
        md.addResource(r, requirement=1)
    return md
def addActivity(m, dur, res=[], name=None, addActivity_count=[0]):
    if name is None:
        addActivity_count[0] += 1
        name = f'A{addActivity_count[0]}'
    ac = m.addActivity(name)
    md = addMode(dur, res)
    ac.addModes(md)
    return ac

Lassen Sie uns tatsächlich ein Modell erstellen und es lösen. Jede der vier Ressourcenkombinationen (Personen, Herd, Küchenzeile, Ofen) sei 1,2,4,8, damit sie durch eine einzelne Zahl dargestellt werden können. Die 5 in "'Suppe': [(5,10), ...]" bedeutet, sowohl 1 (Person) als auch 4 (Küche) zu verwenden. 10 ist die Arbeitszeit (Minuten).

python

# 1:Mann, 2:Conro, 4:Küchenmesser, 8:Ofen
prm = {'Suppe': [(5,10),(3,10),(0,20),(0,20)],
       'Yakitori': [(5,10),(9,20),(3,10)],
       'Fischgerichte': [(3,10),(9,30)],
       'Heißes Gemüse': [(5,20),(3,10)],
       'Tee': [(3,10)]} #Ressourcenflag,Zeit
m = Model() #Modell-
#Ressource
res = {i:addResource(m,j) for i,j in zip([1,2,4,8],[2,2,2,1])}
#Prozess
act = {k:[addActivity(m, d, [r for j,r in res.items() if f&j], f'{k}{i+1}')
        for i,(f,d) in enumerate(l)] for k,l in prm.items()}
for l in act.values():
    for i,j in pairwise(l):
        m.addTemporal(i,j) #In der gleichen Schüssel bestellen
m.addTemporal('sink',act['Fischgerichte'][1],'CC') # Fischgerichte2は最後に
m.addTemporal('sink',act['Tee'][0],'CC') # Tee1は最後に
m.Params.TimeLimit = 1 #Die Berechnungszeit beträgt bis zu 1 Sekunde
m.Params.Makespan = True #Minimieren Sie die Endzeit aller Prozesse
m.optimize() #Solver-Ausführung

Ergebnis

 ================ Now solving the problem ================ 
Solutions:
    source     ---     0     0
      sink     ---    70    70
Suppe 1---     0    10
Suppe 2---    10    20
Suppe 3---    20    40
Suppe 4---    40    60
Yakitori 1---     0    10
Yakitori 2---    10    30
Yakitori 3---    30    40
Fischgericht 1---    20    30
Fischgericht 2---    40    70
Heißes Gemüse 1---    30    50
Heißes Gemüse 2---    50    60
Tee 1---    60    70

Die beiden Zahlen geben die Start- und Endzeiten des Prozesses an. Da die Spüle 70 ist, können wir sehen, dass der gesamte Prozess in 70 Minuten abgeschlossen ist. Auch wenn Sie es einzeln betrachten, können Sie sehen, dass die Antwort fast das gleiche ist wie das Ergebnis des Lehrers unten.

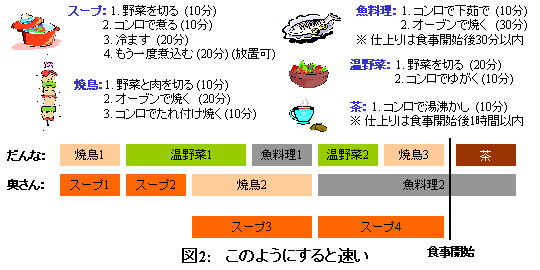
das ist alles