[PYTHON] Zusammenfassung der Aktivierungsfunktionen (Schritt, Sigmoid, ReLU, Softmax, konstante Funktion)

[Referenz] [Deep Learning von Grund auf neu](https://www.amazon.co.jp/%E3%82%BC%E3%83%AD%E3%81%8B%E3%82%89%E4% BD% 9C% E3% 82% 8BDeep-Learning-% E2% 80% 95Python% E3% 81% A7% E5% AD% A6% E3% 81% B6% E3% 83% 87% E3% 82% A3% E3 % 83% BC% E3% 83% 97% E3% 83% A9% E3% 83% BC% E3% 83% 8B% E3% 83% B3% E3% 82% B0% E3% 81% AE% E7% 90 % 86% E8% AB% 96% E3% 81% A8% E5% AE% 9F% E8% A3% 85-% E6% 96% 8E% E8% 97% A4-% E5% BA% B7% E6% AF % 85 / dp / 4873117585)

Was ist die Aktivierungsfunktion?

Die Aktivierungsfunktion bestimmt, wie die Summe der Eingangssignale aktiviert wird. Dies dient als Anordnung für die an die nächste Schicht übergebenen Werte.

In der Regel In der Aktivierungsfunktion von "einfachem Perzeptron" werden "Schrittfunktion" usw. verwendet, In der Aktivierungsfunktion von "Multilayer Perceptron (neuronales Netzwerk)" werden "Sigmoidfunktion, Softmaxfunktion" und Gleichheitsfunktion verwendet. Während diese "Schrittfunktion, Sigmoidfunktion, Softmaxfunktion" nichtlineare Funktionen genannt werden, werden Funktionen wie "y = cx" lineare Funktionen genannt. Im Allgemeinen verwenden neuronale Netze keine linearen Funktionen. Der Grund dafür ist "[Warum nicht lineare Funktionen mit mehrschichtigem Perzeptron verwenden?](Https://qiita.com/namitop/items/d3d5091c7d0ab669195f#%E3%81%AA%E3%81%9C%E5%A4%" 9A% E5% B1% A4% E3% 83% 91% E3% 83% BC% E3% 82% BB% E3% 83% 97% E3% 83% 88% E3% 83% AD% E3% 83% B3% E3% 81% A7% E7% B7% 9A% E5% BD% A2% E9% 96% A2% E6% 95% B0% E3% 82% 92% E4% BD% BF% E3% 82% 8F% E3% 81% AA% E3% 81% 84% E3% 81% AE% E3% 81% 8B) ”. Im Allgemeinen werden Softmax- und Äquivalenzfunktionen in der Ausgabeschicht verwendet.

Stufenfunktion

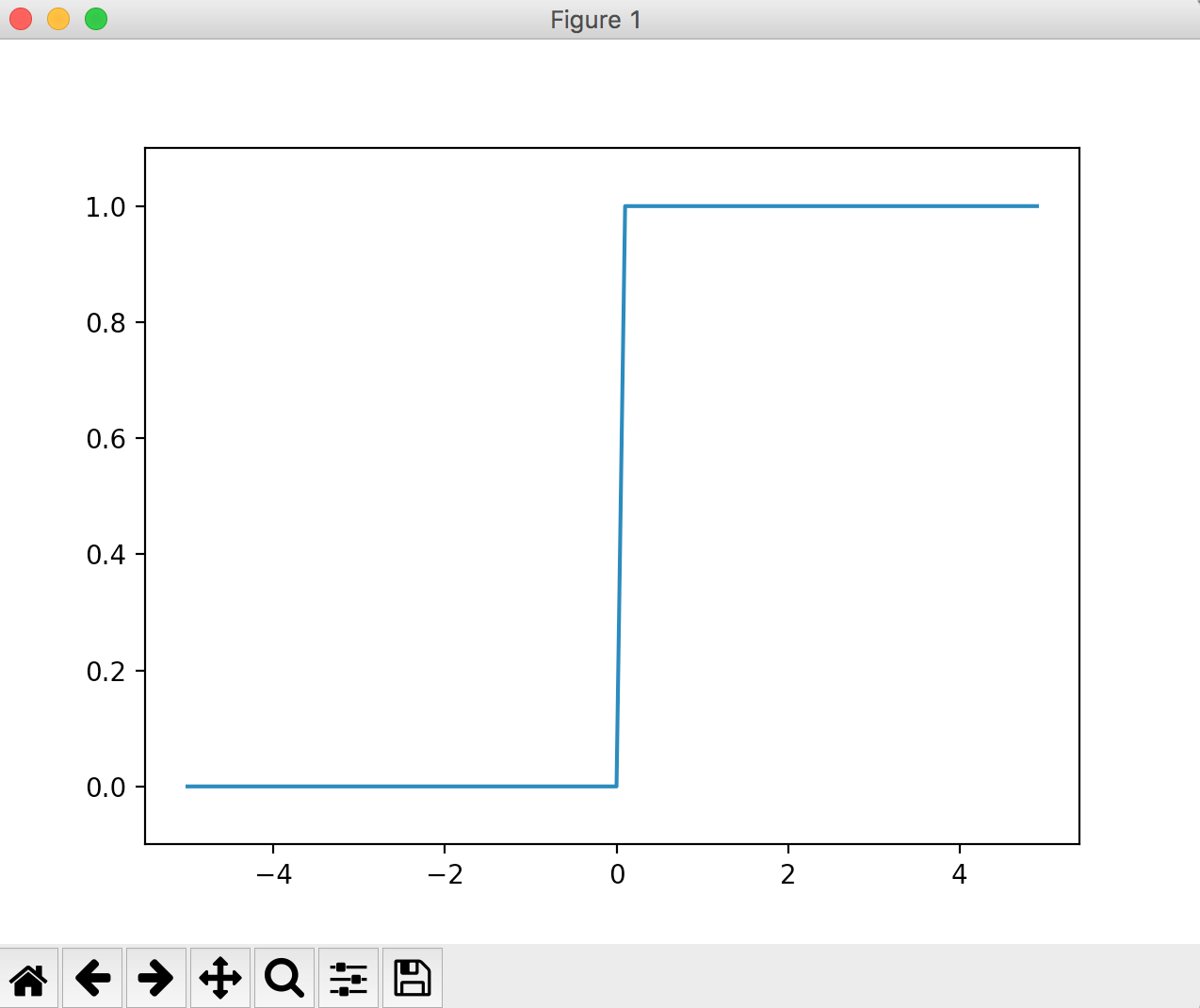
Die Schrittfunktion ist eine Funktion, die den Ausgang auf den Schwellenwert schaltet. Auch als "Treppenfunktion" bekannt. Diese Funktion wird im Allgemeinen in einfachen Perzeptronen (einschichtigen Netzwerken) verwendet.

Beispielsweise eine Sprungfunktion, die 0 wird, wenn der eingegebene Wert 0 oder kleiner ist, und 1, wenn er größer als 0 ist Die Implementierung und der Betrieb sind unten gezeigt.

def step_function(x):
  if x>0:
    return 1
  else:
    return 0

# step_function(4) => 1
# step_function(-3) => 0

Das Diagramm kann wie folgt implementiert werden. step_function ist so implementiert, dass es das Array [np.array ()] als Argument behandeln kann. Das Verhalten ist bis auf die Behandlung von Arrays dasselbe.

import numpy as np
import matplotlib.pylab as plt

def step_function(x):
  y = x > 0
  return y.astype(np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

Sigmaid-Funktion

Die Formel lautet wie folgt.

h(x) = \frac{1}{1+e^{-x}}\\
e^{-x}Ist np in numpy.exp(-x)Kann geschrieben werden.

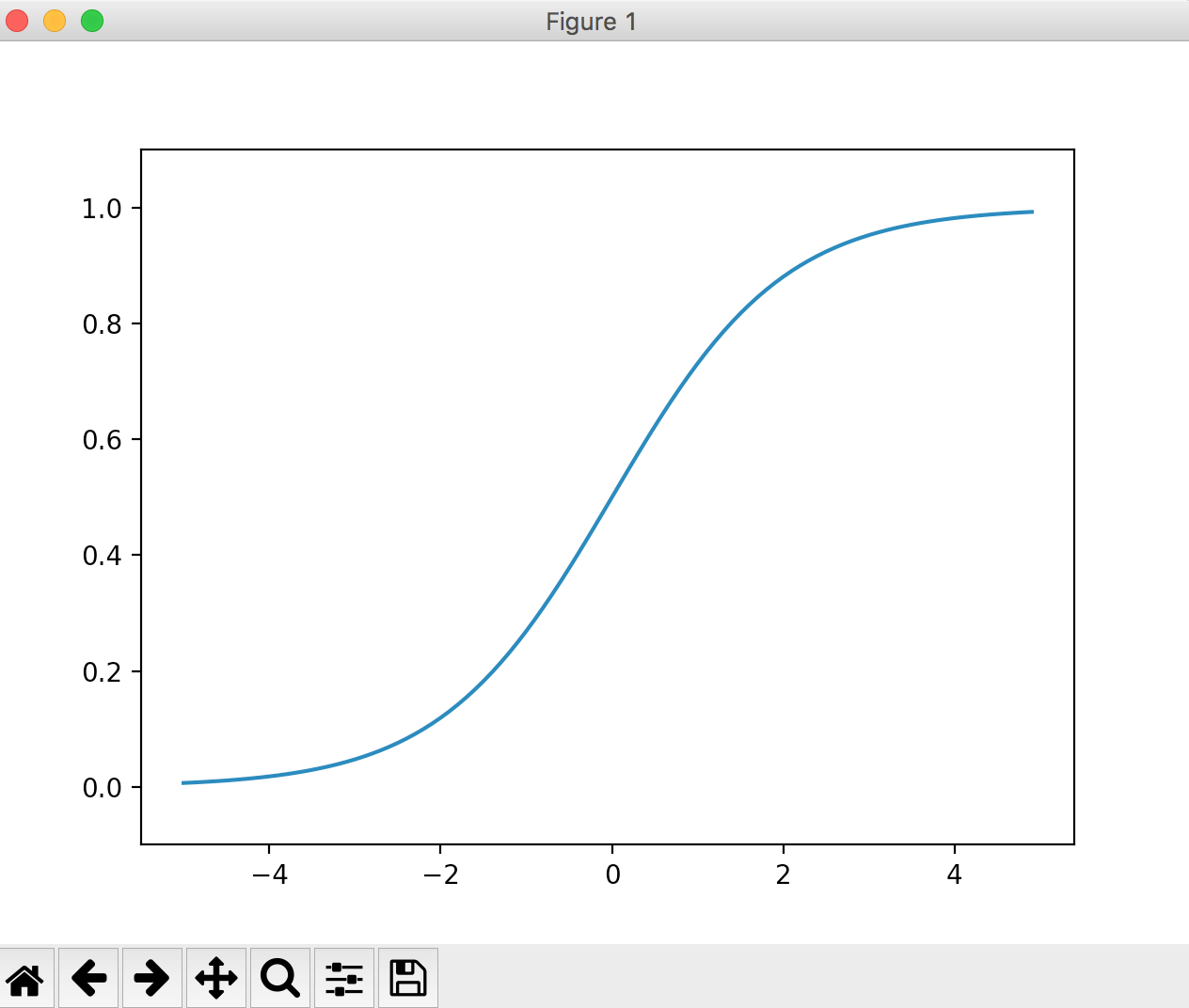
Je größer der eingegebene Wert ist, desto näher an 1 Je kleiner der eingegebene Wert ist, desto näher ist er an 0. Es kann gesagt werden, dass die Ausgabe der Schrittfunktion den Wert der ursprünglichen Eingabe im Vergleich zu 0 oder 1 nicht zu sehr zerstört.

Die Implementierung und der Betrieb sind wie folgt.

import numpy as np

def sigmoid(x):
  return 1 / (1+np.exp(-x))

x = np.array([-3.0, 1.0, 4.0])
# sigmoid(x) => [ 0.04742587  0.73105858  0.98201379]

Die Grafik sieht folgendermaßen aus:

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
  return 1 / (1+np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

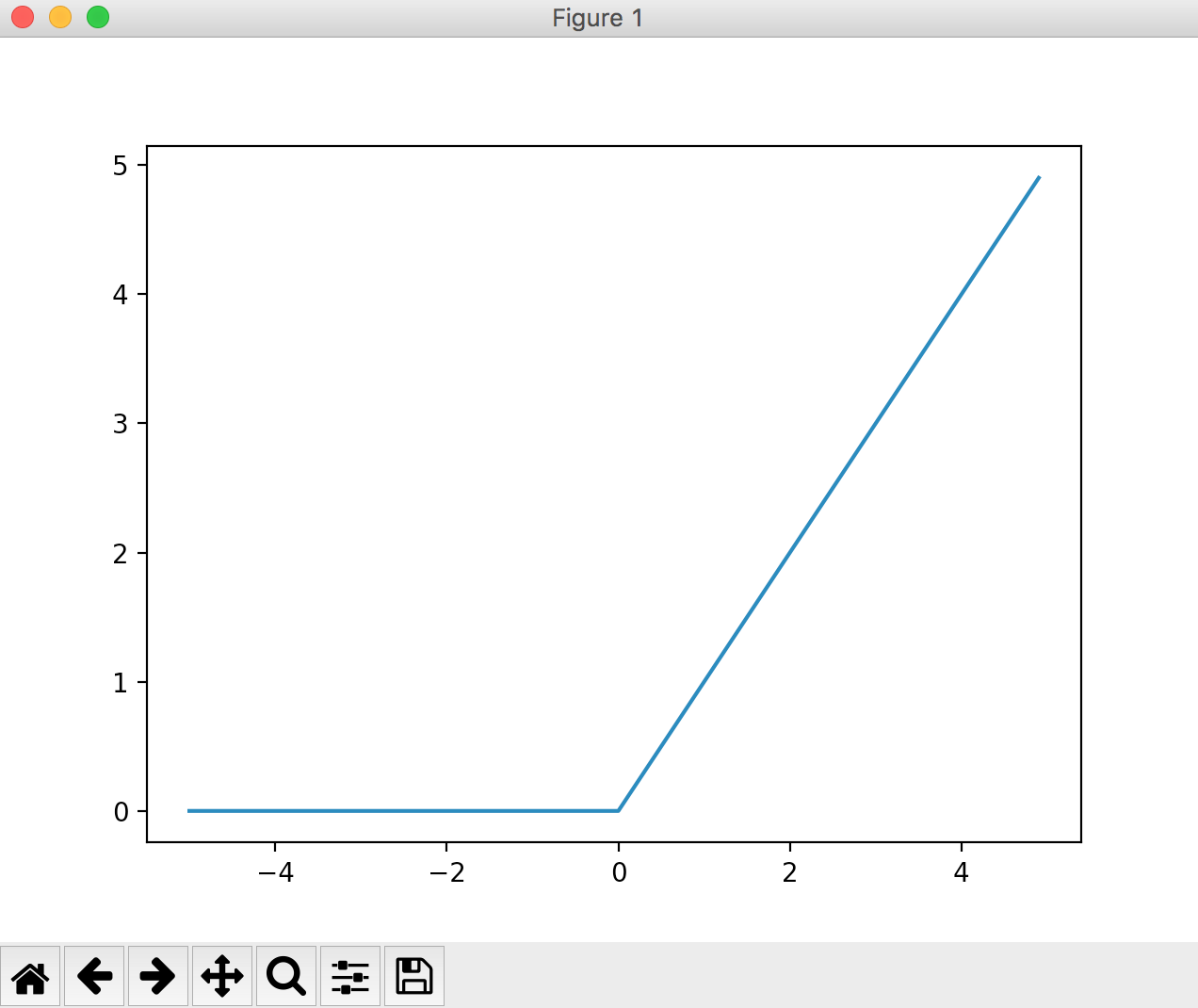
ReLU-Funktion

Wenn der Eingabewert 0 oder weniger ist, wird er 0, und wenn er größer als 1 ist, wird der Eingang so ausgegeben, wie er ist. Die Grafik sieht wie folgt aus.

import numpy as np
import matplotlib.pylab as plt

def relu(x):
  return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.show()

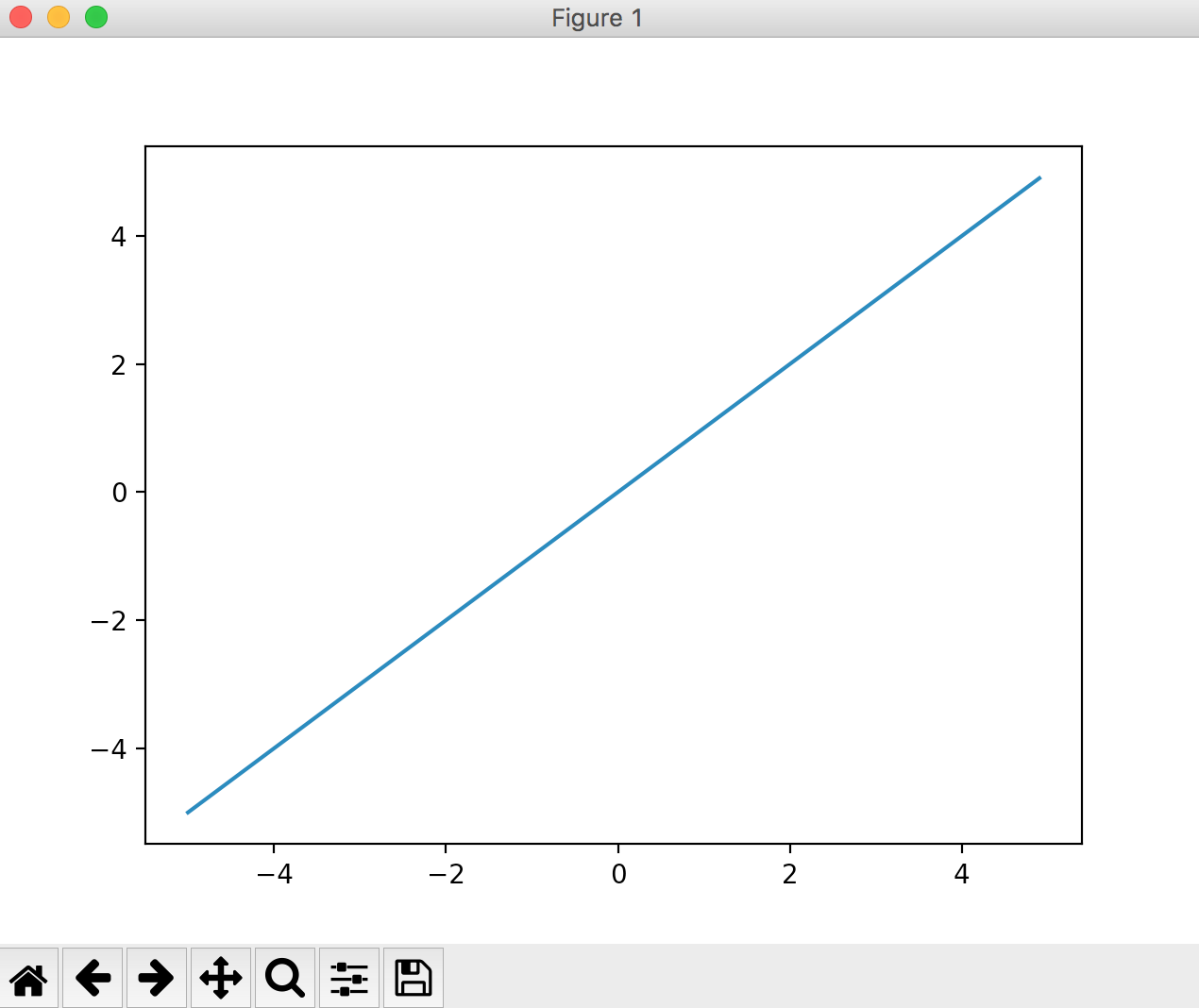
Gleiche Funktion

Eine Funktion, die in der Ausgabeebene verwendet wird. Eine Funktion, die immer den gleichen Wert wie der eingegebene Wert zurückgibt. [Frage] Mathematik: Was ist eine gleichwertige Funktion?

Wird häufig bei Regressionsproblemen verwendet.

import numpy as np
import matplotlib.pylab as plt

def koutou(a):
  return a

x = np.arange(-5, 5, 0.1)
y = koutou(x)
plt.plot(x, y)
plt.show()

Softmax-Funktion

Eine Funktion, die in der Ausgabeebene verwendet wird. Wird häufig bei Klassifizierungsproblemen verwendet.

import numpy as np
import matplotlib.pylab as plt

def softmax(a):
  exp_a = np.exp(a)
  sum_exp_a = np.sum(exp_a)
  y = exp_a / sum_exp_a
  return y

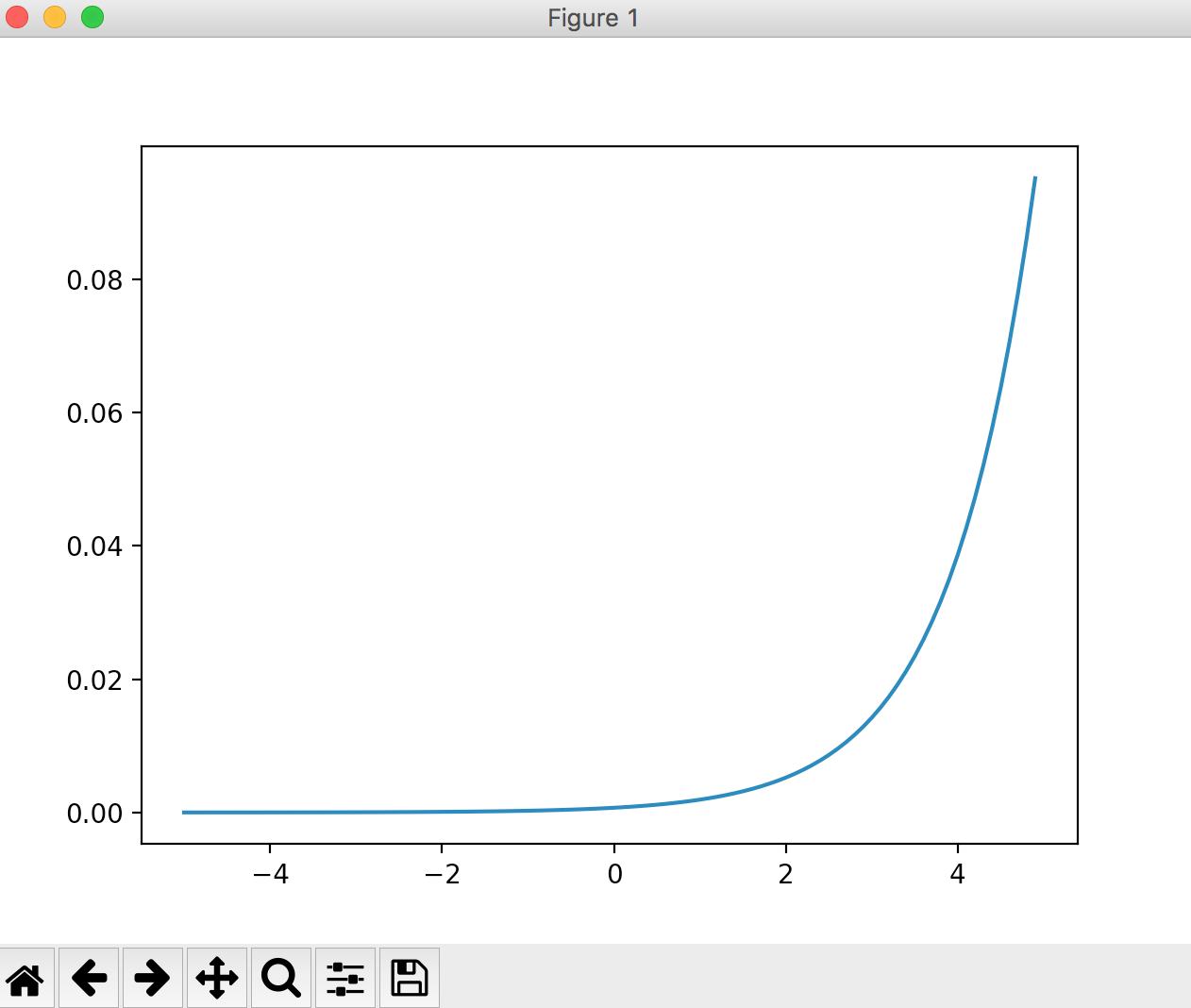
x = np.arange(-5, 5, 0.1)
y = softmax(x)
plt.plot(x, y)
plt.show()

Lineare und nichtlineare Funktionen

Eine lineare Funktion ist eine Funktion, deren Ausgabe ein konstantes Vielfaches der Eingabe ist. Zum Beispiel ist "y = cx (c ist eine Konstante)". Wenn Sie ein Diagramm erstellen, ist es eine gerade gerade Linie.

Nichtlineare Funktionen sind solche, die keine linearen Funktionen sind.

Warum nicht lineare Funktionen in mehrschichtigen Perzeptronen verwenden?

Der Grund ist, dass die Verwendung einer linearen Funktion als Aktivierungsfunktion es bedeutungslos macht, die Schicht in einem neuronalen Netzwerk zu vertiefen. Das Problem mit linearen Funktionen ist auf die Tatsache zurückzuführen, dass es unabhängig von der Tiefe der Schichten immer ein "Netzwerk ohne versteckte Schichten" gibt, das dasselbe tut. Wenn Sie als einfaches Beispiel drei Schichten mit der linearen Funktion "h (x) = cx" als Aktivierungsfunktion stapeln, erhalten Sie "y = h (h (h (x))". Das heißt, dies ist "y = c *" Es kann sogar in einem Netzwerk ohne versteckte Schicht wie c * c * x (y = ax) `ausgedrückt werden.

Wenn Sie wie in diesem Beispiel eine lineare Funktion für die Aktivierungsfunktion verwenden, können Sie nicht mehrere Ebenen nutzen. Mit anderen Worten, Sie sollten keine linearen Funktionen für Aktivierungsfunktionen verwenden, da dies zu unnötiger Verarbeitung führen kann.

Regressionsproblem und Klassifizierungsproblem

Das Regressionsproblem ist das Problem, aus einigen Eingabedaten (kontinuierliche) numerische Vorhersagen zu treffen. (Beispiel: Das Problem der Vorhersage des Gewichts einer Person anhand eines Bildes der Person)

Das Klassifizierungsproblem ist die Frage, zu welcher Klasse die Daten gehören. (Beispiel: Ein Problem, bei dem eine Person anhand eines Personenbildes als männlich oder weiblich klassifiziert wird.)