Erklären Sie die stochastische Gradientenabstiegsmethode, indem Sie sie in Python ausführen
Wofür wird die Gradientenabstiegsmethode verwendet?
Die Gradientenabstiegsmethode wird häufig in der Statistik und beim maschinellen Lernen verwendet. Insbesondere führt maschinelles Lernen häufig zur numerischen Lösung eines Problems, das einige Funktionen grundsätzlich minimiert (maximiert). (Zum Beispiel Methode der minimalen Quadrate → Minimieren Sie die Summe der Fehlerquadrate (Referenz), Bestimmen Sie die Parameter des neuronalen Netzwerks usw.)
Im Grunde ist es ein Problem, einen Ort zu finden, an dem es zu 0 und zu 0 differenziert wird. Diese Gradientenabstiegsmethode ist daher wichtig, wenn programmgesteuert gelöst werden soll, welcher Wert differenziert und zu 0 wird. Es gibt verschiedene Arten von Gradientenmethoden, aber hier werden wir uns mit der Methode mit dem steilsten Abstieg und der Methode mit dem stochastischen Gradientenabstieg befassen. Zunächst möchte ich mit einem eindimensionalen Diagramm überprüfen, um ein Bild zu erhalten.
Für eine Dimension
Bei einer Dimension gibt es kein Wahrscheinlichkeitskonzept, es handelt sich lediglich um eine Gradientenabstiegsmethode. (Was meinst du später) Verwenden wir für das eindimensionale Beispiel das Beispiel mit der Normalverteilung minus. Die Graphen von $ x_ {init} = 0 $ und $ x_ {init} = 6 $ werden als Beispiele verwendet. Der Zieldiagramm war derjenige, in dem die Dichtefunktion der Normalverteilung subtrahiert und nach unten gedreht wurde.
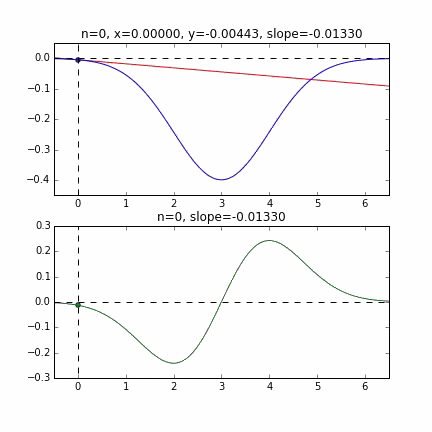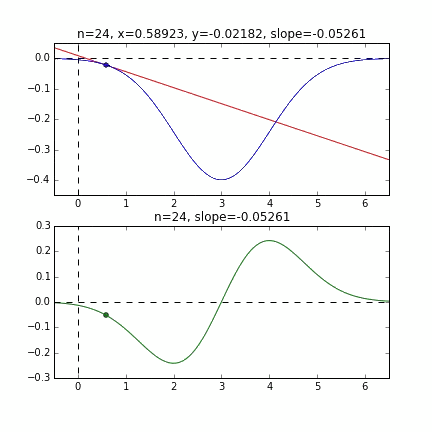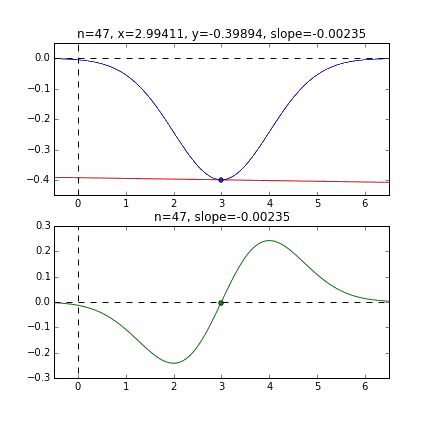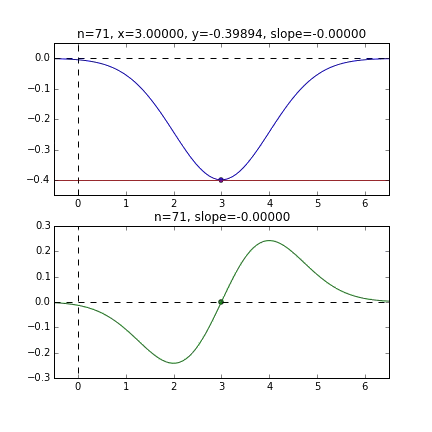
** Grafik mit Anfangswert = 0 **
Sie können sehen, dass es am Ende des Diagramms beginnt und dort, wo es am kleinsten ist, beim Minimalwert konvergiert. Das blaue Liniendiagramm ist die negative Version der Normalverteilung, und das grüne Liniendiagramm ist das Diagramm der differenzierten Werte.
** Grafik mit Anfangswert = 6 **

Bestimmen Sie den nächsten $ x $ -Wert basierend auf der Steigung an jedem Punkt, überprüfen Sie die Steigung an dieser Position und steigen Sie dann ab usw., um den Minimalwert (tatsächlich den Minimalwert) zu erreichen. Wenn sich der Wert im obigen Beispiel dem Minimalwert nähert, wird die Steigung sanft, so dass der Fortschritt in einem Schritt allmählich abnimmt und wenn er kleiner als ein bestimmter Standard wird, stoppt er. Ich werde.
Der Code, der diese beiden Diagramme geschrieben hat, lautet hier.
2D (quadratische Funktion)
Im Fall von mehrdimensional wird es unter Berücksichtigung der Richtung absteigen, um mit dem nächsten Schritt fortzufahren. Die Eigenschaften der Bewegung ändern sich abhängig von der Zielfunktion, aber zuerst habe ich einen Graphen am Beispiel der quadratischen Funktion $ Z = -3x ^ 2-5y ^ 2 + 6xy $ gezeichnet. Sie können sehen, wie es sich nach oben bewegt, während Sie sich im Zickzack bewegen.
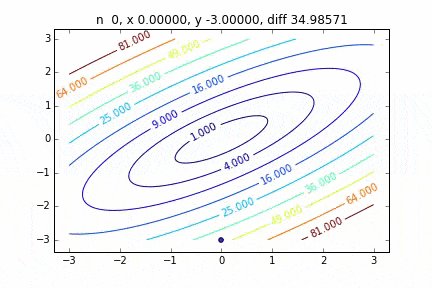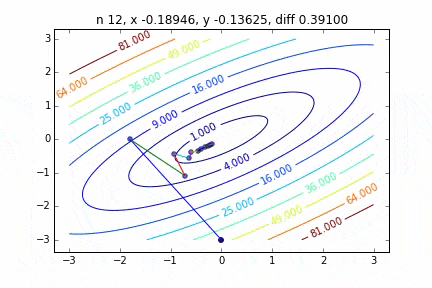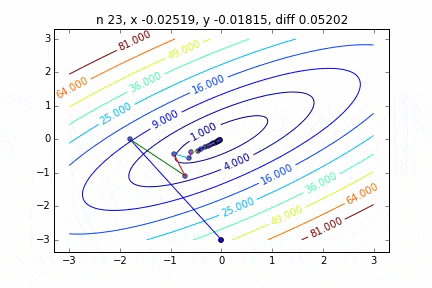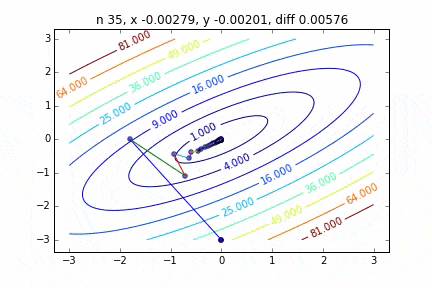
Der Code lautet hier
Für 2D
Im Fall von 2D (2D-Normalverteilung)
Es wurde festgestellt, dass sich die Methode mit dem steilsten Abstieg, wenn sie auf eine zweidimensionale Normalverteilung (Minus) angewendet wird, nicht im Zickzack bewegt und sauber auf den Minimalwert abfällt. Ich möchte den Unterschied im Konvergenzzustand in Abhängigkeit von der Zielfunktion untersuchen.

Der Code lautet hier
So funktioniert die Methode mit dem steilsten Abstieg
Der Mechanismus der Methode mit dem steilsten Abstieg besteht darin, zuerst den Startpunkt und dann den Vektor mit der größten Abstiegssteigung an diesem Punkt auszuwählen, d. H.
\nabla f = \frac{d f({\bf x})}{d {\bf x}} = \left[ \begin{array}{r} \frac{\partial f}{\partial x_1} \\ ... \\ \frac{\partial f}{\partial x_2} \end{array} \right]
Ist der Weg zum nächsten Schritt mit. In der obigen Grafik wird dieser Gradientenvektor multipliziert mit der Lernrate $ \ eta $ durch eine gerade Linie dargestellt. Damit
x_{i+1} = x_i - \eta \nabla f
Der Vorgang des Wiederholens dieses Schritts bis zur Konvergenz wird ausgeführt.
Was ist die probabilistische Gradientenabstiegsmethode?
Nun möchte ich zur stochastischen Gradientenabstiegsmethode übergehen. Zunächst möchte ich die Zielfunktion anhand der Fehlerfunktion der Regressionsgeraden erläutern, die in Erläuterung der Regressionsanalyse verwendet wird. Es gibt einen Teil, der die Interpretation ein wenig ändert (unter Verwendung der wahrscheinlichsten Methode), also Ende des Satzes Ergänzung Die Parameter der Regressionsgeraden werden nach der wahrscheinlichsten Methode als Ergänzung berechnet.
Daten sind,
y_n = \alpha x_n + \beta + \epsilon_n (\alpha=1, \beta=0)\\
\epsilon_n ∼ N(0, 2)
Nehmen wir das Beispiel der Vorbereitung von N = 1000 Datensätzen und der Ermittlung der Regressionslinie. Das Streudiagramm ist wie folgt.

Fehlerfunktion,
E({\bf w})=\sum_{n=1}^{N} E_n({\bf w}) = \sum_{n=1}^{N} (y_n -\alpha x_n - \beta)^2 \\
{\bf w} = (\alpha, \beta)^{\rm T}
Wir werden den Minimalwert von finden, aber zuerst leiten wir zur Berechnung des Gradienten den Gradientenvektor ab, der teilweise durch $ \ alpha bzw. \ beta $ differenziert ist.
\frac{\partial E({\bf w})}{\partial \alpha} = \sum_{n=1}^{N} \frac{\partial E_n({\bf w})}{\partial \alpha} =
\sum_{n=1}^N (2 x_n^2 \alpha + 2 x_n \beta - 2 x_n y_n )\\
\frac{\partial E({\bf w})}{\partial \beta} = \sum_{n=1}^{N}\frac{\partial E_n({\bf w})}{\partial \alpha} =
\sum_{n=1}^N (2\beta + 2 x_n \alpha - 2y_n)
Der Gradientenvektor ist also
\nabla E({\bf w}) = \frac{d E({\bf w}) }{d {\bf w}} = \left[ \begin{array}{r} \frac{\partial E({\bf w})}{\partial \alpha} \\ \frac{\partial E({\bf w})}{\partial \beta} \end{array} \right] = \sum_{n=1}^{N}
\nabla E_n({\bf w}) = \sum_{n=1}^{N} \left[ \begin{array}{r} \frac{\partial E_n({\bf w})}{\partial \alpha} \\ \frac{\partial E_n({\bf w})}{\partial \beta} \end{array} \right]=
\left[ \begin{array}{r}
2 x_n^2 \alpha + 2 x_n \beta - 2 x_n y_n \\
2\beta + 2 x_n \alpha - 2y_n
\end{array} \right]
Es wird sein.
Da es ein Problem ist, eine einfache Regressionslinie zu finden, kann sie als Gleichung gelöst werden, aber wir werden dies unter Verwendung der stochastischen Gradientenabstiegsmethode lösen. Anstatt hier alle Daten von N = 1000 zu verwenden, besteht der Schlüssel zu dieser Methode darin, den Gradienten für die durch Zufallsstichprobe von hier extrahierten Daten zu berechnen und den nächsten Schritt zu bestimmen.
Nehmen wir zunächst 20 zufällig aus diesem Datensatz und erstellen ein Diagramm. Die horizontale Achse ist $ \ alpha $, die vertikale Achse ist $ \ beta $ und die Z-Achse ist Fehler $ E (\ alpha, \ beta) $.

Ich denke, dass die Mindestwerte des Graphen irgendwie um $ \ alpha = 1, \ beta = 0 $ verstreut sind. Dieses Mal habe ich zufällig 3 Daten aus 1000 Daten ausgewählt und diese Grafik darauf basierend geschrieben. Der Anfangswert ist $ \ alpha = -1,5, \ beta = -1,5 $, die Lernrate ist proportional zur Umkehrung der Anzahl der Iterationen $ t $, und die Umkehrung von $ E (\ alpha, \ beta) $ an diesem Punkt wird ebenfalls multipliziert. Ich habe versucht, den einen zu benutzen. Es scheint, dass es keine andere Wahl gibt, als zu versuchen, wie man diese Lernrate und diesen Anfangswert bestimmt, aber wenn jemand einen guten Weg kennt, danach zu suchen, wäre ich dankbar, wenn Sie es mir sagen könnten. Wenn Sie einen kleinen Fehler machen, fliegen die Punkte aus dem Rahmen und kommen nicht zurück (lacht).
Da die Fehlerfunktion, die den Gradienten bestimmt, von der Zufallszahl abhängt, ist ersichtlich, dass sie sich jedes Mal ändert. Die Regressionslinie ist anfangs auch ziemlich gewalttätig, aber Sie können sehen, dass sie allmählich leiser wird und konvergiert.
 Der Code lautet hier.
Der Code lautet hier.
Um ehrlich zu sein, ist das obige Animationsbeispiel das mit der besseren Konvergenz, und die folgende Grafik zeigt die Konvergenz von $ \ alpha $ und $ \ beta $, wenn sie 10000 Mal wiederholt wird, aber $ \ alpha $ nähert sich dem wahren Wert von 1, aber $ \ beta $ konvergiert um 0,5 und es ist unwahrscheinlich, dass es sich dem wahren Wert von 0 weiter nähert.

Dies scheint diesmal auf die Eigenschaften der Fehlerfunktion der Regressionsgeraden zurückzuführen zu sein. Wie Sie jedoch aus der folgenden Grafik ersehen können, liegt die Mindestkurve für $ \ alpha $ bei $ \ alpha = 1 $. Es ist um den Wert gefallen. Da sich die vertikalen Linien jedoch nur sehr allmählich ändern, ist es schwierig, einen Gradienten zu erhalten, der vertikale Bewegungen verursacht. Wenn dies die normale Methode mit dem steilsten Abstieg usw. ist, ändert sich diese gekrümmte Oberfläche selbst nicht, daher streben wir den Mindestwert sanft entlang des Tals an, aber in erster Linie, weil sich diese gekrümmte Oberfläche jedes Mal in Richtung $ \ beta $ ändert Es scheint keine Bewegung zu geben.

Hatten Sie ein Bild der stochastischen Gradientenabstiegsmethode? Ich habe ein Bild durch Zeichnen dieses Animationsdiagramms erhalten. Der Python-Code, der die Animation dieser probabilistischen Gradientenabstiegsmethode zeichnet, finden Sie unter hier. Versuchen Sie es also, wenn Sie möchten. Bitte versuche.
(Ergänzung) Ermitteln Sie die Parameter der Regressionsgeraden mit der wahrscheinlichsten Methode
y_n = f(x_n, \alpha, \beta) + \epsilon_n (n =1,2,...,N)
Das heißt, der Fehler ist
\epsilon_n = y_n - f(x_n, \alpha, \beta) (n =1,2,...,N) \\
\epsilon_n = y_n -\alpha x_n - \beta
Kann vertreten werden durch. Wenn dieser Fehler $ \ epsilon_i $ einer Normalverteilung mit Mittelwert = 0, Varianz = $ \ sigma ^ 2 $ folgt, ist die Wahrscheinlichkeit der Fehlerfunktion
L = \prod_{n=1}^{N} \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{\epsilon_n^2}{2\sigma^2} \right)
Und wenn Sie den Logarithmus nehmen
\log L = -\frac{N}{2} \log (2\pi\sigma^2) -\frac{1}{2\sigma^2} \sum_{n=1}^{N} \epsilon_n^2
Und wenn Sie nur die Begriffe abrufen, die von den Parametern $ \ alpha, beta $ abhängen
l(\alpha, \beta) = \sum_{n=1}^{N} \epsilon_n^2 = \sum_{n=1}^{N} (y_n -\alpha x_n - \beta)^2
Sie können sehen, dass Sie minimieren sollten. Verwenden Sie dies als Fehlerfunktion
E({\bf w})=\sum_{n=1}^{N} E_n({\bf w}) = \sum_{n=1}^{N} (y_n -\alpha x_n - \beta)^2 \\
{\bf w} = (\alpha, \beta)^{\rm T}
Es wird ausgedrückt als.