1. Mit Python 2-1 gelernte Statistiken. Wahrscheinlichkeitsverteilung [diskrete Variable]
- ** Diskrete stochastische Variable ** ist eine Variable, die diskrete Werte wie Würfel annimmt, z. B. "2" nach "1", "3" nach "2" usw. In der Zwischenzeit gibt es keine fortlaufenden Zahlen wie 1.1, 1.2, 1.3, ..., 1.8, 1.9.
- Wir werden die Eigenschaften der wichtigsten ** diskreten Wahrscheinlichkeitsverteilungen ** unter Verwendung von
pmf(Wahrscheinlichkeitsmassenfunktion) undrvs(Zufallsvariablen) von scipy.stats untersuchen. Ich werde.
#Import der numerischen Berechnungsbibliothek
import numpy as np
import scipy as sp
import pandas as pd
from pandas import Series, DataFrame
#Visualisierungsbibliothek importieren
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
%matplotlib inline
#Japanisches Anzeigemodul von matplotlib
!pip install japanize-matplotlib
import japanize_matplotlib
⑴ Bernoulli-Verteilung
- Das Auftreten einer der beiden einzigen Arten von Ereignissen wird als ** Bernoulli-Versuch ** bezeichnet.
- ** Bernoulli-Verteilung ** ist die Wahrscheinlichkeitsverteilung, mit der jedes Ereignis in einem Bernoulli-Versuch auftritt.
- Wenn Sie beispielsweise 8 Mal eine Münze werfen und die Vorderseite herauskommt, ist sie 0, und wenn die Rückseite herauskommt, ist sie 1 und das Ergebnis wird wie folgt angenommen.
x = np.array([0,0,1,1,0,1,0,0])
#Berechnen Sie die Wahrscheinlichkeitsverteilung
p = len(x[x==1]) / len(x)
pmf_bernoulli = sp.stats.bernoulli.pmf(x, p)
#Visualisierung
plt.vlines(x, 0, pmf_bernoulli,
colors='blue', lw=50)
plt.xticks([0,1])
plt.xlim([0 - 0.5, 1 + 0.5])
plt.grid(True)
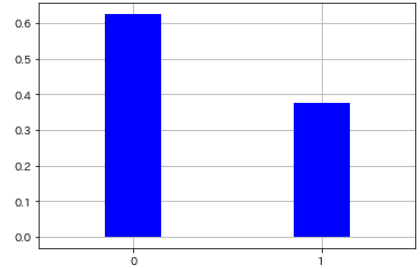
| Zwei Arten von Ereignissen | Wahrscheinlichkeit |
|---|---|
| 0 | 0.625 |
| 1 | 0.375 |
⑵ Binomialverteilung
- Die Wahrscheinlichkeitsverteilung, wie oft ein Ereignis auftritt, wenn die voneinander unabhängigen Bernoulli-Versuche n-mal wiederholt werden, wird als ** Binomialverteilung ** bezeichnet.
- Verwenden Sie beispielsweise
binom.pmf, um die Wahrscheinlichkeit zu ermitteln, mit der eine Münze mit einer Wahrscheinlichkeit p von 50% fünfmal und zwei davon erscheinen.
sp.stats.binom.pmf(n=5, p=0.5, k=2)
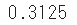
- Unter der Annahme, dass der Versuch, Münzen mit einer Wahrscheinlichkeit p von 20% zehnmal zu werfen und die Anzahl der Erscheinungen der Tabelle zu zählen, 10.000 Mal wiederholt wurde, verwenden Sie "binom.rvs", um eine Pseudozufallszahl zu generieren, die einer Binomialverteilung folgt. Machen.
- Berechnen Sie außerdem mit binom.pmf die Wahrscheinlichkeitsverteilung, wie oft die Tabelle erscheint, wenn Sie eine Münze mit einer Wahrscheinlichkeit p von 20% werfen, die zehnmal erscheint, und vergleichen Sie sie mit dem Histogramm der Pseudozufallszahlen.
#Pseudozufallszahl generieren
np.random.seed(1)
rvs_binom = sp.stats.binom.rvs(n=10, p=0.2, size=10000)
#Wahrscheinlichkeitsverteilung abrufen
m = np.arange(0, 10+1, 1)
pmf_binom = sp.stats.binom.pmf(n=10, p=0.2, k=m)
#Visualisierung
sns.distplot(rvs_binom, bins=m,
kde=False, norm_hist=True, label='rvs')
plt.plot(m, pmf_binom, label='pmf')
plt.xticks(m)
plt.legend()
plt.grid()
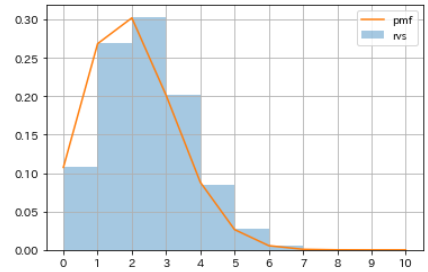
| Häufigkeit, mit der die Tabelle angezeigt wird | Wahrscheinlichkeit |
|---|---|
| 0 | 0.107374182 |
| 1 | 0.268435456 |
| 2 | 0.301989888 |
| 3 | 0.201326592 |
| 4 | 0.088080384 |
| 5 | 0.026424115 |
| 6 | 0.005505024 |
| 7 | 0.000786432 |
| 8 | 0.000073728 |
| 9 | 0.000004096 |
| 10 | 0.000000102 |
⑶ Poisson-Verteilung
- Die Wahrscheinlichkeit eines sehr seltenen Ereignisses, wie die Anzahl der Regentropfen pro Flächeneinheit oder die Anzahl der Unfälle, die an einer Kreuzung in einem Jahr auftreten, folgt der ** Poisson-Verteilung **.
- Mit anderen Worten, es ist eine Wahrscheinlichkeitsverteilung, die für eine bestimmte Zeit oder einen bestimmten Bereich mit einer konstanten Rate auftritt, und die Anzahl der Abtastwerte n ist ausreichend groß und die Wahrscheinlichkeit p ist sehr klein.
- Verwenden Sie beispielsweise "poisson.pmf", um die Wahrscheinlichkeit zu ermitteln, mit der durchschnittlich 5 Vorkommen in einem bestimmten Zeitraum nur zweimal auftreten.
sp.stats.poisson.pmf(k=2, mu=5)
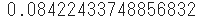
- Der Parameter der Poisson-Verteilung ist die ** durchschnittliche Anzahl von Ereignissen mu ** eines Ereignisses, die auch als ** Intensität ** oder ** λ (Lambda) ** bezeichnet wird.
- Unter der Annahme, dass die Wahrscheinlichkeit p eines Ereignisses 20% beträgt und die Häufigkeit, mit der es aufgetreten ist, 10000 Mal wiederholt wird, wird "poisson.rvs" verwendet, um eine Pseudozufallszahl zu erzeugen, die der Poisson-Verteilung folgt.
- Berechnen Sie außerdem mit
poisson.pmfdie Wahrscheinlichkeitsverteilung, wenn die Auftrittswahrscheinlichkeit p 20% beträgt, und vergleichen Sie sie mit dem Histogramm der Pseudozufallszahlen.
#Pseudozufallszahl generieren
np.random.seed(1)
rvs_poisson = sp.stats.poisson.rvs(mu=2, size=10000)
#Wahrscheinlichkeitsverteilung abrufen
m = np.arange(0, 10+1, 1)
pmf_poisson = sp.stats.poisson.pmf(mu=2, k=m)
#Visualisierung
sns.distplot(rvs_poisson, bins=m,
kde=False, norm_hist=True, label='rvs')
plt.plot(m, pmf_poisson, label='pmf')
plt.xticks(m)
plt.legend()
plt.grid()
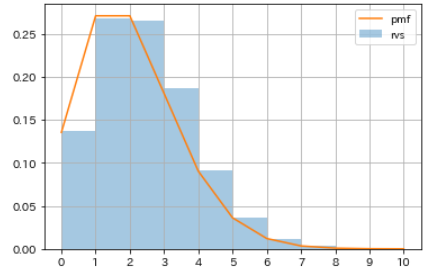
| Anzahl der Vorkommen | Wahrscheinlichkeit |
|---|---|
| 0 | 0.135335283 |
| 1 | 0.270670566 |
| 2 | 0.270670566 |
| 3 | 0.180447044 |
| 4 | 0.090223522 |
| 5 | 0.036089409 |
| 6 | 0.012029803 |
| 7 | 0.003437087 |
| 8 | 0.000859272 |
| 9 | 0.000190949 |
| 10 | 0.000038190 |
- Betrachten Sie nun die Beziehung zwischen der ** Poisson-Verteilung ** und der ** Binomialverteilung **.
- Berechnen Sie die Wahrscheinlichkeitsverteilung der ** Binomialverteilung **, wenn die Anzahl der Versuche n ausreichend groß und die Wahrscheinlichkeit p sehr klein ist, und vergleichen Sie sie mit dem vorherigen Beispiel der ** Poisson-Verteilung **.
#Geben Sie die Parameter an
n = 100000000
p = 0.00000002
#Berechnen Sie die Wahrscheinlichkeitsverteilung der Binomialverteilung
num = np.arange(0, 10+1, 1)
pmf_binom_2 = sp.stats.binom.pmf(n=n, p=p, k=num)
#Visualisierung
plt.plot(m, pmf_poisson,
color='lightgray', lw=10, label='poisson')
plt.plot(m, pmf_binom_2,
color='black', linestyle='dotted', label='binomial')
plt.xticks(num)
plt.legend()
plt.grid()
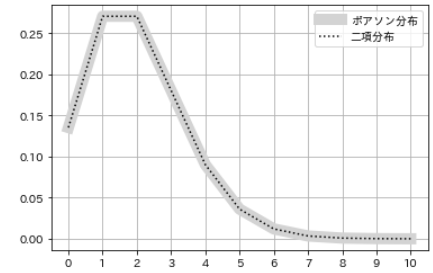
- In diesem Fall sind die ** Poisson-Verteilung ** und die ** Binomialverteilung ** nahezu gleich, was darauf hinweist, dass sie eng miteinander verbunden sind.
- ** Poisson-Verteilung ** nähert sich der Situation an, in der die Wahrscheinlichkeit des Auftretens p der ** Binomialverteilung ** sehr gering und die Anzahl der Versuche n ausreichend groß ist.
⑷ Geometrische Verteilung
- Wenn unabhängige Bernoulli-Versuche mit einer Erfolgswahrscheinlichkeit von p wiederholt werden, wird die Wahrscheinlichkeitsverteilung ** gefolgt von der Anzahl der Versuche k bis zum ersten Erfolg als ** geometrische Verteilung ** bezeichnet.
- Verwenden Sie beispielsweise "geom.pmf" in scipy.stats, um die Wahrscheinlichkeit zu ermitteln, dass nur einmal gewürfelt wird und eine "1" angezeigt wird.
%precision 3
sp.stats.geom.pmf(k=1, p=1/6)
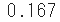
- Insgesamt gibt es 6 Würfel, und wenn alle die gleiche Wahrscheinlichkeit haben, ist es natürlich, dass 1/6 0,167 ist.
- Wirf einen nach dem anderen und finde die Wahrscheinlichkeit, dass "1" zum zweiten Mal zum ersten Mal erscheint, die Wahrscheinlichkeit, dass "1" zum ersten Mal zum dritten Mal erscheint, ... und die Wahrscheinlichkeit, dass "1" zum ersten Mal zum zehnten Mal erscheint.
#Geben Sie die Anzahl der Versuche an
num = np.arange(1, 11, 1)
#Berechnen Sie die Wahrscheinlichkeitsverteilung
prob = []
for i in num:
value = sp.stats.geom.pmf(k=i, p=1/6)
prob.append(value)
#Visualisierung
plt.bar(num, prob)
plt.xticks(num)
plt.xlabel('Häufigkeit, bis 1 zum ersten Mal erscheint')
plt.ylabel('Wahrscheinlichkeit')
plt.show()
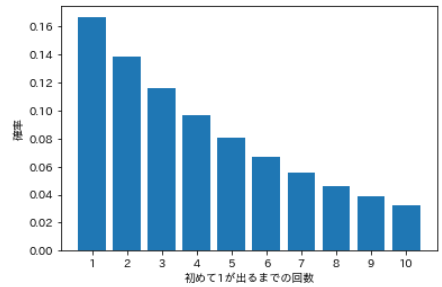
- Die Wahrscheinlichkeit, k-mal zu werfen, bis zum k-1-ten Mal zu versagen und zum k-ten Mal zum ersten Mal erfolgreich zu sein, ist in diesem Fall die Wahrscheinlichkeitsverteilung wie folgt.
| Anzahl von Versuchen | Wahrscheinlichkeit | eine Formel |
|---|---|---|
| 1 | 0.167 | ⅙ |
| 2 | 0.139 | ⅚ ・ ⅙ |
| 3 | 0.116 | ⅚ ・ ⅚ ・ ⅙ |
| 4 | 0.096 | ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
| 5 | 0.080 | ⅚ ・ ⅚ ・ ⅚ ⅚ ⅚ ⅚ ・ |
| 6 | 0.067 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ⅚ ⅚ ⅚ ・ |
| 7 | 0.056 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ・ |
| 8 | 0.047 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ⅚ ・ ⅙ |
| 9 | 0.039 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
| 10 | 0.032 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
⑸ Gleichmäßige Verteilung
- Es gibt zwei Arten der Gleichverteilung, den diskreten Typ und den kontinuierlichen Typ. Die Gleichverteilung mit diskreten Wahrscheinlichkeitsvariablen wird als ** diskrete Gleichverteilung ** bezeichnet.
- Eine Verteilung mit gleichen Wahrscheinlichkeiten aller Ereignisse, zum Beispiel Würfel folgen ** diskrete gleichmäßige Verteilung **, da alle Würfel gleiche Wahrscheinlichkeiten haben, 1 bis 6 zu würfeln.
#Geben Sie alle Ereignisse an
num = np.arange(1, 7, 1)
#Berechnen Sie die Wahrscheinlichkeitsverteilung
prob = []
for i in num:
value = 1 / len(num)
prob.append(value)
#Visualisierung
plt.bar(num, prob)
plt.xticks(num)
plt.xlabel('Augen würfeln')
plt.ylabel('Wahrscheinlichkeit')
plt.show()
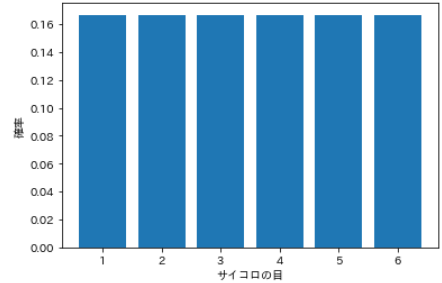
| Augen würfeln | Wahrscheinlichkeit |
|---|---|
| 1 | 0.167 |
| 2 | 0.167 |
| 3 | 0.167 |
| 4 | 0.167 |
| 5 | 0.167 |
| 6 | 0.167 |
⑹ hypergeometrische Verteilung
- Angenommen, Sie haben insgesamt 20 Lotterien, von denen 7 gewinnen. Wie viele Treffer erhalten Sie, wenn Sie zufällig 12 von 20 auswählen?
- Die Verteilung, die diese "zuzuweisende Nummer" als stochastische Variable verwendet, heißt ** supergeometrische Verteilung **.
- Es gibt drei Parameter: die Gesamtzahl M, die Zahl n pro und die Zahl N, die ausgewählt werden sollen.
#Geben Sie die Parameter an
M = 20 #Gesamtzahl
n = 7 #Anzahl der Treffer
N = 12 #Anzahl der Auswahlen
#Erstellen Sie eine stochastische Variable
k = np.arange(0, n+1)
#Erstellen Sie ein Modell
hgeom = sp.stats.hypergeom(M, n, N)
#Berechnen Sie die Wahrscheinlichkeitsverteilung
pmf_hgeom = hgeom.pmf(k)
#Visualisierung
plt.bar(k, pmf_hgeom)
plt.xticks(k)
plt.xlabel('Anzahl der Treffer')
plt.ylabel('Wahrscheinlichkeit')
plt.show()
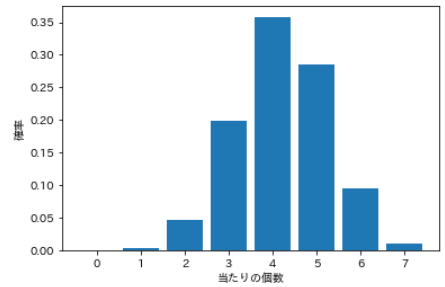
| Anzahl der Treffer | Wahrscheinlichkeit |
|---|---|
| 0 | 0.00010 |
| 1 | 0.00433 |
| 2 | 0.04768 |
| 3 | 0.19866 |
| 4 | 0.35759 |
| 5 | 0.28607 |
| 6 | 0.09536 |
| 7 | 0.01022 |
⑺ Negative Binomialverteilung
- ** Negative Binomialverteilung ** ermittelt die Erfolgswahrscheinlichkeit k-mal in n Versuchen, sofern der letzte Versuch erfolgreich ist.
- In der Binomialverteilung ist die Erfolgszahl k eine stochastische Variable, in der ** negativen Binomialverteilung ** ist die Erfolgszahl k fest. ** Verwenden Sie für die Wahrscheinlichkeitsvariable die Anzahl der Fehler n-k ** anstelle der Anzahl der Versuche n.
- Wie oft müssen Sie beispielsweise wiederholt einen Münzwurf werfen, bevor er dreimal herauskommt? Mit anderen Worten, die Anzahl der Fehler, dh wie oft sie fehlschlagen müssen, bevor sie dreimal erfolgreich sind, ist eine stochastische Variable.
#Geben Sie die Parameter an
N = 12 #Anzahl von Versuchen
p = 0.5 #Erfolgswahrscheinlichkeit
k = 3 #Anzahl der Erfolge
#Berechnen Sie die Wahrscheinlichkeitsverteilung
pmf_nbinom = sp.stats.nbinom.pmf(range(N), k, p)
#Visualisierung
plt.bar(range(N), pmf_nbinom)
plt.xlabel('Anzahl der Fehler')
plt.ylabel('Wahrscheinlichkeit')
plt.xticks(range(N))
plt.show()
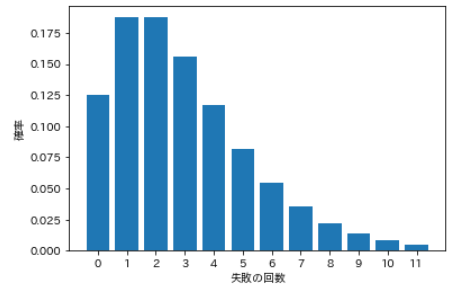
| Anzahl der Fehler | Wahrscheinlichkeit |
|---|---|
| 0 | 0.125 |
| 1 | 0.188 |
| 2 | 0.188 |
| 3 | 0.156 |
| 4 | 0.117 |
| 5 | 0.082 |
| 6 | 0.055 |
| 7 | 0.035 |
| 8 | 0.022 |
| 9 | 0.013 |
| 10 | 0.008 |
| 11 | 0.005 |
Zusammenfassung
Wir haben uns die diskrete Wahrscheinlichkeitsverteilung angesehen, werden sie jedoch in einer Liste zusammenfassen, in der bekannt ist, welche Wahrscheinlichkeitsvariable verwendet wird und was auf die x-Achse zu setzen ist.
| Arten der Wahrscheinlichkeitsverteilung | Wahrscheinlichkeitsvariable | Parameter | |
|---|---|---|---|
| ⑴ | Bernoulli-Vertrieb | Ereignis 0, 1 | Auftrittswahrscheinlichkeit p |
| ⑵ | Binäre Verteilung | Anzahl von Versuchen | Auftrittswahrscheinlichkeit p,Anzahl der Vorkommen k,Anzahl der Versuche n |
| ⑶ | Poisson-Verteilung | Anzahl von Versuchen | Durchschnittliche Anzahl der Vorkommen mu |
| ⑷ | Geometrische Verteilung | Anzahl von Versuchen | Erfolgswahrscheinlichkeit p,Anzahl der Versuche k |
| ⑸ | Diskrete Gleichverteilung | Art der Veranstaltung | ※scipy.Die gleichmäßige Verteilung der Atate ist nur ein kontinuierlicher Typ |
| ⑹ | Super geometrische Verteilung | Anzahl der Erfolge | Gesamtzahl M.,Anzahl der Erfolge im ganzen n,Anzahl der Auswahlen N. |
| ⑺ | Negative Binomialverteilung | Anzahl der Fehler | Erfolgswahrscheinlichkeit p,Anzahl der Erfolge k,Anzahl der Versuche N. |
Recommended Posts