Es gibt verschiedene Namen wie Partikelfilter / Partikelfilter und sequentielles Monte Carlo (SMC). In diesem Artikel wird jedoch der Name Partikelfilter verwendet. Ich möchte versuchen, diesen Partikelfilter in Python zu implementieren, um die latenten Variablen des Zustandsraummodells abzuschätzen.

Das Zustandsraummodell ist weiter in mehrere Modelle unterteilt, aber dieses Mal werden wir uns mit dem lokalen Modell (Differenztrendmodell erster Ordnung) befassen, das ein einfaches Modell ist. Wenn Sie wissen möchten, was noch in diesem Trendtyp des Statespace-Modells enthalten ist, klicken Sie hier (http://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.structural.UnobservedComponents.html#) Weitere Informationen finden Sie unter statsmodels.tsa.statespace.structural.UnobservedComponents).

\begin{aligned}
x_t &= x_{t-1} + v_t, \quad v_t \sim N(0, \alpha^2\sigma^2)\quad &\cdots\ {\rm System\ model} \\
y_t &= x_{t} + w_t, \quad w_t \sim N(0, \sigma^2)\quad &\cdots\ {\rm Observation\ model}
\end{aligned}

$ x_t $ repräsentiert den latenten Zustand zum Zeitpunkt t und $ y_t $ repräsentiert den beobachteten Wert.

Verwenden Sie für die zu verwendenden Daten die Beispieldaten (http://daweb.ism.ac.jp/yosoku/) von "Grundlagen der statistischen Modellierung zur Vorhersage".

Diese Testdaten können hier abgerufen werden (http://daweb.ism.ac.jp/yosoku/).

Mit dem Partikelfilter können Sie den latenten Zustand zu jedem Zeitpunkt mithilfe von Partikeln, dh Zufallszahlen, abschätzen, wie in der folgenden Grafik dargestellt. Die roten Partikel sind Partikel. Sie können filtern, indem Sie diesen Partikeln Gewichte basierend auf der Wahrscheinlichkeit zuweisen und einen gewichteten Durchschnitt verwenden. Außerdem können Sie den latenten Zustand anhand der grünen Linie schätzen. Ich werde. Wie das Beobachtungsmodell zeigt, weist der blau beobachtete Wert (derzeit verfügbare Daten) Rauschen auf, das einer Normalverteilung aus diesem latenten Zustand folgt, und [latenter Zustandswert] + [ Das Modell geht davon aus, dass [Rauschen] = [beobachteter Wert als realisierter Wert].

Im Folgenden wird ein Algorithmus beschrieben, der den Wert des latenten Zustands durch Filtern mit diesem Partikelfilter schätzt.

Klicken Sie hier für die Flow-Animation.

1. Python-Code

Die Kernklasse "ParticleFilter" ist unten. Der vollständige Code ist hier [https://github.com/matsuken92/Qiita_Contents/blob/master/particle_filter/particle_filter_class.ipynb]

class ParticleFilter(object):
    def __init__(self, y, n_particle, sigma_2, alpha_2):
        self.y = y
        self.n_particle = n_particle
        self.sigma_2 = sigma_2
        self.alpha_2 = alpha_2
        self.log_likelihood = -np.inf
    
    def norm_likelihood(self, y, x, s2):
        return (np.sqrt(2*np.pi*s2))**(-1) * np.exp(-(y-x)**2/(2*s2))

    def F_inv(self, w_cumsum, idx, u):
            if np.any(w_cumsum < u) == False:
                return 0
            k = np.max(idx[w_cumsum < u])
            return k+1
        
    def resampling(self, weights):
        w_cumsum = np.cumsum(weights)
        idx = np.asanyarray(range(self.n_particle))
        k_list = np.zeros(self.n_particle, dtype=np.int32) #Listen Sie den Speicherort der Stichprobe k auf
        
        #Lassen Sie die Indizes nach Gewicht aus der gleichmäßigen Verteilung neu abtasten
        for i, u in enumerate(rd.uniform(0, 1, size=self.n_particle)):
            k = self.F_inv(w_cumsum, idx, u)
            k_list[i] = k
        return k_list

    def resampling2(self, weights):
        """
Geschichtete Stichprobe mit weniger Berechnung
        """
        idx = np.asanyarray(range(self.n_particle))
        u0 = rd.uniform(0, 1/self.n_particle)
        u = [1/self.n_particle*i + u0 for i in range(self.n_particle)]
        w_cumsum = np.cumsum(weights)
        k = np.asanyarray([self.F_inv(w_cumsum, idx, val) for val in u])
        return k
    
    def simulate(self, seed=71):
        rd.seed(seed)

        #Anzahl der Zeitreihendaten
        T = len(self.y)
        
        #Latente Variable
        x = np.zeros((T+1, self.n_particle))
        x_resampled = np.zeros((T+1, self.n_particle))
        
        #Anfangswert der latenten Variablen
        initial_x = rd.normal(0, 1, size=self.n_particle)   #--- (1)
        x_resampled[0] = initial_x
        x[0] = initial_x

        #Gewicht
        w        = np.zeros((T, self.n_particle))
        w_normed = np.zeros((T, self.n_particle))

        l = np.zeros(T) #Haftung nach Zeit

        for t in range(T):
            print("\r calculating... t={}".format(t), end="")
            for i in range(self.n_particle):
                #Wenden Sie den Differenztrend im 1. Stock an
                v = rd.normal(0, np.sqrt(self.alpha_2*self.sigma_2)) # System Noise　#--- (2)
                x[t+1, i] = x_resampled[t, i] + v #Hinzufügen von Systemrauschen
                w[t, i] = self.norm_likelihood(self.y[t], x[t+1, i], self.sigma_2) # y[t]Haftung jedes Partikels in Bezug auf
            w_normed[t] = w[t]/np.sum(w[t]) #Standardisierung
            l[t] = np.log(np.sum(w[t])) #Jedes Mal Protokollwahrscheinlichkeit

            # Resampling
            #k = self.resampling(w_normed[t]) #Index der Partikel, die durch erneute Probenahme erhalten wurden
            k = self.resampling2(w_normed[t]) #Index der Partikel, die durch erneute Probenahme gewonnen wurden (Schichtprobenahme)
            x_resampled[t+1] = x[t+1, k]
            
        #Gesamtprotokollwahrscheinlichkeit
        self.log_likelihood = np.sum(l) - T*np.log(n_particle)
        
        self.x = x
        self.x_resampled = x_resampled
        self.w = w
        self.w_normed = w_normed
        self.l = l
        
    def get_filtered_value(self):
        """
Berechnen Sie den Wert, indem Sie nach dem gewichteten Durchschnittswert nach dem Gewicht der Wahrscheinlichkeit filtern
        """
        return np.diag(np.dot(self.w_normed, self.x[1:].T))
        
    def draw_graph(self):
        #Diagrammzeichnung
        T = len(self.y)
        
        plt.figure(figsize=(16,8))
        plt.plot(range(T), self.y)
        plt.plot(self.get_filtered_value(), "g")
        
        for t in range(T):
            plt.scatter(np.ones(self.n_particle)*t, self.x[t], color="r", s=2, alpha=0.1)
        
        plt.title("sigma^2={0}, alpha^2={1}, log likelihood={2:.3f}".format(self.sigma_2, 
                                                                                 self.alpha_2, 
                                                                                 self.log_likelihood))
        plt.show()

2. Wie der Partikelfilter funktioniert

Ich werde die Animation des Prozessablaufs erneut veröffentlichen.

Im Folgenden werde ich jeweils einen Frame erläutern.

STEP1: Es beginnt am Punkt t-1, aber wenn t = 1 ist, ist der Anfangswert erforderlich. Hier generieren wir eine Zufallszahl, die auf $ N (0, 1) $ als Anfangswert folgt, und verwenden diese als Anfangswert. Wenn t> 1 ist, entspricht das Ergebnis der vorherigen Zeit diesem $ X_ {re, t-1 | t-1} $. スライド01.png

Hier ist der Code für den Initialisierungsteil des Partikels.

initial_x = rd.normal(0, 1, size=self.n_particle)   #--- (1)

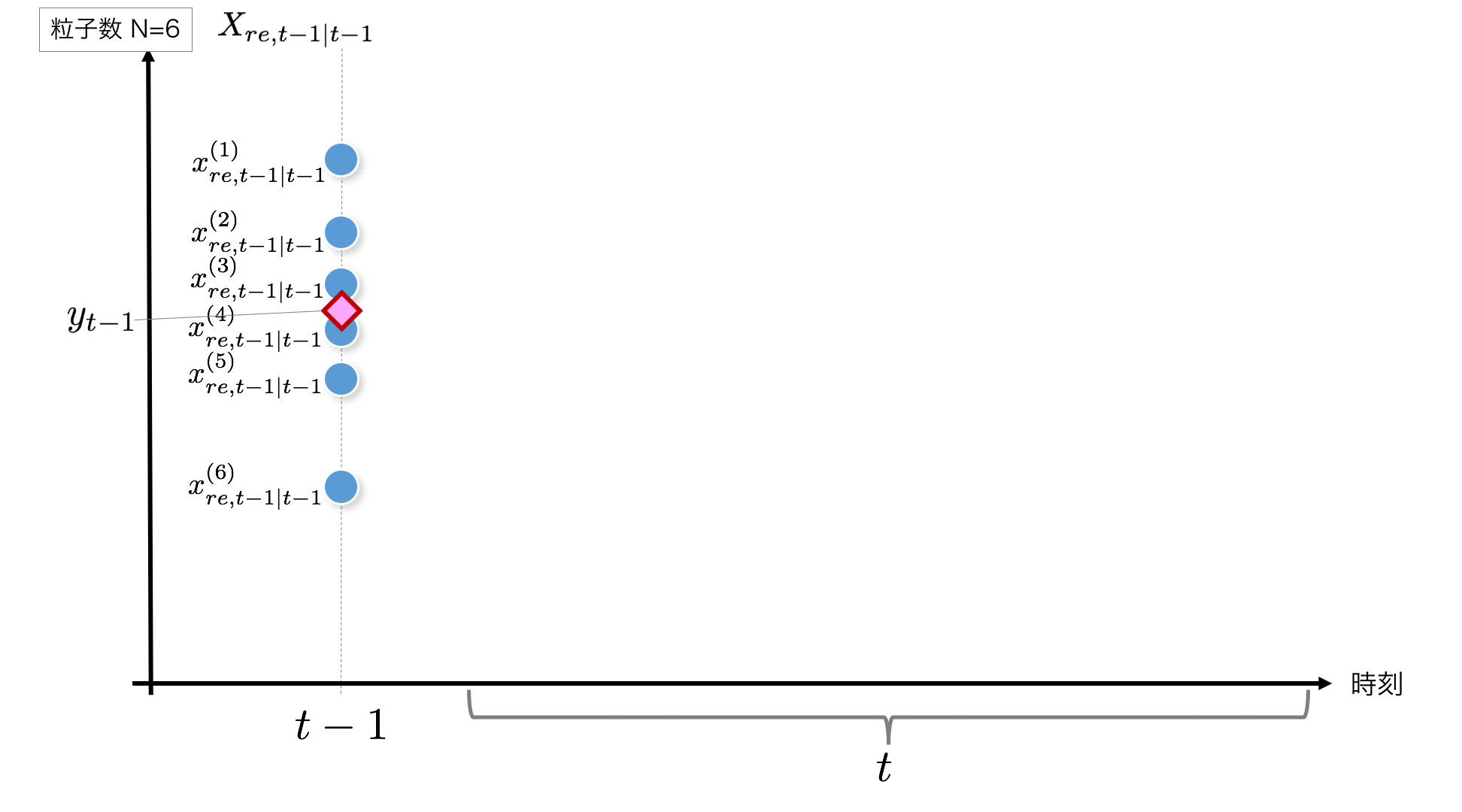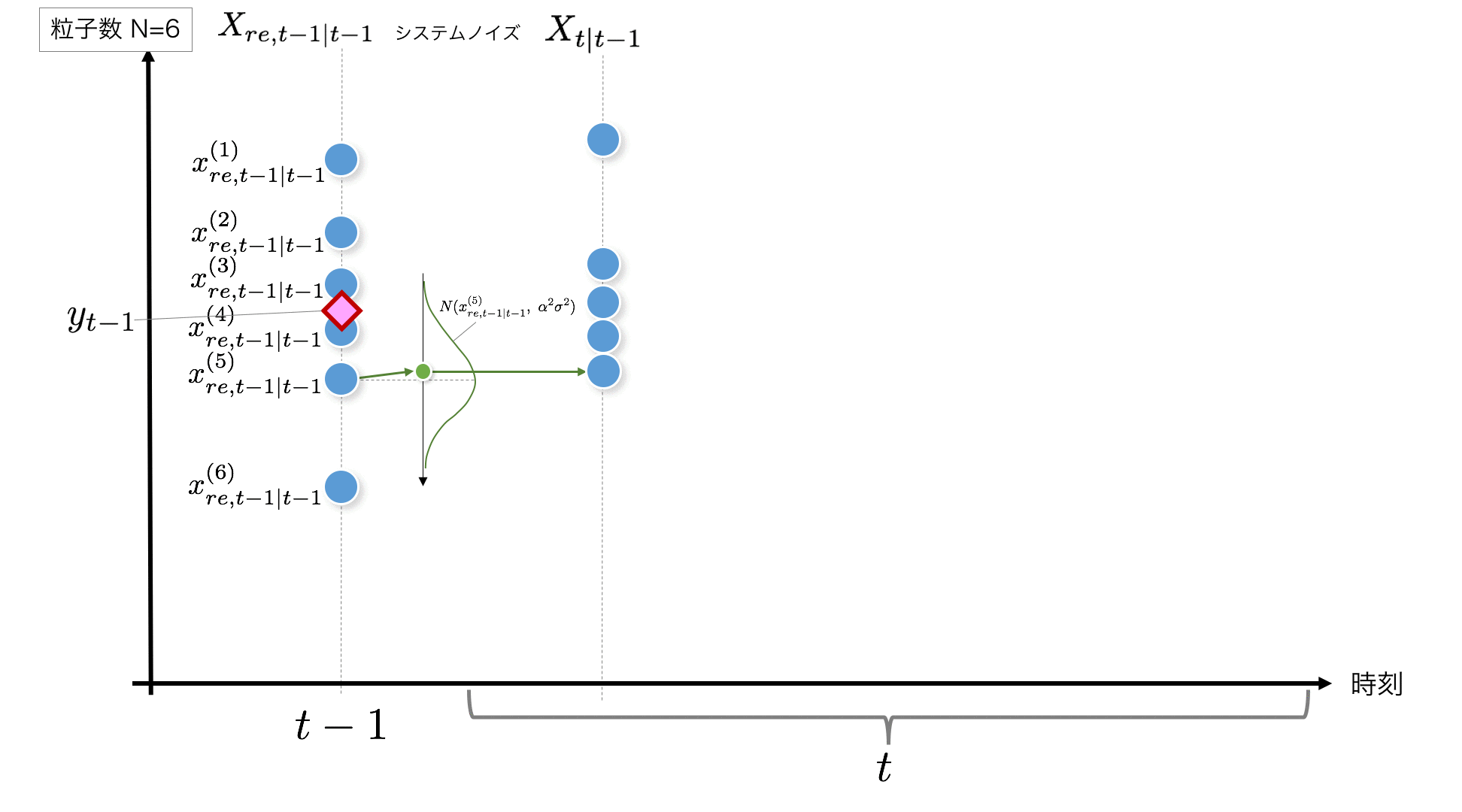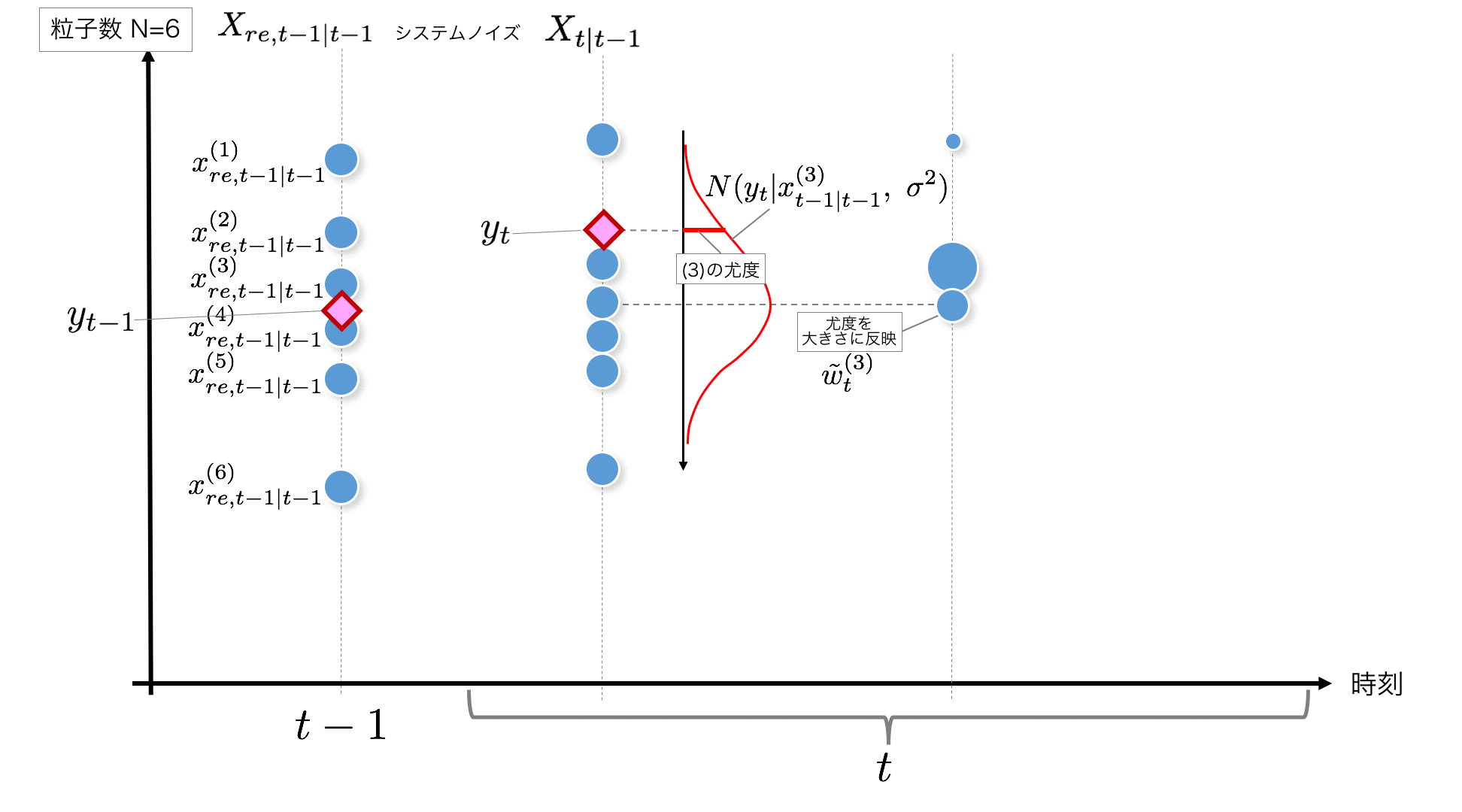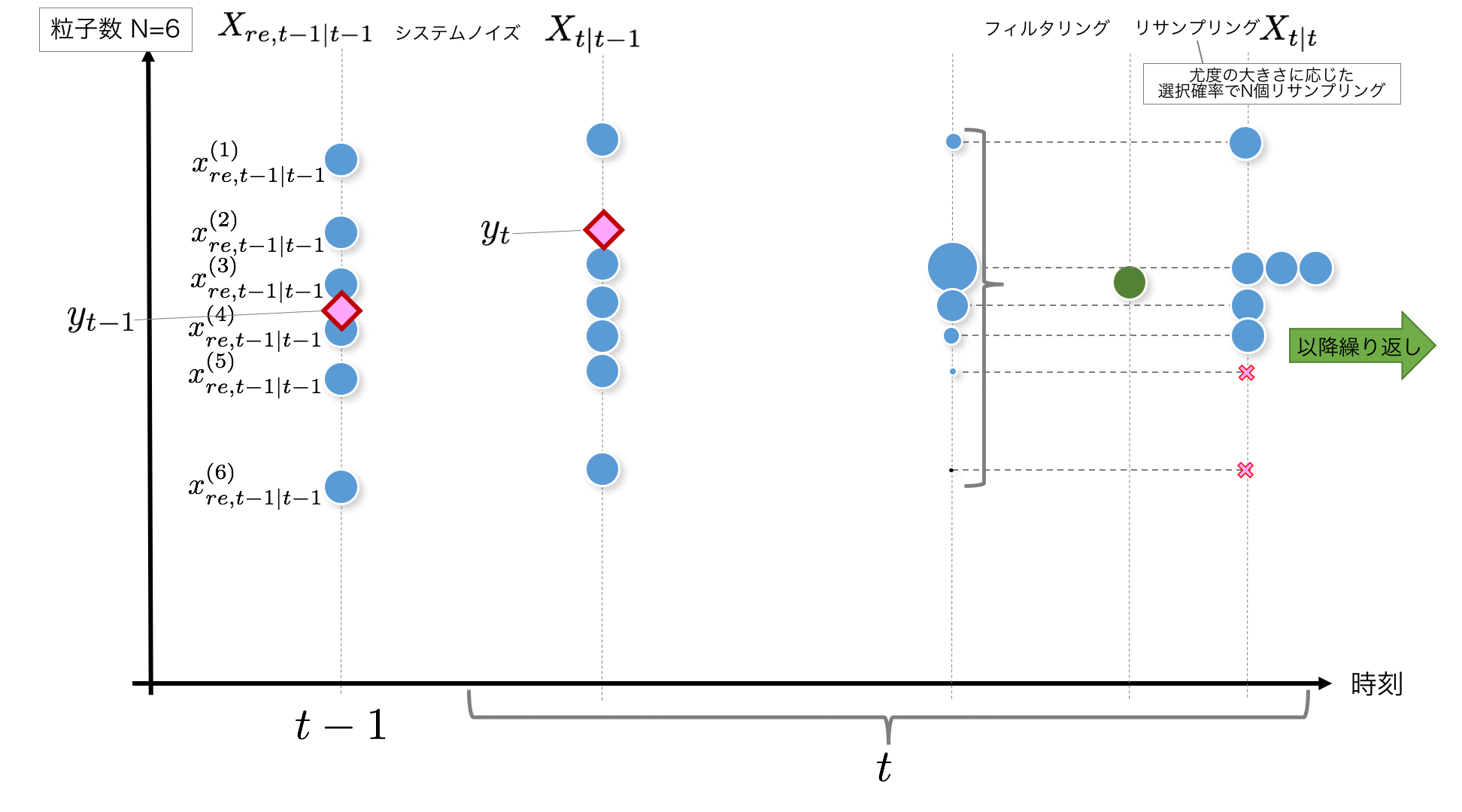
STEP2: Je nach Systemmodell wird Rauschen hinzugefügt, wenn von $ t-1 $ zum aktuellen Zeitpunkt zu $ t $ zum nächsten Mal gewechselt wird. Hier wird angenommen, dass die Normalverteilung $ N (0, \ alpha ^ 2 \ sigma ^ 2) $ befolgt wird. Tun Sie dies für die Anzahl der Partikel.

x_t = x_{t-1} + v_t, \quad v_t \sim N(0, \alpha^2\sigma^2)\quad \cdots\ {\rm System\ model}

Der Code fügt jedem Partikel Rauschen gemäß $ N (0, \ alpha ^ 2 \ sigma ^ 2) $ hinzu, wie unten gezeigt.

v = rd.normal(0, np.sqrt(self.alpha_2*self.sigma_2)) # System Noise　#--- (2)
x[t+1, i] = x_resampled[t, i] + v #Hinzufügen von Systemrauschen

STEP3: Nachdem alle Partikelwerte $ x_ {t | t-1} $ nach dem Hinzufügen des Rauschens $ y_t $, der zum Zeitpunkt $ t $ beobachtete Wert ist, erhalten werden, wird die Wahrscheinlichkeit jedes Partikels berechnet. Machen. Die hier berechnete Wahrscheinlichkeit ist die wahrscheinlichste des Partikels für den gerade erhaltenen beobachteten Wert $ y_t $. Ich möchte dies als Gewicht des Partikels verwenden, also setze ich es in eine Variable und speichere es. Diese Wahrscheinlichkeitsberechnung wird auch für die Anzahl der Partikel durchgeführt.

Die Wahrscheinlichkeit ist

p(y_t|x_{t|t-1}^{(i)}) = w_{t}^{(i)} = {1 \over \sqrt{2\pi\sigma^2}} \exp \left\{
-{1 \over 2} {(y_t - x_{t|t-1}^{(i)})^2 \over \sigma^2}
\right\}

Berechnen mit. Nach Berechnung der Wahrscheinlichkeit für alle Partikel werden die normalisierten Gewichte (zu 1 addiert)

\tilde{w}^{(i)}_t = { w^{(i)}_t \over \sum_{i=1}^N w^{(i)}_t}

Bereiten Sie auch vor.

def norm_likelihood(self, y, x, s2):
    return (np.sqrt(2*np.pi*s2))**(-1) * np.exp(-(y-x)**2/(2*s2))

w[t, i] = self.norm_likelihood(self.y[t], x[t+1, i], self.sigma_2) # y[t]Haftung jedes Partikels in Bezug auf
w_normed[t] = w[t]/np.sum(w[t]) #Standardisierung

STEP4: Gewichteter Durchschnitt unter Verwendung des zuvor gespeicherten Gewichts $ \ tilde {w} ^ {(i)} _t $

\sum_{i=1}^N \tilde{w}^{(i)}_t x_{t|t-1}^{(i)}

Wird als gefilterter $ x $ -Wert berechnet.

Im Code gilt der folgende "get_filtered_value ()".

def get_filtered_value(self):
    """
Berechnen Sie den Wert, indem Sie nach dem gewichteten Durchschnittswert nach dem Gewicht der Wahrscheinlichkeit filtern
    """
    return np.diag(np.dot(self.w_normed, self.x[1:].T))

STEP5: Unter Berücksichtigung des Gewichts $ \ tilde {w} ^ {(i)} _t $ basierend auf der Wahrscheinlichkeit als der Wahrscheinlichkeit, extrahiert zu werden,

X_{t|t-1}=\{x_{t|t-1}^{(i)}\}_{i=1}^N

N-Stücke aus erneut abtasten. Dies wird als Resampling bezeichnet, ist jedoch ein Bild einer Operation, bei der Partikel mit geringer Wahrscheinlichkeit eliminiert und Partikel mit hoher Wahrscheinlichkeit in mehrere Teile aufgeteilt werden.

k = self.resampling2(w_normed[t]) #Index der durch Resampling (Layered Sampling) gewonnenen Partikel
x_resampled[t+1] = x[t+1, k]

Erstellen Sie beim Resampling eine empirische Verteilungsfunktion aus $ \ tilde {w} ^ {(i)} _t $, wie unten gezeigt, und erstellen Sie die Umkehrfunktion, um den Bereich von (0,1] einheitlich zu machen. Jedes Teilchen kann mit einer Wahrscheinlichkeit entsprechend dem Gewicht aus einer Zufallszahl extrahiert werden.

F_inv () ist der Code, der die Umkehrfunktion verarbeitet, und resampling2 () ist der Code, der eine geschichtete Abtastung durchführt. Die geschichtete Abtastung wird unter Bezugnahme auf "Kalman Filter-Time Series Prediction und State Space Model Using R- (Statistics One Point 2)" implementiert.

\begin{aligned}
u &\sim U(0, 1) \\
k_i &= F^{-1}((i-1+u)/N) \quad i=1,2,\cdots, N \\
x^{(i)}_{t|t} &= x^{(k_i)}_{t|t-1}
\end{aligned}

Es ist wie es ist. Anstatt N einheitliche Zufallszahlen zwischen (0, 1] zu generieren, generieren Sie nur eine einheitliche Zufallszahl zwischen (0, 1 / N] und 1 / N zwischen (0, 1]). Es wird angenommen, dass N Stücke mit einer gleichmäßigen Breite abgetastet werden, indem sie einzeln verschoben werden.

def F_inv(self, w_cumsum, idx, u):
        if np.any(w_cumsum < u) == False:
            return 0
        k = np.max(idx[w_cumsum < u])
        return k+1

def resampling2(self, weights):
    """
Geschichtete Stichprobe mit weniger Berechnung
    """
    idx = np.asanyarray(range(self.n_particle))
    u0 = rd.uniform(0, 1/self.n_particle)
    u = [1/self.n_particle*i + u0 for i in range(self.n_particle)]
    w_cumsum = np.cumsum(weights)
    k = np.asanyarray([self.F_inv(w_cumsum, idx, val) for val in u])
    return k

Durch Ausführen dieser Operation von t = 1 bis T können Partikel erzeugt und gefiltert werden.

Das Ergebnis ist die folgende Grafik.

3. Stellen Sie sicher, dass die Implementierung korrekt ist, indem Sie sie mit den Ergebnissen des Kalman-Filters vergleichen

Jetzt möchte ich überprüfen, ob sich der implementierte Partikelfilter korrekt verhält oder ob er dasselbe Ergebnis ausgibt, indem ich ihn für alle Fälle mit dem Ergebnis des Kalman-Filters in Stats Models vergleiche. Ich denke

# Unobserved Components Modeling (via Kalman Filter)Hinrichtung von
import statsmodels.api as sm

# Fit a local level model
mod_ll = sm.tsa.UnobservedComponents(df.data.values, 'local level')
res_ll = mod_ll.fit()

print(res_ll.summary())

# Show a plot of the estimated level and trend component series
fig_ll = res_ll.plot_components(legend_loc="upper left", figsize=(12,8))
plt.tight_layout()

Wenn Sie dies mit dem Ergebnis des Partikelfilters überlagern, ist es fast genau das gleiche! : lacht:

Dies ist die Implementierung des Partikelfilters. Die Erklärung, warum dies funktioniert, ist ein Muss, da Tomoyuki Higuchi (Autor), die Grundlagen der statistischen Modellierung für die Vorhersage, sehr leicht zu verstehen ist.

Hausaufgaben

Hinzufügen eines Konfidenzintervalls zu jedem Zeitpunkt
Vorhersage nach T.
Ich habe noch keine feste Stollenglättung hinzugefügt, daher möchte ich sie hinzufügen.
Die Hyperparametersuche ist mit der Rastersuche nicht gut, daher möchte ich darüber nachdenken.
Unterstützt andere Trends als lokale Modelle und das Hinzufügen von saisonalen Begriffen
Beschleunigen

Referenz

Auf dieser Seite verwendeter Code https://github.com/matsuken92/Qiita_Contents/blob/master/particle_filter/particle_filter_class.ipynb
Grundlagen der statistischen Modellierung zur Vorhersage Tomoyuki Higuchi (Autor) https://www.amazon.co.jp/dp/4061557955
Kalman Filter-Zeitreihen-Vorhersage und Zustandsraummodell unter Verwendung von R- (Statistik One Point 2) Shunichi Nomura (Autor) https://www.amazon.co.jp/dp/4320112539
Computerstatistik 2 Markov-Kette Monte-Carlo-Methode und ihre Umgebung (Grenze der statistischen Wissenschaft 12) Yukito Iba (Autor), Masami Tanemura (Autor) https://www.amazon.co.jp/dp/4000068520
StatsModels: Unobserved Components Modeling
http://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.structural.UnobservedComponents.html#statsmodels.tsa.statespace.structural.UnobservedComponents

Implementierung des Partikelfilters durch Python und Anwendung auf das Zustandsraummodell

1. Python-Code

2. Wie der Partikelfilter funktioniert

3. Stellen Sie sicher, dass die Implementierung korrekt ist, indem Sie sie mit den Ergebnissen des Kalman-Filters vergleichen

Hausaufgaben

Referenz