[PYTHON] Variational Autoencoder Gründliche Erklärung
In diesem Artikel wird eines der Deep-Learning-Modelle vorgestellt, der Variational Autoencoder (VAE). Ich versuche, Chainer als Deep-Learning-Framework zu verwenden.
Mit VAE können Sie solche Bilder erstellen. VAE ist eines der Generierungsmodelle durch tiefes Lernen, und es ist möglich, Daten zu generieren, die dem Trainingsdatensatz ähnlich sind, indem seine Eigenschaften basierend auf den Trainingsdaten erfasst werden. Unten finden Sie eine animierte Version der von VAE generierten Daten. Bitte lesen Sie den Text für Details.

Der in diesem Artikel vorgestellte Python-Code finden Sie unter hier.
1. Was ist ein Variations-Autoencoder?
Zunächst möchte ich erklären, was VAE ist, aber vorher möchte ich einen normalen Auto-Encoder ansprechen.
1-1. Normaler Auto-Encoder
Was ist ein Auto-Encoder?
- Eines des unbeaufsichtigten Lernens. Daher sind die Eingabedaten zum Zeitpunkt des Lernens nur Trainingsdaten, keine Lehrerdaten.
- Ein neuronales Netzwerk zum Erfassen von Funktionen, die Daten darstellen.
Es hat solche Eigenschaften. Am Beispiel von MNIST handelt es sich um ein neuronales Netzwerk, das ein Bild mit 28 x 28 Zahlen erstellt und dasselbe Bild ausgibt. Es ist ein Bild der folgenden Abbildung. Das neuronale Netzwerk, das die Eingabedaten $ X $ in die latente Variable $ z $ konvertiert, heißt Encoder. (Es wird als Encoder bezeichnet, da die Eingabedaten als codiert angesehen werden können.) Wenn zu diesem Zeitpunkt die Dimension von $ z $ kleiner als die Eingabe $ X $ ist, kann sie auch als Dimensionsreduzierung angesehen werden. Umgekehrt wird ein neuronales Netzwerk, das das Originalbild unter Verwendung der latenten Variablen $ z $ als Eingabe wiederherstellt, als Decoder bezeichnet.

Wenn der Fall, in dem das neuronale Netz eine Schicht hat, durch eine mathematische Formel ausgedrückt wird,
\hat{x}(x) = \hat{f}(\hat{W} f(Wx+b)+\hat{b})
ist. Verlust zu diesem Zeitpunkt
Loss = \sum_{n=1}^N \|x_n - \hat{x}(x_n) \|^2
Wird besorgt. Dies wird als Rekonstruktionsfehler bezeichnet. Dies kann durch Aktualisieren der Gewichte durch das Fehlerrückverteilungsverfahren gelernt werden, so dass es so nah wie möglich an den Eingabedaten liegt.
1-2. Variational Autoencoder(VAE)
Der große Unterschied besteht darin, dass VAE eine Wahrscheinlichkeitsverteilung für diese latente Variable $ z $ annimmt, normalerweise $ z \ sim N (0, 1) $. Mit einem normalen Auto-Encoder schiebe ich Daten in die latente Variable $ z $, bin mir aber nicht sicher, wie die Struktur ist. VAE ermöglicht es, die latente Variable $ z $ in eine Struktur zu verschieben, die als Wahrscheinlichkeitsverteilung bezeichnet wird.
Das Bild ist unten.

Ich bin noch nicht sicher. Wenn Sie sich ansehen, was Sie tatsächlich ausführen, erhalten Sie ein kleines Bild.
Vergleichen wir zunächst die Ein- und Ausgabe. (Dies wurde gelernt, indem die Dimension von $ z $ auf 20 gesetzt wurde.) Es ist etwas vage, aber die ursprüngliche Form ist fast wiederhergestellt. Da es sich bei MNIST ursprünglich um 784-dimensionale Daten handelt, kann gesagt werden, dass die meisten wesentlichen Merkmale in die 20-dimensionale reduzierte Dimension integriert werden könnten.

Als nächstes sehen wir das Verhalten nur im Encoder-Teil. Angenommen, es gibt einen Encoder, der bereits trainiert wurde, fügen Sie einen Datensatz mit Trainingsdaten ein und legen Sie ihn in einer latenten Variablen ab. Machen Sie die $ z $ -Dimension zweidimensional, damit sie visualisiert werden kann. Sie können sehen, dass der MNIST-Datensatz der Trainingsdaten auf einem Kreis verstreut ist, der einer zweidimensionalen Normalverteilung folgt. Auch wenn dies ein Miso ist, kann man sehen, dass Daten mit derselben Klassenbezeichnung trotz unbeaufsichtigten Lernens ohne Lehrerdaten in unmittelbarer Nähe gesammelt werden. Dies liegt daran, dass VAE so konzipiert ist, dass $ z $ einer Normalverteilung folgt und Zufallszahlen enthält, die der Normalverteilung während des Lernens folgen. Diese zufällige Unschärfe bewirkt also, dass ähnliche Formen näher zusammenrücken. Mit anderen Worten, selbst wenn Sie dasselbe Bild eingeben, wird $ z $ jedes Mal an einer etwas anderen Position gezeichnet, und das von Decoder aus diesem $ z $ erzeugte Bild entspricht dem Eingabebild. Die Position, an der die Zahlen im Streudiagramm unten im Text dargestellt sind, befindet sich in der Mitte jedes Etiketts.

Was ist nun, wenn wir versuchen, Daten zu generieren, indem wir die Daten entlang des Raums der latenten Variablen schrittweise von "0" auf "7" verschieben?

Die folgende Animation ist das Ergebnis.
t\cdot z_0 + (1-t)\cdot z_7, \ \ 0\leq t \leq 1
Das MNIST-Bild wird vom Decoder generiert, wobei $ t $ nach und nach als Eingabe von 0 auf 1 verschoben wird. Sie können sehen, wie es bei 0 beginnt und die Zahlen zwischen 0-6-2-8-9-4-7 und 7 durchläuft: Augenzwinkern: Dies sind N (0), nicht die Trainingsdaten selbst. , 1) Das Miso ist, dass das Bild von der oben abgebildeten VAE erzeugt wird.

Unten sehen Sie eine Anzeige jedes Frames.

Die folgende Abbildung zeigt das entsprechende Ausgabebild, indem $ -2 \ leq z_1 \ leq 2, \ -2 \ leq z_2 \ leq 2 $ aus dem zweidimensionalen Raum von $ z $ ausgeschnitten und in den Decoder eingegeben werden. Werden. Die rote Linie ist die Flugbahn der vorherigen Bewegung.

Aus den Trainingsdaten ist ersichtlich, dass die Positionsbeziehung fast dieselbe ist wie die von Encoder generierte $ z $ -Karte. Im Gegensatz dazu ist der Ort, an dem die Wahrscheinlichkeit (Dichte) vom Standpunkt von N (0, 1) sehr gering ist, weit vom ursprünglichen Datensatz entfernt, so dass das entsprechend erzeugte Bild in Form von Zahlen gebrochen wird. Man kann sagen, dass dies die Struktur der Wahrscheinlichkeitsverteilung der Datenerzeugung korrekt darstellt.

Es ist ein Diagramm, das alle Situationen zeigt, die von 0 bis 9 beginnen und jeweils 0 bis 9 erreichen. In diesem Beispiel wird die Dimension der latenten Variablen auf 20 erhöht. Anders als zuvor sind also weniger Nummern unterwegs. Da die Dimension hoch ist, hat sich die Ausdruckskraft verbessert.

1-3. Diversitätshypothese
Eines der Merkmale von Deep Learning ist, dass Sie Aufgabenlernen und Ausdruckslernen kombinieren können. Hochdimensionale Daten wie Bilder werden tatsächlich nur in einem kleinen Teil der hochdimensionalen Daten verteilt, und aussagekräftige Daten (Daten, die die Essenz von Trainingsdaten erfassen) befinden sich in den hochdimensionalen Daten. Es gibt eine vielfältige Hypothese, die als lokal verfestigt gilt. Ich denke, das folgende Beispiel für Schweizer Rollendaten ist leicht zu verstehen. Die Daten sind auf drei Dimensionen verteilt, aber die Daten sind ziemlich lokal voreingenommen, und Sie können sehen, dass die meisten Daten tatsächlich in zwei Dimensionen dargestellt werden können. Es gibt eine Lücke ohne Daten zwischen den Rollen. Daher sind die Daten, deren Abstand in drei Dimensionen nahe beieinander liegt, nicht immer ähnlich, und es ist wahrscheinlicher, dass ähnliche Daten gefunden werden, wenn der Abstand durch Bewegen in Richtung entlang der Phase berücksichtigt wird. Es ist also besser, es in zwei Dimensionen zu öffnen und den Abstand zu messen.
 [Schweizer Rolle als zweidimensionales mehrdimensionales in drei Dimensionen]
[Schweizer Rolle als zweidimensionales mehrdimensionales in drei Dimensionen]
 [Wenn Sie die Schweizer Rolle in zwei Dimensionen erweitern, sieht es so aus]
[Wenn Sie die Schweizer Rolle in zwei Dimensionen erweitern, sieht es so aus]
VAE kehrt von Swissroll zu MNISTs VAE zurück und erfasst diese Sorte und verschiebt sie von der 784-dimensionalen MNIST-Bilddatendimension in die latente Variable $ z \ sim N (0, 1) $ dimension. Siehe auch [7] zum Ausdruckslernen und zur Diversitätshypothese.
2. Implementierung mit Chainer
Ich werde die Verwendung einer angepassten Version basierend auf Chainer Official Example erläutern. Encoder und Decoder werden mit 3-Layer-MLP (Multi Layer Perceptron) modelliert.
Das von Chainer vor dem Code ausgegebene Berechnungsdiagramm ist unten dargestellt. Sie können sehen, dass der MLP-Teil der drei Schichten von Encoder und Decoder und die Verwendung von "Gauß", dh einer Zufallszahl, die einer Normalverteilung folgt, die latente Variable $ z $ erzeugen. Der Encoder drückt $ z $ aus, indem er die Parameter $ \ mu $ und $ \ sigma ^ 2 $ dieser Normalverteilung ausgibt.

# Reference: https://jmetzen.github.io/2015-11-27/vae.html
class Xavier(initializer.Initializer):
"""
Xavier initializaer
Reference:
* https://jmetzen.github.io/2015-11-27/vae.html
* https://stackoverflow.com/questions/33640581/how-to-do-xavier-initialization-on-tensorflow
"""
def __init__(self, fan_in, fan_out, constant=1, dtype=None):
self.fan_in = fan_in
self.fan_out = fan_out
self.high = constant*np.sqrt(6.0/(fan_in + fan_out))
self.low = -self.high
super(Xavier, self).__init__(dtype)
def __call__(self, array):
xp = cuda.get_array_module(array)
args = {'low': self.low, 'high': self.high, 'size': array.shape}
if xp is not np:
# Only CuPy supports dtype option
if self.dtype == np.float32 or self.dtype == np.float16:
# float16 is not supported in cuRAND
args['dtype'] = np.float32
array[...] = xp.random.uniform(**args)
# Original implementation: https://github.com/chainer/chainer/tree/master/examples/vae
class VAE(chainer.Chain):
"""Variational AutoEncoder"""
def __init__(self, n_in, n_latent, n_h, act_func=F.tanh):
super(VAE, self).__init__()
self.act_func = act_func
with self.init_scope():
# encoder
self.le1 = L.Linear(n_in, n_h, initialW=Xavier(n_in, n_h))
self.le2 = L.Linear(n_h, n_h, initialW=Xavier(n_h, n_h))
self.le3_mu = L.Linear(n_h, n_latent, initialW=Xavier(n_h, n_latent))
self.le3_ln_var = L.Linear(n_h, n_latent, initialW=Xavier(n_h, n_latent))
# decoder
self.ld1 = L.Linear(n_latent, n_h, initialW=Xavier(n_latent, n_h))
self.ld2 = L.Linear(n_h, n_h, initialW=Xavier(n_h, n_h))
self.ld3 = L.Linear(n_h, n_in,initialW=Xavier(n_h, n_in))
def __call__(self, x, sigmoid=True):
""" AutoEncoder """
return self.decode(self.encode(x)[0], sigmoid)
def encode(self, x):
if type(x) != chainer.variable.Variable:
x = chainer.Variable(x)
x.name = "x"
h1 = self.act_func(self.le1(x))
h1.name = "enc_h1"
h2 = self.act_func(self.le2(h1))
h2.name = "enc_h2"
mu = self.le3_mu(h2)
mu.name = "z_mu"
ln_var = self.le3_ln_var(h2) # ln_var = log(sigma**2)
ln_var.name = "z_ln_var"
return mu, ln_var
def decode(self, z, sigmoid=True):
h1 = self.act_func(self.ld1(z))
h1.name = "dec_h1"
h2 = self.act_func(self.ld2(h1))
h2.name = "dec_h2"
h3 = self.ld3(h2)
h3.name = "dec_h3"
if sigmoid:
return F.sigmoid(h3)
else:
return h3
def get_loss_func(self, C=1.0, k=1):
"""Get loss function of VAE.
The loss value is equal to ELBO (Evidence Lower Bound)
multiplied by -1.
Args:
C (int): Usually this is 1.0. Can be changed to control the
second term of ELBO bound, which works as regularization.
k (int): Number of Monte Carlo samples used in encoded vector.
"""
def lf(x):
mu, ln_var = self.encode(x)
batchsize = len(mu.data)
# reconstruction error
rec_loss = 0
for l in six.moves.range(k):
z = F.gaussian(mu, ln_var)
z.name = "z"
rec_loss += F.bernoulli_nll(x, self.decode(z, sigmoid=False)) / (k * batchsize)
self.rec_loss = rec_loss
self.rec_loss.name = "reconstruction error"
self.latent_loss = C * gaussian_kl_divergence(mu, ln_var) / batchsize
self.latent_loss.name = "latent loss"
self.loss = self.rec_loss + self.latent_loss
self.loss.name = "loss"
return self.loss
return lf
3. Theoretischer Überblick über VAE
Der Zweck des generierten Modells besteht darin, die Verteilung der Daten $ p (X) $ zu schätzen. In den Worten von PRML ist es wie folgt.
Der Ansatz der impliziten oder expliziten Modellierung der Verteilung von Eingaben sowie der Verteilung von Ausgaben wird als ** generatives Modell ** bezeichnet, da durch Eingabe aus dem Modell künstliche Daten im Eingaberaum generiert werden können. " PRML Band 1 S. 42)
Bei der Betrachtung von Bildern sind $ X $ normalerweise sehr hochdimensionale Daten. Da dieser Artikel auf MNIST abzielt, handelt es sich um 784-dimensionale Daten. Wie im vorherigen Abschnitt beschrieben, gibt es in dieser höheren Dimension nur sehr wenige Stellen, an denen Daten tatsächlich vorhanden sind. Daher haben wir sie gut erfasst und die latente Variable $ z des unteren Dimensionsfaktors (z. B. 10. Dimension). Erwägen Sie, es mit $ auszudrücken. Mit anderen Worten, wir versuchen, eine Entsprechung zwischen hochdimensionalen Daten $ X $ und niedrigdimensionalen Daten $ z $ herzustellen und sie gut zu verwenden. VAE trainiert diese latente Variable $ z $ als Normalverteilung und schätzt $ p (X) $. $ p (X) $ wird manchmal als Beweis bezeichnet.
Hier,
- $ p (\ cdot) $: Wahrscheinlichkeitsmodell
- $ z $: Latente Variable
- $ X $: Daten
Wird besorgt. Da diese Wahrscheinlichkeitsverteilung Parameter enthält, kann die wahrscheinlichste Methode für $ p (X) $ verwendet werden, um den Parameter für $ p (X) $ zu finden, der $ X $ am besten darstellt. In VAE wird ein neuronales Netzwerk für einige der Elemente verwendet, aus denen diese Wahrscheinlichkeitsverteilung besteht, und seine Parameter werden durch das Fehlerrückausbreitungsverfahren und das stochastische Gradientenabstiegsverfahren erhalten.
Das grafische Modell zeigt die Beziehung zwischen der latenten Variablen $ z $ und den Daten $ X $.

Das neuronale Netzwerk, das die latente Variable $ z $ mit den Daten $ X $ verknüpft, heißt Encoder. Wenn Sie über die Analogie der Bilddateikomprimierung wie das sogenannte JPEG nachdenken, können Sie sehen, warum es Encoder heißt.

Umgekehrt ist Decoder ein neuronales Netzwerk, das Daten $ X $ aus der latenten Variablen $ z $ wiederherstellt.

Aus dem Obigen kann die VAE, die aus Encoder, Decoder und zwei neuronalen Netzen besteht, wie folgt modelliert werden. $ \ phi $ ist der Encoder-Parameter und $ \ theta $ ist der Decoder-Parameter. Der Punkt ist, dass Encoder nicht direkt $ z $ generiert, sondern die normalverteilten Parameter $ \ mu, \ sigma $, denen $ z $ folgt, wie unten gezeigt.

Wir haben festgestellt, dass das Modell $ p (X) $, das wir schätzen möchten, ein Modell ist, das aus zwei neuronalen Netzen besteht, wie oben beschrieben. Der Rest ist das Verfahren, um die Parameter zu finden, die zu den Daten passen. In Anbetracht der folgenden Schritte können wir sehen, dass wir den Parameter finden sollten, der die Variationsuntergrenze $ L (X, z) $ maximiert (später beschrieben). Die untere Variationsgrenze wird manchmal als ELBO (Evidence Lower BOund) bezeichnet.
** Schritte zum Nachdenken über das Finden von Parametern **
- Finden Sie die neuronalen Netzwerkparameter $ \ theta, \ phi $, die die Wahrscheinlichkeit von $ p (X) $ mit der wahrscheinlichsten Methode maximieren.
- Ziel ist es, die Protokollwahrscheinlichkeit $ \ log p (X) $ zu maximieren, um die Verwendung zu vereinfachen.
- Da es schwierig ist, die Integration zu handhaben, indem $ \ log p (X) $ so wie sie ist maximiert wird, wird die untere Variationsgrenze $ L (X, z) $ maximiert und von unten nach unten verschoben, um sie zu unterdrücken Suchen Sie den Parameter, der den Grad maximiert.
Was ist die Untergrenze dieser Variation? Dies wird wie folgt berechnet.
 Informationen zur Jensen-Ungleichung finden Sie auch unter [hier](http://qiita.com/kenmatsu4/items/26d098a4048f84bf85fb).
Informationen zur Jensen-Ungleichung finden Sie auch unter [hier](http://qiita.com/kenmatsu4/items/26d098a4048f84bf85fb).
Aufgrund der Ungleichung stellt $ L (X, z) $ die Untergrenze von $ \ log p (X) $ dar, und es gibt eine Lücke, wie durch das "?" In der folgenden Abbildung dargestellt.

Protokollieren Sie die Wahrscheinlichkeit, dieses "?"

In der letzten Formel ist sie größer oder gleich 0, da die Divergenz der Calback Libra immer größer oder gleich 0 ist.

Daher ist die untere Variationsgrenze

ist geworden. Da der erste Term ein fester Wert und der zweite Term ein parameterabhängiger Punkt ist, ist das Ziel "Maximierung der unteren Variationsgrenze" die Calback Libra-Divergenz.
Diese Calback Libra Divergenz

Setzen Sie dies in die Gleichung für die Untergrenze der Variation ein.

Jetzt wissen wir, dass die untere Variationsgrenze durch zwei Terme ausgedrückt werden kann.

Der zweite Punkt ist
mu, ln_var = self.encode(x)
batchsize = len(mu.data)
# reconstruction error
rec_loss = 0
for l in six.moves.range(k):
z = F.gaussian(mu, ln_var)
z.name = "z"
rec_loss += F.bernoulli_nll(x, self.decode(z, sigmoid=False)) / (k * batchsize)
Angenommen, $ p_ {\ theta} (X | z) $ folgt einer multivariaten Bernoulli-Verteilung (aus [3] C.1 Bernoulli MLP als Decoder) [F.bernoulli_nll](https://docs.chainer.org/ Der Verlust wird mit en / stabile / Referenz / generiert / chainer.functions.bernoulli_nll.html # chainer.functions.bernoulli_nll) berechnet. Mit anderen Worten, unter der Annahme, dass jedes Pixel einen Wert zwischen 0 und 1 annimmt, wird angenommen, dass die Ausgabe von VAE und das Eingabebild eine Kreuzentropie aufweisen. Dieser Verlust wird als Rekonstruktionsfehler bezeichnet.

Erster Gegenstand
self.latent_loss = C * gaussian_kl_divergence(mu, ln_var) / batchsize
Der Kernteil von 'gaussian_kl_divergence' ist wie folgt.
var = exponential.exp(ln_var)
mean_square = mean * mean
loss = (mean_square + var - ln_var - 1) * 0.5
Es berechnet die Calback Libra-Divergenz, wenn es einer Normalverteilung folgt. (Siehe [3] ANHANG B)

(Informationen zur Ableitung der Kullback-Leibler-Divergenz bei Normalverteilung finden Sie im Kommentarartikel hier.)
Jetzt können Sie berechnen, was Sie maximieren möchten. Da das Lernen des neuronalen Netzwerks mit dem Wert der Minimierung des Verlusts durchgeführt wird, werden die Parameter $ \ theta und \ phi $ optimiert, indem die untere Grenze der Variation mit minus als Verlustfunktion multipliziert wird.
Reparameterization Trick
Das letzte Problem besteht darin, dass in der vorherigen Struktur eine Wahrscheinlichkeitsverteilung von $ z \ sim N (\ mu (X), \ sigma (X)) $ dazwischen liegt, sodass die Methode der Fehlerrückübertragung verwendet wird. Es ist nicht möglich, sich unten zu bewerben. Eine Technik namens Reparameterization Trick wird verwendet, um dies zu lösen. Anstatt sich direkt mit $ z \ sim N (\ mu (X), \ sigma (X)) $ zu befassen, erzeugen Sie Rauschen bei $ \ varepsilon \ sim N (0, I) $ und $ z = \ mu Durch Verbinden in Form von (X) + \ varepsilon * \ sigma (X) $ wird VAE wie in der folgenden Abbildung gezeigt konstruiert, wobei die Wahrscheinlichkeitsvariable vermieden und dem blauen Pfeil in umgekehrter Reihenfolge gefolgt wird und die Fehlerrückausbreitungsmethode angewendet wird. Es ist etwas zu tun.

In Bezug auf den Chainer-Code gilt Folgendes.
mu, ln_var = self.encode(x)
batchsize = len(mu.data)
# reconstruction error
rec_loss = 0
for l in six.moves.range(k):
z = F.gaussian(mu, ln_var)
Bonus
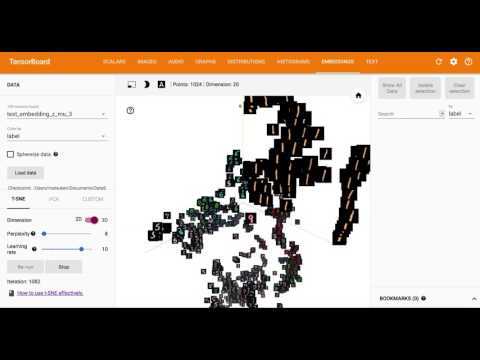
Mit Embedding, einer der Funktionen von Tensorboard von TensorFlow, wird die 20-dimensionale latente Variable $ z $ visualisiert, indem sie mit T-SNE in 3D und 2D reduziert wird.
Referenz
[1] Python-Code für diesen Artikel https://github.com/matsuken92/Qiita_Contents/tree/master/chainer-vae
[2] Tutorial on Variational Autoencoders https://arxiv.org/abs/1606.05908
[3] Auto-Encoding Variational Bayes(Diederik P Kingma, Max Welling) https://arxiv.org/abs/1312.6114
[4] Variante Bayes-Methode zur Verarbeitung natürlicher Sprache (Daichi Mochihashi) http://chasen.org/~daiti-m/paper/vb-nlp-tutorial.pdf
[5] Variational Auto Encoder (Sho Tatsuno), den selbst Katzen verstehen können https://www.slideshare.net/ssusere55c63/variational-autoencoder-64515581
[6] Deep Learning (Seiya Tokui) des generierten Modells https://www.slideshare.net/beam2d/learning-generator
[7] Expressionslernen mit dem IIBMP2016-Modell der tiefen Generation https://www.slideshare.net/pfi/iibmp2016-okanohara-deep-generative-models-for-representation-learning
[8] Variational AutoEncoder https://www.slideshare.net/KazukiNitta/variational-autoencoder-68705109
[9] Deep Learning Chapter 17 The Manifold Perspective on Representation Learning http://www.deeplearningbook.org/version-2015-10-03/contents/manifolds.html