Dieser Artikel ist der Artikel vom 21.12. Des WACUL Adventskalenders 2016.

Hallo, das Datenzeichen en Steam von WACUL ist @onhrs, dass die Arbeit der Datenanalyse.

Zuletzt habe ich an der Verarbeitung natürlicher Sprache und anderen Datenanalysen im Zusammenhang mit maschinellem Lernen gearbeitet.

Diesmal beschleunigen Dr. Hidetoshi Nishimori und Dr. Masayuki Ozeki [Quantencomputer beschleunigt künstliche Intelligenz](https://www.amazon.co.jp/ Quantencomputer beschleunigt künstliche Intelligenz - Nishimori-Hidetoshi / dp / 4822251896 / ref = sr_1_1? Dh = UTF8 & qid = 1489141470 & sr = 8-1 & keywords = Nishimori% E3% 80% 80 Quantum), also im Einklang mit dem Inhalt des Buches ** Künstliche Intelligenz x Quantencomputer ** Ich möchte über ... reden. (Wir wollten, dass Menschen, die Physik und Mathematik nicht verstehen, es verstehen.)

Ich habe auch versucht, mit Python einen Überblick zu geben, ohne Formeln zu verwenden. Auch wenn ich die Details nicht verstehe, habe ich versucht, sie sichtbar und verständlich zu machen.

Ich bin motiviert, andere Artikel als den Adventskalender zu veröffentlichen, daher wäre ich Ihnen dankbar, wenn Sie es möchten. (Lol)

Zielgruppe dieses Artikels

・ Diejenigen, die etwas über Quantencomputer und Quantenglühen wissen wollen ・ Diejenigen, die den aktuellen Status und das zukünftige Potenzial von Quantencomputern kennenlernen möchten ・ Diejenigen, die die Beziehung zwischen Quantencomputern und künstlicher Intelligenz kennen wollen ・ Diejenigen, die mit Python in die Datenwissenschaft einsteigen möchten

Erwartete Umgebung

Sprache: Python3 Sie benötigen NumPy, SciPy, Matplotlib usw., können aber Anaconda hinzufügen.

Herausgeber: Jupyter (Natürlich sind andere Herausgeber in Ordnung)

Als Schlüsselwort

Ich denke, es wird esoterische Wörter und unbekannte Begriffe geben. Hier finden Sie eine Zusammenfassung der wichtigen Wörter, Schlüsselwörter und ihrer kurzen Übersichten zur Vorbereitung und zur späteren Überprüfung. (Es ist in Ordnung, wenn es Wörter gibt, die Sie zu diesem Zeitpunkt nicht verstehen. Überspringen Sie sie in diesem Fall.)

Die Bestellung ist angemessen.
Es ist keine strenge Definition, sondern es gibt Orte, an denen wir lügen, weil wir Klarheit anstreben, aber bitte rekonstruieren Sie sie, nachdem Sie sie verstanden haben. (Lacht) Um ein richtiges Verständnis zu haben, ist es wichtig, ** statistische Mechanik ** und ** Quantenmechanik ** zu verstehen.

Maschinelles Lernen

Es ist schwer so einfach zu erklären wie diese Wörter, aber es geht darum, statistische Methoden zu verwenden, um die Muster zu finden, die aus ihnen erhalten werden können. Dies ist eine unverzichtbare Methode für die aktuelle Big-Data-Analyse.

Tiefes Lernen (oder tiefes Lernen)

Eine Methode zum maschinellen Lernen mit einer Methode, die das Gehirn imitiert (neuronales Netzwerk).

Dies ist sehr nützlich, wenn Sie über viele Daten verfügen, einschließlich der Bildbeurteilung.

Genau genommen muss es nicht unbedingt eine mehrschichtige Struktur sein, und Deep Learning muss nicht unbedingt eine neuronale Netzwerkstruktur sein.

Quantencomputer

Im Gegensatz zu dem herkömmlichen Computer, der mit Binärzahlen von '0' und '1' berechnet, wird '** Welle **' in der mikroskopischen (extrem expandierenden) Welt von Atomen und Molekülen erzeugt, die als Quantenmechanik bezeichnet wird. Ein Computer, der die Eigenschaften von verwendet.

Quantenglühen

Das Optimierungsproblem, bei dem die Berechnung aller Pfade sehr lange dauert, wird mit hoher Geschwindigkeit unter Verwendung des oben genannten Wellenphänomens der Quantenmechanik berechnet. Auch als Quantenbrennmethode bekannt.

Quantenbit

Während normale Bits nur '0' und '1' darstellen können, sind Quantenbits, wie oben erwähnt, Wellen, so dass sie überlagert werden können. Sie können die Mehrdeutigkeit von 1 und 0 ausdrücken. (Details können durch Verstehen der Quantenverschränkung verstanden werden.)

Quantenverschränkung

Es ist der Quantenzustand der obigen Überlagerung selbst. Da eine Substanz auch eine Welle in der Quantenwelt ist, wird sie überlagert, also ist es der Zustand selbst. (Vielleicht ist das das Verständnis.)

Um es schwierig auszudrücken: Wenn zwei Teilchen (Wellen) betrachtet werden, ist es die Korrelation, die sie voneinander erhalten. Wenn ein Zustand bestimmt wird, wird auch der andere Zustand bestimmt. Die Quantenteleportation nutzt dieses Phänomen.

Simuliertes Glühen

Aus dem Phänomen des "Backens" wird abgeleitet, dass die Kristallstruktur schön wird, wenn die Temperatur langsam gesenkt wird, während sich das Metall auf einer hohen Temperatur befindet, und diese Methode zur Minimierung der Kristallenergie wird durch eine numerische Berechnung ersetzt und ist optimal. Dies ist ein klassischer Weg, um das Konvertierungsproblem zu lösen.

Quantum-Gate-Methode

Ein Verfahren, bei dem Quantenbits zur Berechnung in einen Halbleiter eingebaut werden. Der herkömmliche Quantencomputer bezieht sich häufig auf dieses Verfahren, aber mit dem Aufkommen des Quantencomputers zum Quantenglühen wurde die Position umgekehrt.

Dieser Quantencomputer vom Typ Quantengatter lief nicht gut, da der Quantenzustand leicht kollabieren konnte.

Tunneleffekt

Im Quantenzustand kann eine Substanz als eine Welle betrachtet werden, die eine probabilistische Welle ist, die unter bestimmten Umständen Energiebarrieren eher "durchläuft" als überwindet.

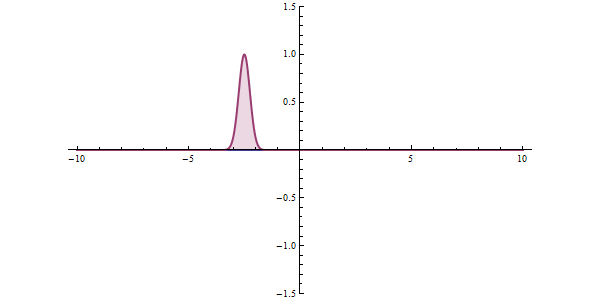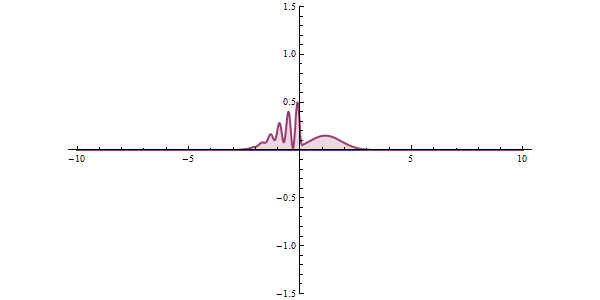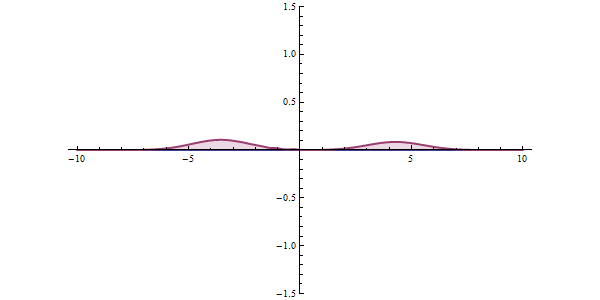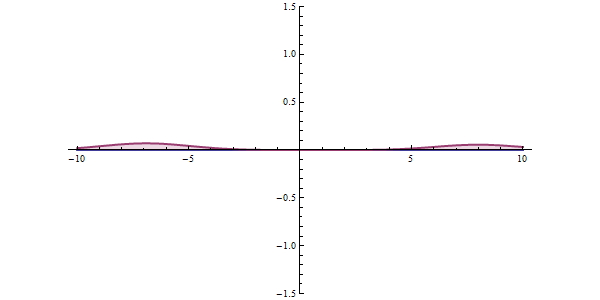
https://ja.wikipedia.org/wiki/%E3%83%88%E3%83%B3%E3%83%8D%E3%83%AB%E5%8A%B9%E6%9E%9C

rotieren

Es ist die kleinste Einheit eines Magneten. Das Elektron, das die kleinste Stromeinheit ist, hat die Eigenschaft der Rotation. Dies ist zu drehen. Ausgedrückt als (nach oben, unten) oder (nach rechts, gegen den Uhrzeigersinn)

~~ Es scheint, dass Leute, die sich auf Elementarteilchen spezialisiert haben, wirklich wütend werden (lacht) ~~ Gehen wir weiter, ohne uns darum zu kümmern

Steigendes Modell

Es ist ein Modell zur Realisierung des Quantenglühens, und es ist möglich, den Zustand, der den Energiezustand der obigen Spins minimiert, zur Lösung des Optimierungsproblems zu machen.

D-Wave

Ein Unternehmen, das die Theorie von Professor Nishimori, der sich für das Quantenglühen einsetzte und den weltweit ersten kommerziellen Quantencomputer herstellte, in die Praxis umsetzte.

Über das Problem des Handlungsreisenden, das selbst mit einem Supercomputer nicht gelöst werden kann

Reisender Verkäufer Bei der Betrachtung des Problems berücksichtigt ein Verkäufer die Route, die die Entfernung minimiert, wenn er durch mehrere Städte reist.

Zum Beispiel drei Städte (zB Tokio, Nagoya und Osaka) Tokio → Osaka → Nagoya → Tokio und Tokio → Nagoya → Osaka → Tokio, Es scheint dasselbe zu sein, in die entgegengesetzte Richtung zu gehen, also ist es 1 für 3 Städte.

Auszug aus [Quantum Computer 1] Plötzlich kommerzialisierte Traummaschine (3/6)

Verallgemeinern

\frac{(n-1)!}{2}Straße

ist. Wenn Sie es also in Python schreiben (ich glaube nicht, dass Sie es schreiben müssen)

#Patrouillenverkäufer Problem
import math

def travelingSales(n):
    return math.factorial(n-1)/2

Mit diesem, 8 Städte

travelingSales(8)
2520

In 15 Städten

travelingSales(15)
43589145600.0(45,3 Milliarden)

In 20 Städten

travelingSales(20)
6.0822550204416e+16

In 30 Städten

travelingSales(30)
4.420880996869851e+30

…

Es wird sein. Bis zu 20 Städte können mit einem Supercomputer in wenigen Sekunden gelöst werden, aber 30 Städte würden 14 Millionen Jahre dauern, was zu lang ist.

Das Obige ist der Umriss des Problems der reisenden Verkäufer.

Referenz: [Quantum Computer 1] Dream Machine plötzlich kommerzialisiert: ITpro

Was soll ich dann tun?

In der Praxis gibt es verschiedene Möglichkeiten, verschiedene Näherungen zu berechnen, um das obige Problem zu lösen. Ich werde mich jedoch auf das simulierte Tempern konzentrieren, das mit dem Quantenglühen zusammenhängt.

Zunächst einmal, wenn Sie die aktuelle Situation kurz zusammenfassen, scheint es, dass Menschen eine einfache kürzeste Route verstehen können, aber da sich der Computer die Mühe machen muss, die kürzeste Route zu berechnen, nachdem alle Kombinationen von Routen berücksichtigt wurden, Selbst wenn es ungefähr 30 Städte gab, war die Route selbst unzählig und konnte nicht gelöst werden.

Um ein konkretes Beispiel zu erläutern, werde ich anhand des offiziellen Dokuments von Scipy erläutern.

"Optimierungsprobleme sind Probleme, die numerische Lösungen für Mindestwerte und Gleichungen finden. Das Modul scipy.optimize minimiert Funktionen (skalar und mehrdimensional) und passt Kurven an. Und es bietet einen praktischen Algorithmus für die Wurzelsuche. (Aus Offizielles Dokument)

Zeichnen Sie das Optimierungsproblem mit optimize.fmin_bfgs mithilfe des BFGS-Algorithmus und berechnen Sie es tatsächlich.

Definieren wir die folgende Funktion und lösen das Optimierungsproblem.

f(x)=x^2+15sin(1.2x) \\ (-10\leqq x\leqq10)

from scipy import optimize

def minfunc(x):
    return x**2+ 15*np.sin(1.2*x)


x = np.arange(-10, 10, 0.1)
plt.plot(x, minfunc(x))

Sie können es leicht finden, indem Sie optimize.fmin_bfgs (Funktion, Anfangswert, disp = 0) festlegen.

#disp=0 gibt nur den Mindestwert an
optimize.fmin_bfgs(minfunc, 0,disp=0)

Der erhaltene Wert ist

array([-1.19776296])

Sicherlich wurde der visuell erkennbare Mindestwert erreicht.

Allerdings vorläufig im zweiten Argument von optimize.fmin_bfgs

#Anfangswert x=-Auf 5 setzen
optimize.fmin_bfgs(minfunc, -5, disp=0)
array([-5.94383045])

#Anfangswert x=Auf 3 setzen
optimize.fmin_bfgs(minfunc, 3, disp=0)
array([ 3.58552219])

#Anfangswert x=Auf 10 setzen
optimize.fmin_bfgs(minfunc, 10, disp=0)
array([ 8.20653212])

Dann wird es wie oben sein.

Aus dem Anfangswert kann nur der Wert von y erhalten werden, wenn der Differentialkoeffizient 0 ist (die Stelle, an der der Ball in der Delle gefangen ist, wenn der Ball von der angegebenen Stelle gerollt wird).

Bei der Annahme, dass die vertikale Richtung des Diagramms die Entfernung ist, die die Stadt patrouilliert, und die horizontale Achse die Anzahl der Muster, die die Stadt patrouillieren (obwohl dies etwas aggressiv erscheint), ist $ (-10 \ Nehmen Sie für alle leqq x \ leqq10) $ optimize.fmin_bfgs als Beispiel, probieren Sie verschiedene Anfangswerte aus, und der niedrigste Wert ist der Mindestwert (dh der Mindestwert der in der Stadt zurückgelegten Strecke). ist.

Wenn Sie gründlich danach suchen, wird es schließlich schwierig sein, es zu lösen, wenn es 30 Muster wie das Problem des reisenden Verkäufers erreicht.

Um die obigen Probleme zu lösen, gibt es eine Technik, die als simuliertes Tempern bezeichnet wird.

Beim simulierten Tempern wird eine Wahrscheinlichkeitsverteilung angegeben, die Verteilung wird zuerst groß gemacht und dann wird die Verteilung der Wahrscheinlichkeiten allmählich verengt (diese Arbeit ist der Teil, in dem die Temperatur des herkömmlichen "Backens" allmählich gesenkt wird. Selbst wenn es im obigen Beispiel noch gefangen ist (Differenzkoeffizient ist 0), beendet es die Berechnung an diesem Punkt nicht und sucht den endgültigen Mindestwert.

Selbst mit dieser Methode scheint es weniger Berechnung als Quetschen zu erfordern, aber im Falle eines komplizierten Problems wird es gezwungen sein, eine große Menge an Berechnungen durchzuführen, und eine große Menge an Energie wird benötigt, um der Falle zu entkommen. wird benötigt werden.

Beim Quantenglühen wird dies durch den ** Tunneleffekt ** gelöst, der ein Quantenphänomen ist.

Zusätzlich zur probabilistischen Suche nach simuliertem Tempern ist es durch Suchen mit Wellen im Quantenzustand möglich, einen Tunneleffekt aus der eingeschlossenen Position zu erzeugen und leicht zum Minimalwert zu gelangen.

Wie oben beschrieben, scheint es möglich zu sein, das Problem des Handlungsreisenden unter Verwendung des Quanteneffekts für das herkömmliche simulierte Tempern zu berechnen. (In "Quantencomputer beschleunigt künstliche Intelligenz" wurde geschrieben, dass es "100 Millionen Mal" sein würde.)

Der Tunneleffekt besteht darin, dass die Partikelwelle unter bestimmten Bedingungen wahrscheinlich herausquillt, sodass es unwahrscheinlich ist, dass der Tunnel so leicht auf die optimale Lösung fällt, aber der Grund dafür ist persönlich. Als Hausaufgabe möchte ich es zu einem späteren Zeitpunkt herausfinden.

Steigendes Modell, das tatsächlich Quantenglühen ermöglicht

Dann gibt es tatsächlich ein "Ising-Modell" als Modell, um die optimale Lösung unter der Situation zu lösen, die Quantenglühen ermöglicht.

In Bezug auf die Atomgröße erscheint die Eigenschaft des Spins, die die kleinste Einheit eines Magneten ist. Eigentlich ist es klein und unzusammenhängend, daher ist es normalerweise unsichtbar, aber in einem besonderen Zustand sind die Drehungen ausgerichtet und als Ergebnis werden die Eigenschaften als Magnet geboren. (* Das Studium des "Magnetismus" im Bereich der Magnete ist äußerst schwierig !!)

Diese Spin-Eigenschaft hat nur zwei Zustände, aufwärts und abwärts. (Für diejenigen, die wissen, kann der Energiezustand des quantisierten Zustands nur diskrete Werte annehmen.)

Das Zing-Modell ist ein Modell, das unter Verwendung dieser Eigenschaft von "Spin" berechnet, die sichtbar ist, wenn es klein ist. (Ich werde die Geschichte der Interaktion und die Formel selbst weglassen, um das steigende Modell zu berechnen, weil es schwierig ist.)

Ich weiß nicht, wovon Sie in der Erklärung sprechen, also werfen wir einen konkreten Blick darauf.

Um die Berechnung zu vereinfachen, werden wir die Dimensionen reduzieren und in zwei Dimensionen diskutieren. (Kurz gesagt, lassen Sie uns in der Welt der Animation ohne Tiefe diskutieren.)

Die ursprüngliche Geschichte lautet Ich werde das Ising-Modell auf einfache Weise erklären Und Monte-Carlo-Simulation des Ising-Modells mit Python Beziehen Sie sich darauf, da es implementiert ist (insbesondere wurde der frühere Code erklärt und verbessert).

Zum Animieren verwende ich artistAnimation von matplotlib, um mehrere Bilder in den Array-Ims aufzuzeichnen und sie tatsächlich mit ArtistAnimation auszuführen. http://qiita.com/yubais/items/c95ba9ff1b23dd33fde2

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pandas import Series, DataFrame
from numpy.random import randint, randn, rand
import math
import matplotlib.animation as animation


#Spielen Sie die Matplotlib-Animation auf Jupyter
%matplotlib nbagg

#Anzahl der Atome
Size = 50 

#J ist eine Konstante, die die Wechselwirkung zwischen Spins darstellt
J = 1

#Magnetfeld
H = 0

#Temperatur[K]
Temp = 0


#Kehrt sich der Spin um?
def spin_direction(field, x, y):
    energy = H

    '''
Periodische Randbedingung
(Weil das am Rand befindliche Atom keinen Kontakt mit den vier Atomen hat
Nur in diesem Fall bewegt es sich parallel.)
    '''
    for dx, dy in [(-1,0), (1,0), (0,-1), (0,1)]:

        if x + dx < 0: 
            dx += Size
        if y + dy < 0: 
            dy += Size
        if x + dx >= Size: 
            dx -= Size
        if y + dy >= Size: 
            dy -= Size

        #Energieberechnung
        energy += J * field.iloc[x + dx, y + dy]

    if Temp == 0:
        #np.Vorzeichen ist 1 für positiv und 1 für negativ für jedes Element-Wenn es 1, 0, 0 ist, wird 0 zurückgegeben.
        p = (np.sign(energy) + 1) * 0.5
    else:
        #Wahrscheinlichkeit der Spinumkehr mit Temperatur und Energie (T.=(Außer wenn es 0 ist)
        p = 1/(1+np.exp(-2*(1/Temp)*energy))
        #Ob der oben berechnete Spin eine höhere Inversionswahrscheinlichkeit aufweist als eine Gleitkomma-Zufallszahl zwischen 0 und 1.
    if rand() <= p:
        spin = 1
    else:
        spin = -1
    return spin





#Ich weiß nicht viel über Gibbs Sampling.
def run_gibbs_sampling(field, iternum=5):
    for _ in range(iternum):
        lattice = DataFrame([(y,x) for x in range(Size) for y in range(Size)])

        #Reindex ordnet die Position des Atoms entsprechend neu zu
        lattice = lattice.reindex(np.random.permutation(lattice.index))

        #lattice.Werte ist die Position jedes Gitterpunkts. Zum Beispiel[0,0]Wenn ja, 0. vertikal und 0. horizontal
        for x, y in lattice.values:

            #Berechnen Sie, ob der Spin umgekehrt ist
            field.iloc[x, y] = spin_direction(field, x, y)




fig = plt.figure()
field = DataFrame(randint(2,size=(Size,Size))*2-1)

temps = [0.,.5,1.,1.5,2.,2.5,5.0,10.0][::-1]

ax1=fig.add_subplot(1,2,1)
ax2=fig.add_subplot(1,3,3)
ax2.axis(xmin=-1,xmax=10.5)
ax2.set_xlabel("time")
ax2.set_ylabel("T[K]")


ims = []


for i in range(1,9):

    Temp = temps[i-1]
    run_gibbs_sampling(field)
    im1 = ax1.imshow(field.values, vmin=-1, vmax=1,cmap=plt.cm.gray_r, interpolation='nearest')
    x=np.arange(1, 9, 1)
    im2,=ax2.plot(x[0:i], temps[0:i],marker="o",markersize=12,color = "red")

    ims.append([im1,im2])

ani = animation.ArtistAnimation(fig, ims, interval = 1000)

#Ziel speichern (falls erforderlich)
#ani.save("ising.gif")

plt.show()

Wenn sich die Temperatur 0 K nähert (die absolute Temperatur beträgt –273,15 $ {} ^ \ circ \ mathrm {C} $ ist 0 K), werden die disjunkten Spinzustände stabil (d. H. Niedrigenergiezustände). Dann können Sie sehen, wie die Aufwärts- und Abwärtsrichtung lokalisiert sind.

Der wahre stabile Zustand ist, dass alles auf oder ab ist, aber es ist zufällig nebeneinander, wenn die Temperatur sinkt, weil es wahrscheinlich disjunkt war (genauer gesagt, disjunkt durch die Schwingung von Atomen aufgrund der Temperatur). Einige der Drehungen sind lokalisiert, da sie die Eigenschaft haben, in dieselbe Richtung zu zeigen.

Die Spinwechselwirkung wird durch die Größe von J bestimmt.

Wenn ein Magnetfeld angelegt wird (vorausgesetzt, der Magnet wird näher gebracht), muss es nur ausgeführt werden (H = 0,5 im obigen Code).

Hier weisen sie aufgrund der Kraft des Magnetfelds alle in der Nähe von T = 2K in die gleiche Richtung.

Nach wie vor können Sie sehen, dass Dinge, die zufällig lokalisiert wurden, alle in die gleiche Richtung ausgerichtet sind, bevor sie mithilfe des Magnetfelds lokalisiert werden.

Bisher haben wir das zweidimensionale Inging-Modell erklärt. (Es war lang.)

Nach diesem Modell ist das Quantenglühen eine Anwendung des Optimierungsproblems, das tatsächlich den stabilen Zustand des Spins einer Substanz anwendet.

Der eigentliche Quantencomputer ist eine dreidimensionale Erweiterung des obigen aufsteigenden Modells. Ausgehend von diesem Modell hat der Spin auf mysteriöse Weise nur zwei Zustände: Auf und Ab.

Durch Anlegen eines Magnetfelds von der Seite an eine Substanz, die eine dreidimensionale Erweiterung des Zing-Modells darstellt, wird ein Überlagerungszustand nach oben und unten (Quantenverschränkungszustand) von Spins erzeugt.

Wenn dieses transversale Magnetfeld auf die gleiche Weise allmählich verringert wird, wie die Temperatur zuvor gesenkt wurde, wird die Spinwechselwirkung zwischen Atomen größer, und der Spin-Energiezustand, wenn das transversale Magnetfeld 0 ist, ist der zu lösende Minimalwert. Nehmen.

Wie oben beschrieben, kann durch Optimieren des Überlagerungszustands (Quantenverschränkungszustand) von Spins mit einem tatsächlichen Material, selbst beim simulierten Tempern, das Optimierungsproblem, das einen großen Rechenaufwand erfordert, durch das Quantenphänomen (insbesondere Tunnel) gelöst werden. Es wird durch den Effekt realisiert).

Ich habe versucht, selbst eine Figur zu zeichnen, war aber erschöpft. Einzelheiten finden Sie auf der Website, die ich zuvor vorgestellt habe. (Kann später bearbeitet und aktualisiert werden) http://itpro.nikkeibp.co.jp/article/COLUMN/20140514/556566/

Bezieht es sich auf maschinelles Lernen und tiefes Lernen?

Es wird erwartet, dass es in den Bereichen maschinelles Lernen und tiefes Lernen sowie KI (oder maschinelles Lernen) angewendet wird, die sich in den letzten Jahren rasant entwickelt haben, wie z. B. Probleme bei der Optimierung des Anlageportfolios, Bildauthentifizierung, medizinische Versorgung, Recht und Archäologie. Auf dem Gebiet scheint dieser Quantencomputer in der Lage zu sein, sie zu beschleunigen. Darüber hinaus versucht Google mit dem Aufkommen von D-Wave ernsthaft, einen Quantencomputer mit dieser Methode zu realisieren, und man kann sagen, dass die Anwendungsfelder durch Quantenglühen sehr unterschiedlich sind. (Weitere Einzelheiten zu diesem Bereich finden Sie in Professor Nishimoris "Quantencomputer beschleunigt künstliche Intelligenz".)

Am Ende

Als Nachrüstung arbeite ich derzeit als Datenwissenschaftler, um Big Data (hauptsächlich Webdaten) mithilfe von KI (maschinelles Lernen oder Statistik) zu analysieren. Ich bin jedoch eine Graduiertenschule. Also habe ich ein Element namens Spin-Transistor untersucht, das einen Quanten-Gate-Quantencomputer realisiert.

KI- und Quantencomputer, von denen damals angenommen wurde, dass sie nichts miteinander zu tun haben, haben in den letzten Jahren begonnen, sich zu engagieren, und es war überraschend, dass Quantencomputer eine wichtige Rolle bei der Verwirklichung einer echten KI spielen. (Universitätsforschung wurde nicht verschwendet.)

Auch die Quantenmechanik und das Zing-Modell sind immer noch sehr tiefgreifend, deshalb habe ich beschlossen, diese Gelegenheit zu nutzen, um mehr zu studieren. (Jetzt war ich zu dieser Zeit frustriert [Randaus statistische Physik](https://www.amazon.co.jp/%E7%B5%B1%E8%A8%88%E7%89%A9%E7%90%86] % E5% AD% A6-% E4% B8% 8A-% E3% 82% A8% E3% 83% AA% E3% 83% BB% E3% 83% A9% E3% 83% B3% E3% 83% 80 Sie sollten% E3% 82% A6 / dp / 4000057200 lesen können) (lacht)

Spin, Quantenmechanik und statistische Mechanik sind Disziplinen, die die Mikrowelt diskutieren und nicht in ein oder zwei Tagen verstanden werden können. Wenn Sie diese Gelegenheit nutzen, um verschiedene Dinge zu studieren, sollten Sie in der Lage sein, den Spaß und die Aufmerksamkeit zu verstehen. (Ursprünglich war dieses Buch die Nummer eins in der Kategorie Physik von Amazon.)

* Als Einzelausgabe

Ein genauer Überblick darüber, wie der Tunneleffekt das Erreichen der optimalen Lösung erleichtert als beim herkömmlichen simulierten Glühen.

・ Über Gibbs Sampling

Ich möchte das oben genannte verstehen und wieder einen Artikel schreiben (lacht)

Wenn Sie offensichtliche Fehler oder Fragen haben, teilen Sie uns dies bitte mit. Ich werde es reparieren.

Ich las "Quantencomputer beschleunigt künstliche Intelligenz" und versuchte, es in Python ohne mathematische Formeln zu skizzieren.