[PYTHON] Beschleunigung der numerischen Berechnung mit NumPy / SciPy: Anwendung 1
Ziel
Es wurde für Anfänger von Python und NumPy geschrieben. Es kann besonders nützlich sein für diejenigen, die eine numerische Berechnung physikalischer Systeme anstreben, die "Ich kann C-Sprache verwenden, habe aber kürzlich Python gestartet" oder "Ich verstehe nicht, wie man wie Python schreibt" entspricht. Vielleicht.
Außerdem kann es aufgrund meines mangelnden Studiums zu falschen Beschreibungen kommen. Bitte verzeihen Sie mir.
Zusammenfassung
Der Inhalt ist eine Fortsetzung von Beschleunigen der numerischen Berechnung mit NumPy: Basics Ich werde die grundlegende numerische Berechnung ohne Verwendung implementieren. SciPy wird ab diesem Zeitpunkt der Gruppe beitreten. Ich habe die detaillierte Implementierung der NumPy / SciPy-Funktionen unten nicht viel kommentiert. Wenn Sie also Fragen haben, zögern Sie bitte nicht, uns zu kontaktieren. Bitte lesen Sie die Referenz. Unnötig zu sagen: ** Es ist sehr wichtig, die Räder nicht neu zu erfinden. **
Differential
Die Grundgleichungen der Physik gehen mit einer Differenzierung einher. Da es sich bei der Differenzierung um eine lineare Abbildung handelt, kann sie durch eine Matrixgleichung beschrieben werden. Nehmen wir beispielsweise an, wir berechnen die doppelte Differenzierung einer Funktion. Wir werden dies anhand der Vorwärtsdifferenz und der Rückwärtsdifferenz ausdrücken. Masu:
\frac{d^2}{dx^2}\psi(x) = \frac{\psi(x + \Delta x) - 2\psi(x) + \psi(x - \Delta x)}{\Delta x^2} + {\cal O}(\Delta x^2)
Wenn Sie $ \ psi (x) $ um $ \ Delta x $ verteilen
\psi(x)\rightarrow \{\psi(x_0), \psi(x_1), ..., \psi(x_{n-1}), \psi(x_n)\} = \{\psi_0, \psi_1, ..., \psi_{n-1}, \psi_n\}\hspace{1cm}x_i = -L/2 + i\Delta x
Differenzierungen können in Matrixform geschrieben werden:
\frac{d^2}{dx^2}\psi(x) = \frac{1}{\Delta x^2}
\begin{pmatrix}
\psi_{-1} -2\psi_0 + \psi_1\\
\psi_0 -2\psi_1 + \psi_2\\
\vdots\\
\psi_{n-2} -2\psi_{n-1} + \psi_n\\
\psi_{n-1} -2\psi_n + \psi_{n+1}
\end{pmatrix}
\simeq \frac{1}{\Delta x^2}
\begin{pmatrix}
-2&1&0&\cdots&0\\
1&-2 &1&&0\\
0 & 1&-2&& \vdots\\
\vdots&&&\ddots&1\\
0& \cdots& 0 &1& -2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix}
=K\psi
Es hat etwas Unangenehmes, aber es ist in Ordnung, wenn $ \ Delta x $ klein ist. Jetzt ist es hier, wenn Sie eine Warteschlange erstellen können.
Implementierung
Ich werde es in Python implementieren. Ich werde einige anfängliche Funktionen vorbereiten und sie unterscheiden:
>>> import numpy as np
>>> def f(x):
... return np.exp(-x**2)
...
>>> L, N = 7, 100
>>> x = np.linspace(-L/2, L/2, N)
>>> psi = f(x)
>>> psi
array([ 4.78511739e-06, 7.81043424e-06, 1.26216247e-05,
2.01935578e-05, 3.19865883e-05, 5.01626530e-05,
7.78844169e-05, 1.19723153e-04, 1.82206228e-04,
...,
2.74540100e-04, 1.82206228e-04, 1.19723153e-04,
7.78844169e-05, 5.01626530e-05, 3.19865883e-05,
2.01935578e-05, 1.26216247e-05, 7.81043424e-06,
4.78511739e-06])
Bereiten Sie dann eine Differenzierungsmatrix vor. Dazu müssen Sie die Werte in der unteren diagonalen Komponente speichern. ** Kombinieren Sie also die Scheibe von ndarray mit np.vstack **:
>>> K = np.eye(N, N)
>>> K
array([[ 1., 0., 0., ..., 0., 0., 0.],
[ 0., 1., 0., ..., 0., 0., 0.],
[ 0., 0., 1., ..., 0., 0., 0.],
...,
[ 0., 0., 0., ..., 1., 0., 0.],
[ 0., 0., 0., ..., 0., 1., 0.],
[ 0., 0., 0., ..., 0., 0., 1.]])
>>> K_sub = np.vstack((K[1:], np.array([0] * N)))
>>> K_sub
array([[ 0., 1., 0., ..., 0., 0., 0.],
[ 0., 0., 1., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 0., 0., 0.],
...,
[ 0., 0., 0., ..., 0., 1., 0.],
[ 0., 0., 0., ..., 0., 0., 1.],
[ 0., 0., 0., ..., 0., 0., 0.]])
>>> K = -2 * K + K_sub + K_sub.T
>>> K
array([[-2., 1., 0., ..., 0., 0., 0.],
[ 1., -2., 1., ..., 0., 0., 0.],
[ 0., 1., -2., ..., 0., 0., 0.],
...,
[ 0., 0., 0., ..., -2., 1., 0.],
[ 0., 0., 0., ..., 1., -2., 1.],
[ 0., 0., 0., ..., 0., 1., -2.]])
Wenn Sie das Produkt damit nehmen, ist die Differenzierung zweiter Ordnung abgeschlossen:
dx = L/N
psi_2dot = dx**-2 * np.dot(K, psi)
Ich könnte es schreiben, ohne die for-Schleife zu verwenden. Währenddessen ** gibt es tatsächlich eine Funktion zum Berechnen des Gradienten namens gradient **:
psi_dot_np = np.gradient(psi, dx)
psi_2dot_np = np.gradient(psi_dot_np, dx)
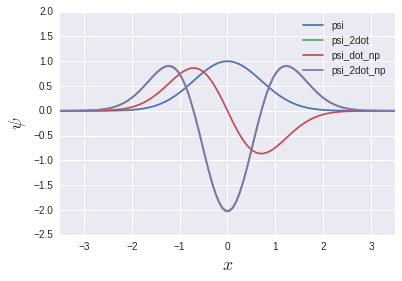
psi_2dot und psi_2dot_np überschneiden sich fast vollständig. Sie mögen denken, dass die vorherige Matrixgeschichte keinen Sinn ergibt, aber wir werden das Tageslicht in einem späteren Kapitel über Eigenwertgleichungen wieder sehen. Wird sein.
Integration
Ein bekannter Algorithmus für die numerische Integration wäre die Simpson-Integration:
\int_a^b dx\; f(x) = \sum_{i=0}^{n-1}\frac{h}{6}\left[f(x_i) + 4f\left(x_i + \frac{h}{2}\right) + f(x_i + h)\right]\hspace{1cm}x_i = a + ih
Der Beweis ist mit Lagrange Completion einfach, aber ich werde ihn hier weglassen.
Implementierung
Die Implementierung würde folgendermaßen aussehen:
>>> simp_arr = f(x) + 4 * f(x + dx / 2) + f(x + dx)
>>> dx / 6 * np.sum(simp_arr)
1.75472827313
Ich mag die Einfachheit, den Ausdruck so wie er ist in den Code einzufügen. ** Die Simpson-Integration wird jedoch in Abhängigkeit von SciPy bereitgestellt: **
>>> from scipy.integrate import simps
>>> simps(psi, x)
1.7724525416390826
Die Berechnungsergebnisse unterscheiden sich geringfügig, da SciPy die Simpson-Regel verwendet, die genauer ist. Wenn Sie keinen bestimmten Grund haben, ist es besser, diese zu verwenden, als sie selbst zu erstellen. ** Darüber hinaus Differenzierung Es gibt auch eine Funktion, die die vorherige Funktion übergibt und integriert: **
>>> from scipy.integrate import quad
>>> quad(f, -np.inf, np.inf)
(1.7724538509055159, 1.4202636780944923e-08)
Sie kann durch Angabe einer Funktion und eines Integrationsintervalls berechnet werden. Der Rückgabewert ist Tupel, die erste Komponente ist das Integrationsergebnis und die zweite Komponente ist der absolute Fehler. "Quad" verwendet die Technik in der Fortran-Bibliothek QUADPACK. Es scheint [^ 1]. ** Eigentlich ist dieses Kind sehr gut. ** Hier sind einige Dinge, für die ich dankbar bin:
- ** Scheint eine adaptive Integration zu verwenden, die die extreme Breite nach Bedarf ändert **
Bei der Simpson-Integration ist die Breite der Differenz räumlich einheitlich, bei der adaptiven Integration jedoch "wenn feine Unterschiede erforderlich sind (wenn sich die Funktion heftig bewegt), fein sind und wenn nicht viel Bedarf besteht (die Bewegung der Funktion ist). Es scheint so, als würde es so etwas wie "Verbreiten der Breite (an einem ruhigen Ort)" bewirken. Die Berechnung wird schneller sein, während die Genauigkeit des Fehlers erhalten bleibt. Sie sind möglicherweise nicht so dankbar für eine gewöhnliche eindimensionale Integration. Wenn es jedoch um die Doppel- und Dreifachintegration geht, ist sie unvergleichlich schneller als die Simpson-Integration [^ 2]. Sie ist viel schneller als die von mir selbst in C / C ++ erstellte Simpson-Integration.
- ** Sie können dem Integrationsintervall
np.infgeben **
Bei einer kompakten Funktion wie dieser hängt die Entfernung des Integrationsintervalls von der erforderlichen Berechnungsgenauigkeit ab. Bei Verwendung von "np.inf" ist die Berechnungsgenauigkeit jedoch ein Argument für "Quad", ohne sich um den Grenzwert sorgen zu müssen. Es wäre schön, es in "Epsabs, Epsrel" usw. zu werfen.
- ** Einfach zu verwenden **
Wahrscheinlich eine viel einfachere Oberfläche als das direkte Berühren von QUADPACK [^ 3].
Eigenwertgleichung
Lassen Sie uns nun ein wenig über die Quantenmechanik sprechen. Lassen Sie uns die Eigenfunktionen und Energieeigenwerte eines eindimensionalen harmonischen Oszillatorsystems finden. Hamiltonian
H = \frac{\hat{p}^2}{2} + \frac{\hat{q}^2}{2} = -\frac12\frac{d^2}{dq^2} + \frac{q^2}{2}
Dies ist ein Kind. Es verwendet ein Einheitensystem von $ \ hbar = \ omega = m = 1 $. Schrödinger-Gleichung für diesen Hamilton-Operator
H\psi_\ell(q) = E_\ell\psi_\ell(q)
$ \ Ell $ ist nicht der Index der Differenz, sondern der Index des Eigenwerts / der Eigenfunktion. Zunächst wird der potenzielle Term in ein Matrixformat differenziert:
\frac{q^2}{2}\psi(q) \rightarrow \frac12
\begin{pmatrix}
q_0^2&0&0&\cdots&0\\
0&q_1^2 &0&\cdots&0\\
0 & 0&q_2^2&& \vdots\\
\vdots&&&\ddots&0\\
0& \cdots& 0 &0& q_n^2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix}=\frac12
\begin{pmatrix}
(-L/2)^2&0&0&\cdots&0\\
0&(-L/2 + \Delta q)^2 &0&&0\\
0 & 0&(-L/2 + 2\Delta q)^2&& \vdots\\
\vdots&&&\ddots&0\\
0& \cdots& 0 &0& (L/2)^2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix} = V\psi
Ich weiß nicht, ob Hajikko genau $ L / 2 $ sein wird, aber das ist richtig. Ich erinnere mich an das, was ich im Kapitel Differenzierung getan habe, die Schrödinger-Gleichung
H\psi = (K + V)\psi = \frac12
\begin{pmatrix}
\frac{2}{\Delta q^2} + (-L/2)^2&\frac{-1}{\Delta q^2}&0&\cdots&0\\
\frac{-1}{\Delta q^2}&\frac{2}{\Delta q^2} + (-L/2 + \Delta q)^2 &\frac{-1}{\Delta q^2}&&0\\
0 & \frac{-1}{\Delta q^2}&\frac{2}{\Delta q^2} + (-L/2 + 2\Delta q)^2&& \vdots\\
\vdots&&&\ddots&\frac{-1}{\Delta q^2}\\
0& \cdots& 0 &\frac{-1}{\Delta q^2}& \frac{2}{\Delta q^2} + (L/2)^2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix} = E_\ell\psi
Es sieht aus wie.
Implementierung
Jetzt ist es Codierung.
#Systemeinstellungen
>>> L, N = 10, 200
>>> x, dx = np.linspace(-L/2, L/2, N), L / N
#Übungsbegriff K.
>>> K = np.eye(N, N)
>>> K_sub = np.vstack((K[1:], np.array([0] * N)))
>>> K = dx**-2 * (2 * K - K_sub - K_sub.T)
#Mögliche Laufzeit
>>> V = np.diag(np.linspace(-L/2, L/2, N)**2)
#Hermeet-Matrix-Eigenwertgleichung
#w ist ein eindeutiger Wert,v ist der Eigenvektor
>>> H = (K + V) / 2
>>> w, v = np.linalg.eigh(H)
Die Definition von "dx" ist subtil, aber keine Sorge:
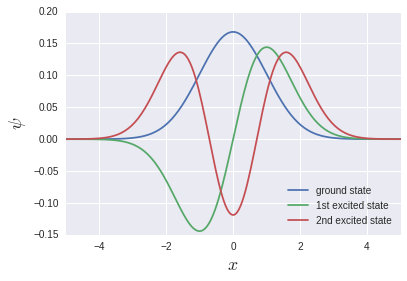
Es werden einzigartige Funktionen ausgegeben, die häufig in Lehrbüchern verwendet werden.
np.linalg.eigh ist ein Löser von Eigenwertgleichungen für Elmeet, der Eigenwerte und Eigenfunktionen zurückgibt. Diesmal handelt es sich um eine dreifach diagonale Matrix, also np.linalg.eig_banded für Bandmatrizen Ich denke jedoch, dass die Geschwindigkeit in np.linalg.eigh [^ 4] eher höher ist. Der Speicherverbrauch ist in np.linalg.eig_banded wahrscheinlich geringer.
** Hierbei ist zu beachten, dass der Grundzustand, der erste angeregte Zustand, der zweite angeregte Zustand ... in "v [0], v [1], v [2] ..." gespeichert sind Stattdessen bedeutet dies "vT [0], vT [1], vT [2] ...". ** Dies bedeutet, dass die Speicherung von Array-Daten im Speicher für das C-System Row-Major und für Fortran Fortran ist. Wahrscheinlich aufgrund der Diskrepanz zwischen Spalte und Haupt. Wenn np.linalg.eigh ein Wrapper für LAPACK ist, kann dies in gewissem Sinne ein natürliches Verhalten sein.
Berechnen wir die Differenz zwischen den Eigenwerten und untersuchen die Anregungsenergie. Geben wir etwa 20 von der Basis aus:
>>> np.diff(w)[:20]
[ 1.00470938 1.00439356 1.00407832 1.00376982 1.00351013 1.00351647
1.00464172 1.00938694 1.02300462 1.05279364 1.10422331 1.17688369
1.26494763 1.36132769 1.46086643 1.56082387 1.66005567 1.75820017
1.85521207 1.95115074]
Die Anregungsenergie des harmonischen Oszillatorsystems beträgt unabhängig vom Pegel $ \ hbar \ omega $, daher ist sie in diesem Einheitensystem 1. Sie wird im Niedrigenergiebereich ziemlich gut reproduziert, im Hochenergiebereich jedoch ziemlich verdächtig. Versuchen wir, den 15. angeregten Zustand auszugeben:
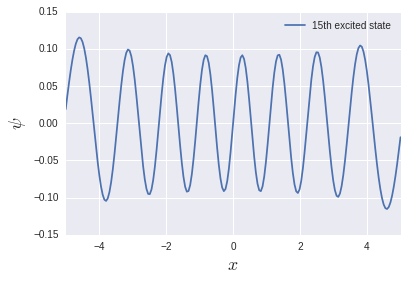
Es gibt 15 Knoten, aber die Funktion ist am Rand nicht kompakt. Deshalb war die Raumgröße von $ L = 10 $ nicht ausreichend. Ich möchte genau berechnen, welcher Anregungszustand vorliegt. Es ist notwendig, die Größe des Raums und die Anzahl der Unterteilungen zu ändern.
Die analytische Berechnung der Eigenwerte und Eigenfunktionen eines harmonischen Oszillators ist eine ziemlich mühsame Aufgabe, aber es ist sehr einfach, sie in numerische Berechnungen einzubeziehen [^ 5].
Differentialgleichung
Eindimensionale Diffusionsgleichung
\frac{\partial}{\partial t}f(x, t) = \frac{\partial^2}{\partial x^2}f(x, t)
Dieses Kind kann unter den Anfangsbedingungen [^ 6] eine analytische Lösung durch die Fourier-Transformation von $ x $ finden, aber diesmal lösen wir sie natürlich numerisch Geben Sie die Bedingungen in Gauß an und beginnen Sie mit der üblichen räumlichen Differenzierung:
f(x, 0) = \exp(-x^2)\\
f_k \equiv f(k\Delta x, t), \hspace{0.7cm} \Delta x = L/N
Dann werden auch die Differentialgleichungen unterschieden:
\frac{d}{dt}f_0 = \frac{f_1 - 2f_0}{\Delta x^2}\\
\frac{d}{dt}f_1 = \frac{f_2 - 2f_1 + f_0}{\Delta x^2}
...\\
\frac{d}{dt}f_k = \frac{f_{k+1} - 2f_k + f_{k-1}}{\Delta x^2}\\
...\\
\frac{d}{dt}f_{n-1} = \frac{f_{n} - 2f_{n-1} + f_{n-2}}{\Delta x^2}\\
\frac{d}{dt}f_n = \frac{-2f_n + f_{n-1}}{\Delta x^2}
SciPy nimmt eine Liste von Differenzierungen einer Funktion "[f0, f1, ..., fn-1, fn]" als Argument und entwickelt sie im Laufe der Zeit um $ \ Delta t $ ("ndarray"). Es gibt einen Löser der Differentialgleichung namens ** odeint, der die Differentialgleichung lösen kann, indem er eine Funktion übergibt, die zurückgibt. **
Implementierung
Lassen Sie uns zuerst diese Funktion erstellen:
from scipy.integrate import odeint
def equation(f, t=0, N, L):
dx = L / N
gamma = dx**-2
i = np.arange(1, N, 1)
# f0
arr = np.array(gamma * (f[1] - 2 * f[0]))
# f1 to fN-1
arr = np.append(arr, gamma * (f[i+1] - 2 * f[i] + f[i-1]))
# fN
arr = np.append(arr, gamma * (-2 * f[N] + f[N-1]))
return arr
Sie werden irgendwie wissen, was Sie tun. In dieser Funktion schreiben wir das differenzierte $ f $ in Form eines Arrays wie f [n]. F istf [0] Es besteht aus $ N + 1 $ Elementen vonbis f [N]. Außerdem ist das erste Argument eine differenzierte Liste von Funktionen f und das zweite Argument ist die Zeit t. Ist die Spezifikation von odeint. Stellen Sie sicher, dass Sie diese Reihenfolge verwenden. Die Anfangszeit ist natürlich $ t = 0 $, daher wird der Standardwert festgelegt. ** # f1 bis fN-1 Übrigens, ohne "[gamma * (f [j + 1] -2 * f [j] + f [j-1]) für j in i]" zu schreiben, liste einfach "i" auf, was "ndarray" ist. Ich finde es nüchtern, dass es in Ordnung ist, es einfach in den Index von zu setzen. **
** --Zusatz (03.12.2016) - ** Immerhin ist es nur eine Differenzierung zweiter Ordnung
from scipy.integrate import odeint
def equation(f, t=0, N, L):
dx = L / N
arr = np.gradient(np.gradient(f, dx), dx)
return arr
Es ist gut. Gradient unterscheidet sich von diff und es ist wunderbar, dass sich die Größe der Liste nach der Verarbeitung nicht ändert.
** - Ergänzung hier - **
Die anfängliche Funktion ist übrigens
def f(x):
return np.exp(-x**2)
Es war.
Es gibt auch einige Variablen, die an "odeint" selbst übergeben werden müssen. Eine ist die oben definierte "Gleichung (f, t0, ...)" und die zweite ist das "ndarray", das die Anfangsfunktion unterscheidet. "(Es scheint, dass iterabel gut ist), die dritte ist eine Liste der zu berechnenden Zeit" t ". Da" Gleichung "andere Variablen als" f "und" t0 "hat, ist ihre Existenz" Ich muss odeint sagen, also speichere ich diese Informationen in args`. Codiert unter Berücksichtigung dieser:
# initial parameter(optional)
N, L = 200, 40
# coordinate
q = np.linspace(-L/2, L/2, N)
# initial value for each fk
fk_0 = f(q)
# time
t_max, t_div = 10, 5
t = np.linspace(0, t_max, t_div)
trajectories = odeint(equation, fk_0, t, args=(N, L))
Die Zeitlösung für t [i] wird in Trajektorien [i] gespeichert. Zeichnen wir nun Folgendes:

Ich konnte sehen, wie sich Gauß ausbreitet. Dieses Mal habe ich mich mit der Diffusionsgleichung befasst, daher war der Code etwas verwirrend mit den beiden Variablen $ (x, t) $. Die gewöhnliche Differentialgleichung mit einer Variablen Ich denke, es wäre einfacher. Beim Plotten verwenden wir für Schleifen, aber ... das ist in Ordnung. Es ist wichtig, dass wir bei der numerischen Berechnung keine Schleifen (einschließlich Listeneinschlüsse) verwenden.
abschließend
Es ist lange her, also werde ich den Rest in einem anderen Artikel zusammenfassen. Wenn jemand sagt "Es gibt einen besseren Weg!", Wäre ich dankbar, wenn Sie einen Kommentar abgeben könnten.
Sie können sehen, dass NumPy und SciPy ein breiteres Verteidigungsspektrum haben als ich erwartet hatte. Als ich nach einer Referenz suchte, die "Vielleicht ..." dachte, hatte ich bereits etwas, das ich selbst implementiert hatte [^ 7] Dies ist häufig der Fall. ** Dies gilt nicht nur für NumPy / SciPy, sondern auch für die Standard-Python-Module. ** Bitte beachten Sie die Python-Referenz. Ich bin sicher, es gibt ein Paket.
** Nachtrag (25.11.2016): Fortsetzung unten ** Beschleunigung der numerischen Berechnung mit NumPy / SciPy: Anwendung 2
[^ 1]: Ich habe nicht überprüft, ob es QUADPACK umschließt. Das Handbuch sagt "... mit einer Technik aus der Fortran-Bibliothek QUADPACK".
[^ 2]: Ich denke, Monte Carlo ist schneller als 7 oder 8 Schichten.
[^ 3]: Ich habe es nicht benutzt, also weiß ich es ehrlich gesagt nicht.
[^ 4]: Es scheint, dass der Bandmatrixlöser schließlich das, was im Band übergeben wird, in ein Matrixformat erweitert und dann berechnet. In diesem Fall habe ich das Gefühl, dass sich der Speicherverbrauch doch nicht ändert ... ist.
[^ 5]: Natürlich sollte der Physiker mit der numerischen Berechnung nicht zufrieden sein. Da die numerische Berechnung allein keine qualitative Diskussion ermöglichen kann, wird auch ein System, das nicht genau gelöst werden kann, angenähert und analytisch. Es ist sehr sinnvoll, eine Lösung zu finden.
[^ 6]: Wir lösen Differentialgleichungen häufig durch Laplace-Transformation in elektronischen Schaltkreisen, aber es ist im Wesentlichen dasselbe. Wenn wir eine Anfangsfunktion vorbereiten, die nicht analytisch integriert werden kann, werden wir sie am Ende numerisch lösen. In diesem Sinne ist Gauß eine kompakte, analytisch integrierbare, sehr gute Funktion.
[^ 7]: Und oft viel besser als das, was ich implementiert habe.
Recommended Posts