[PYTHON] Entwurfsmuster #Strategie

Ich habe Designmuster geübt, um Code zu schreiben, der sich des Designs bewusst war. Andere Entwurfsmuster werden häufig veröffentlicht.

Vorwort

Einführung in in Java-Sprache erlernte Entwurfsmuster wurde von Java in Python geändert. (Python ist 3.4.2)
Der Code befindet sich auf Github (einige funktionieren immer noch nicht)

Das Hauptziel ist zu verstehen, wann, was und wie Entwurfsmuster verwendet werden. (Ich bin neu in Java oder einer statisch typisierten Sprache und habe keine lange Geschichte mit Python. Ich denke, es gibt einige Dinge, die Pythonista nicht ähneln. Wenn Sie Vorschläge haben, bringen Sie mir dies bitte bei.)

Diesmal das Muster Strategie zum Verhalten.

Was ist Strategie?

Der Teil, der den Algorithmus implementiert, kann in einem kurzen Blick ausgetauscht werden. Ein Muster, das es einfach macht, Algorithmen zu wechseln und dasselbe Problem unterschiedlich zu lösen.

Dies liegt daran, dass das Strategiemuster den Algorithmus-Teil bewusst von den anderen Teilen trennt. Und nur die Schnittstelle (API) mit dem Algorithmus wird angegeben. Dann wird der Algorithmus durch Delegierung aus dem Programm verwendet. Sie können problemlos zwischen Algorithmen wechseln, indem Sie die losen Delegierungsbindungen verwenden.

Das Strategiemuster kann verwendet werden, wenn viele Verhaltensweisen als mehrere bedingte Anweisungen angezeigt werden.

Überblick

Das hier erstellte Beispielprogramm dient zum Ausführen von "Janken" auf einem Computer. Ich dachte an zwei Methoden als die "Strategie" von Janken. Einer ist "Wenn Sie gewinnen, werden Sie beim nächsten Mal den gleichen Zug machen" (WinningStrategy) und der andere ist "Probabilistisch den nächsten Zug aus dem vorherigen Zug berechnen" (ProbStrategy).

Gesamtklassendiagramm

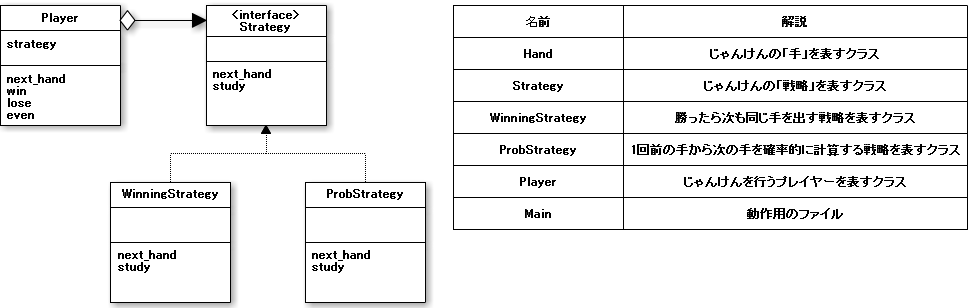
`hand.py`


class Hand():
    HANDVALUE_ROCK = 0
    HANDVALUE_SCISSORS = 1
    HANDVALUE_PAPER = 2
    NAMES = ['Schmiere', 'Choki', 'Par']
    HANDS = [HANDVALUE_ROCK,
             HANDVALUE_SCISSORS,
             HANDVALUE_PAPER]

    def __init__(self, handvalue):
        self.__handvalue = handvalue

    def get_hand(self, handvalue):
        return self.HANDS[self.__handvalue]

    def is_stronger_than(self, h):
        return self.__fight(h) == 1

    def is_weaker_than(self, h):
        return self.__fight(h) == -1

    def __fight(self, h):
        if self.__handvalue == h.__handvalue:
            return 0
        elif (self.__handvalue + 1) % 3 == h.__handvalue:
            return 1
        else:
            return -1

    def to_string(self):
        return self.NAMES[self.__handvalue]

Die Hand-Klasse ist eine Klasse, die die "Hand" von Janken darstellt. Innerhalb der Klasse ist goo 0, choki 1 und par 2. Speichern Sie dies als Handwertfeld.

Es können nur drei Instanzen der Hand-Klasse erstellt werden. Zunächst werden drei Instanzen erstellt und in den Array-HANDS gespeichert.

Sie können eine Instanz mit der Klassenmethode get_hand abrufen. Wenn Sie einen Handwert als Argument angeben, ist die Instanz der Rückgabewert.

is_stronger_than und is_weaker_than vergleichen die Handstärke. Verwenden Sie diese Option, wenn Sie zwei Hände haben, hand1 und hand2.

Innerhalb dieser Klasse ist es eine Methode namens Kampf, die tatsächlich die Stärke der Hand bestimmt. Der Wert der Hand wird verwendet, um die Stärke zu beurteilen. Der hier verwendete (Selbst .__ Handwert + 1)% 3 == h .__ Handwert ist der Wert der Hand des Selbst plus 1 als Wert der Hand von h (wenn Selbst gut ist, ist h Choki, Selbst Wenn choki ist, h par ist und wenn self par ist, h goo ist), dann ist self stärker als h. Der Grund für die Verwendung des Operators% für den Rest von 3 ist, dass wenn 1 zu Par (2) hinzugefügt wird, es zu goo (0) wird.

`strategy.py`


from abc import ABCMeta, abstractmethod


class Strategy(metaclass=ABCMeta):

    @abstractmethod
    def next_hand():
        pass

    @abstractmethod
    def study(win):
        pass

Die Strategie-Oberfläche ist eine Sammlung abstrakter Methoden für Jankens "Strategie".

next_hand ist eine Methode, um "den nächsten Zug zu machen". Wenn diese Methode aufgerufen wird, entscheidet die Klasse, die die Strategie-Schnittstelle implementiert, über den "nächsten Schritt".

Lernen ist eine Methode, um zu lernen, "ob Sie mit der Hand gewonnen haben, die Sie gerade ausgestreckt haben oder nicht". Wenn der vorherige Aufruf der next_hand-Methode gewinnt, rufen Sie ihn als study (True) auf. Wenn Sie verlieren, nennen Sie es als Studie (Falsch). Infolgedessen ändert die Klasse, die die Strategie-Schnittstelle implementiert, ihren internen Status und verwendet sie als Material, um den Rückgabewert der next_hand-Methode ab dem nächsten Mal zu bestimmen.

`winning_strategy.py`


import random
from hand import Hand
from strategy import Strategy


class WinningStrategy(Strategy):

    __won = False
    __prev_hand = 0

    def __init__(self, seed):
        self.__rand = seed

    def next_hand(self):
        if not(self.__won):
            self.__prev_hand = Hand(self.__rand).get_hand(random.randint(0, 3))
        return self.__prev_hand

    def study(self, win):
        self.__won = win

Die WinningStrategy-Klasse ist eine der Klassen, die die Strategy-Schnittstelle implementiert. Das Implementieren der Strategie-Schnittstelle bedeutet das Implementieren von zwei Methoden, next_hand und study.

Wenn Sie in dieser Klasse das vorherige Spiel gewinnen, werden Sie beim nächsten Mal dieselbe Strategie verfolgen (Goo für Goo, Par für Par). Wenn Sie das vorherige Spiel verlieren, wird der nächste Zug anhand von Zufallszahlen entschieden.

Das Rand-Feld enthält die Zufallszahlen, die diese Klasse verwendet, wenn sie benötigt wird.

Das gewonnene Feld enthält das Ergebnis des vorherigen Spiels. Wenn Sie gewinnen, ist es wahr, wenn Sie verlieren, ist es falsch.

Das Feld prev_hand enthält die Hand, die Sie im vorherigen Spiel ausgegeben haben.

`prob_strategy.py`


import random
from hand import Hand
from strategy import Strategy


class ProbStrategy(Strategy):

    __prev_hand_value = 0
    __current_hand_value = 0
    __history = [[1, 1, 1], [1, 1, 1], [1, 1, 1]]

    def __init__(self, seed):
        self.__rand = seed

    def next_hand(self):
        bet = random.randint(0, self.__get_sum(self.__current_hand_value))
        hand_value = 0
        if bet < self.__history[self.__current_hand_value][0]:
            hand_value = 0
        elif bet < self.__history[self.__current_hand_value][0] + \
                self.__history[self.__current_hand_value][1]:
            hand_value = 1
        else:
            hand_value = 2

        self.__prev_hand_value = self.__current_hand_value
        self.__current_hand_value = hand_value

        return Hand(hand_value).get_hand(hand_value)

    def __get_sum(self, hv):
        total = 0
        for i in range(0, 3):
            total += self.__history[hv][i]
        return total

    def study(self, win):
        if win:
            self.__history[self.__prev_hand_value][self.__current_hand_value] \
                += 1
        else:
            self.__history[self.__prev_hand_value][(self.__current_hand_value + 1) % 3] \
                += 1
            self.__history[self.__prev_hand_value][(self.__current_hand_value + 2) % 3] \
                += 1

Die ProbStrategy-Klasse ist eine weitere konkrete "Strategie". Der nächste Zug wird immer durch eine Zufallszahl entschieden, aber die Historie der vergangenen Gewinne und Verluste wird verwendet, um die Wahrscheinlichkeit jedes Zuges zu ändern.

Das Verlaufsfeld ist eine Tabelle zur Wahrscheinlichkeitsberechnung, die vergangene Gewinne und Verluste widerspiegelt. history ist ein zweidimensionales Array von Ganzzahlen, und die Indizes jeder Dimension haben die folgenden Bedeutungen.

Geschichte [Letzte Hand] [Diesmal] Je höher der Wert dieser Formel ist, desto höher ist die Gewinnrate in der Vergangenheit.

Wenn Sie im Detail schreiben. Verlauf [0] [0] Goo, die Anzahl der vergangenen Siege, wenn Sie es mit Goo löschen Geschichte [0] [1] Goo, Choki und die Anzahl der vergangenen Siege beim Löschen Geschichte [0] [2] Anzahl der vergangenen Siege bei Goo, Par und mir

Angenommen, Sie haben beim letzten Mal eine Gänsehaut herausgebracht. Zu diesem Zeitpunkt wird das, was ich als nächstes geben werde, mit Wahrscheinlichkeit aus den obigen Werten von "histroy [0] [0], history [0] [1], hisstroy [0] [2]" berechnet. Kurz gesagt, addieren Sie die Werte dieser drei Ausdrücke (Methode get_sum), berechnen Sie die Zahl aus 0 und entscheiden Sie dann den nächsten Zug basierend darauf (Methode next_hand).

Zum Beispiel Der Wert der Historie [0] [0] ist 3 Der Wert der Geschichte [0] [1] beträgt 5 Der Wert der Geschichte [0] [2] ist 7 Im Falle von. Zu diesem Zeitpunkt wird das Verhältnis von Goo, Choki und Par auf 3: 5: 7 eingestellt und der nächste Zug wird entschieden. Erhalten Sie einen zufälligen Wert zwischen 0 und weniger als 15 (15 ist ein Wert von 3 + 5 + 7), Goo wenn 0 oder mehr und weniger als 3 Choki wenn 3 oder mehr und weniger als 8 Par wenn 8 oder mehr und weniger als 15 Wird besorgt.

Die Untersuchungsmethode aktualisiert den Inhalt des Verlaufsfelds basierend auf dem Ergebnis der von der next_hand-Methode zurückgegebenen Hand.

`player.py`


class Player():

    __wincount = 0
    __losecount = 0
    __gamecount = 0

    def __init__(self, name, strategy):
        self.__name = name
        self.__strategy = strategy

    def next_hand(self):
        return self.__strategy.next_hand()

    def win(self):
        self.__strategy.study(True)
        self.__wincount += 1
        self.__gamecount += 1

    def lose(self):
        self.__strategy.study(False)
        self.__losecount += 1
        self.__gamecount += 1

    def even(self):
        self.__gamecount += 1

    def to_stirng(self):
        return '[{0}: {1} games {2} win {3} lose]'.format(self.__name,
                                                          self.__gamecount,
                                                          self.__wincount,
                                                          self.__losecount)

Die Spielerklasse ist eine Klasse, die die Person darstellt, die den Müll spielt. Die Player-Klasse erhält einen "Namen" und eine "Strategie" zum Erstellen einer Instanz. Die next_hand-Methode dient dazu, den nächsten Zug zu erhalten, aber es ist Ihre "Strategie", die tatsächlich den nächsten Zug bestimmt. Der Rückgabewert der next_hand-Methode der Strategie ist der Rückgabewert der next_hand-Methode des Spielers. Die next_hand-Methode "delegiert", was sie für die Strategie tun soll.

Die Spielerklasse ruft die Lernmethode durch das Startegy-Feld auf, um die Ergebnisse von Gewinnen (Gewinnen), Verlieren (Verlieren) und Zeichnen (Geraden) im nächsten Spiel zu verwenden. Verwenden Sie die Untersuchungsmethode, um den internen Status der Strategie zu ändern. wincount, losecount und geamecount zeichnen die Anzahl der Gewinne eines Spielers auf.

`main.py`


import random
import sys
from winning_strategy import WinningStrategy
from prob_strategy import ProbStrategy
from player import Player
from hand import Hand


def main():
    try:
        if int(sys.argv[1]) >= 3:
            seed1 = random.randint(0, 2)
        else:
            seed1 = int(sys.argv[1])

        if int(sys.argv[2]) >= 3:
            seed2 = random.randint(0, 2)
        else:
            seed2 = int(sys.argv[2])

        player1 = Player('Taro', WinningStrategy(seed1))
        player2 = Player('Hana', ProbStrategy(seed2))
        for i in range(0, 10):  # 10000
            next_hand1 = Hand(player1.next_hand())
            next_hand2 = Hand(player2.next_hand())
            if next_hand1.is_stronger_than(next_hand2):
                print('Winner : {0}'.format(player1.to_stirng()))
                player1.win()
                player2.lose()
            elif next_hand2.is_stronger_than(next_hand1):
                print('Winner : {0}'.format(player2.to_stirng()))
                player1.lose()
                player2.win()
            else:
                print('Even ...')
                player1.even()
                player2.even()

        print('Total result:')
        print(player1.to_stirng())
        print(player2.to_stirng())

    except IndexError:
        print('Check args size, does not work')
        print('usage: python main random_seed1 random_seed2')
        print('Example: python main.py 314 15')

if __name__ == "__main__":
    main()

Ausführungsergebnis

python main.py 21  3
Winner : [Hana: 0 games 0 win 0 lose]
Even ...
Winner : [Hana: 2 games 1 win 0 lose]
Winner : [Taro: 3 games 0 win 2 lose]
Even ...
Winner : [Taro: 5 games 1 win 2 lose]
Even ...
Winner : [Hana: 7 games 2 win 2 lose]
Winner : [Taro: 8 games 2 win 3 lose]
Winner : [Hana: 9 games 3 win 3 lose]
Total result:
[Taro: 10 games 3 win 4 lose]
[Hana: 10 games 4 win 3 lose]

Zusammenfassung

Das Strategiemuster trennt den Teil des Algorithmus bewusst von den anderen Teilen. Da eine lose Verbindung namens Delegation verwendet wird, ist es einfach, Algorithmen zu wechseln, wenn Sie den Schnittstellenteil nicht ändern.

[PYTHON] Entwurfsmuster #Strategie

Vorwort

Was ist Strategie?

Überblick

Gesamtklassendiagramm

hand.py

strategy.py

winning_strategy.py

prob_strategy.py

player.py

main.py