[PYTHON] Warum wird Kreuzentropie für die Zielfunktion des Klassifizierungsproblems verwendet?

Was ist ein Klassifizierungsproblem?

Das Klassifizierungsproblem klassifiziert Daten in mehrere Kategorien und ist eine der typischen Methoden des maschinellen Lernens.

Nehmen Sie als Beispiel eine Einkaufsseite. Sagen Sie anhand der Kaufinformationen eines Benutzers voraus, ob ein Benutzer ein neues Produkt kaufen wird oder nicht. Die Klassifizierung in zwei Kategorien (Klassen) wird als binäre Klassifizierung bezeichnet.

Klassifizierungsvorhersagen mit mehr als zwei Klassen werden als Klassifizierung mehrerer Klassen bezeichnet. Die Beurteilung von Objekten in Bildern (Bilderkennung) ist auch eines der Klassifizierungsprobleme mehrerer Klassen. Es ist auch ein Klassifizierungsproblem zu beurteilen, dass es sich um eine Katze handelt, basierend auf dem Bild der Katze.

Gekreuzte Entropie

Zwei Wahrscheinlichkeitsverteilungen

P(x):Richtige Datenverteilung\\
Q(x):Vorausschauende Modellverteilung

Im Gegensatz dazu wird die Kreuzentropie unten definiert.

L = - \sum_{x} P(x) \log{Q(x)}

Je ähnlicher die beiden Wahrscheinlichkeitsverteilungen sind, desto kleiner ist die Kreuzentropie. Unter Verwendung der Eigenschaften dieser Funktion wird sie häufig als objektive Funktion beim maschinellen Lernen (insbesondere bei Klassifizierungsproblemen) verwendet.

In diesem Artikel werden wir mathematisch untersuchen, warum Kreuzentropie häufig für objektive Funktionen verwendet wird.

Das Folgende war hilfreich für eine detaillierte Erklärung der Kreuzentropie. http://cookie-box.hatenablog.com/entry/2017/05/07/121607

Binäre Verteilung (Bernouy-Verteilung)

Nehmen Sie als Beispiel für die Klassifizierung das Klassifizierungsproblem, die einfachste Wahrscheinlichkeitsverteilung.

P(x_1) = p \;\;\; P(x_2) = 1 - p \\
Q(x_1) = q \;\;\; Q(x_2) = 1 - q \\

In der Box befinden sich zwei farbige Kugeln, rot und weiß, und die Wahrscheinlichkeit, rot zu zeichnen, ist

P(rot) = p

Die Wahrscheinlichkeit, weiß zu zeichnen

P(Weiß) = 1 - p

Es ist leicht zu verstehen, wenn Sie darüber nachdenken. Wenn Sie insgesamt 10 Bälle haben, 2 rote und 8 weiße

P(rot) = 0.2 \quad P(Weiß) = 0.8

darüber.

Zu diesem Zeitpunkt ist die Zielfunktion

\begin{align}
L &= - \sum_{x} P(x) \log{Q(x)} \\
  &= - p \log{q} - (1-p) \log{(1-q)}
\end{align}

Kann erweitert werden.

Betrachten Sie das folgende einfache neuronale Netzwerk. Stellen Sie sich ein Szenario vor, in dem Sie endlich die Wahrscheinlichkeitsverteilung $ q $ finden möchten. Um das vorherige Beispiel zu nennen, ich kenne den Inhalt der Box überhaupt nicht, aber ich werde einige Eingabedaten verwenden, um eine Wahrscheinlichkeitsverteilung zu erstellen, die eine rote Kugel als Modell zeichnet und das Ergebnis vorhersagt.

y = \sum_{i} x_i w_i \\
\\
q(y) = \frac{1}{1+e^{-y}} :Sigmaid-Funktion

Hier wird $ x_i $ eingegeben, $ w_i $ wird gewichtet, $ y $ ist ein Zwischenwert und $ q $ wird ausgegeben. Die typischste Sigmoidfunktion wird als Aktivierungsfunktion verwendet.

Neuronales Netzwerktraining

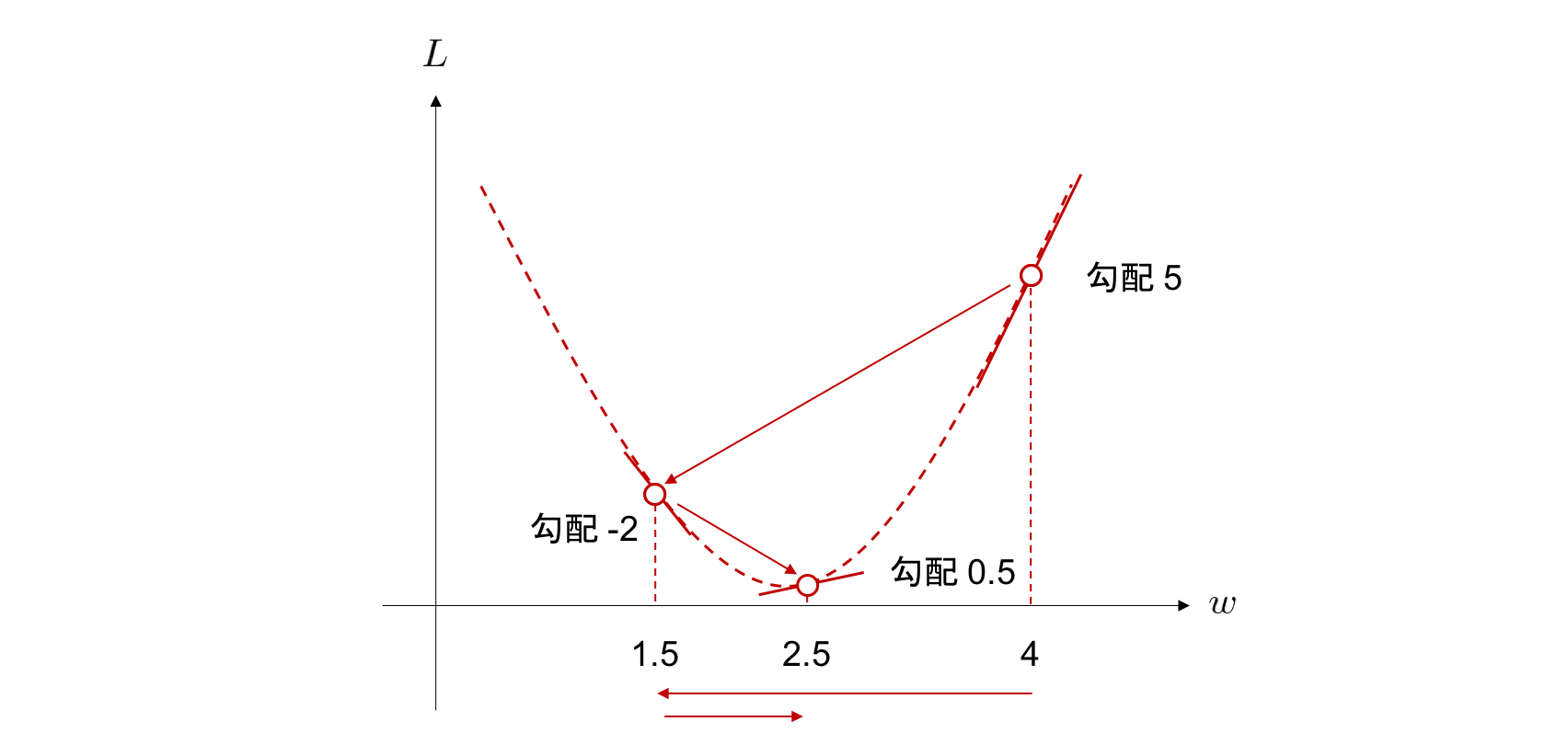
Trainieren Sie Ihr neuronales Netzwerk, indem Sie die Werte der Parameter ermitteln, die den Wert der Zielfunktion minimieren. Es verwendet einen der Optimierungsalgorithmen, ** Gradientenabstieg **.

w \leftarrow w - \eta \frac{\partial L}{\partial w}

Das Gradientenabstiegsverfahren ist ein Verfahren zum wiederholten Berechnen von ** Lernrate × Gradient der Zielfunktion **, um das Gewicht zu finden, das den Minimalwert der Zielfunktion annimmt.

Das folgende Chainer-Tutorial ist für eine detaillierte Erläuterung dieses Bereichs sehr einfach zu verstehen. https://tutorials.chainer.org/ja/13_Basics_of_Neural_Networks.html

Lassen Sie uns die Zielfunktion sofort unterscheiden.

\frac{\partial L }{\partial w_i} = \frac{\partial y}{\partial w_i} \frac{\partial q }{\partial y}\frac{\partial L }{\partial q}

Die erste Unterscheidung ist

\frac{\partial y}{\partial w_i} = \frac{\partial}{\partial w_i} \sum_i x_i w_i = x_i

Die zweite Unterscheidung ist

\begin{align}
\frac{\partial q }{\partial y} &= \frac{\partial}{\partial y} \frac{1}{1+e^{-y}} \\
&= \frac{\partial u}{\partial y}\frac{\partial}{\partial u} \frac{1}{u} \\
&= -e^{-y} (-u^{-2}) \\
&= \frac{e^{-y}}{1+e^{-y}}\frac{1}{1+e^{-y}} \\
&= \bigl( \frac{1+e^{-y}}{1+e^{-y}} - \frac{1}{1+e^{-y}} \bigr) \frac{1}{1+e^{-y}} \\
&= \bigl( 1-q(y) \bigr) q(y)
\end{align}

Die dritte Unterscheidung ist

\begin{align}
\frac{\partial L}{\partial q} &= \frac{\partial}{\partial q} \{ - p \log{q} - (1-p) \log{(1-q)} \} \\
&= - \frac{p}{q} + \frac{1-p}{1-q}

\end{align}

Weil es berechnet werden kann

\frac{\partial L }{\partial w_i} = x_i (1-q) q \bigl( - \frac{p}{q} + \frac{1-p}{1-q} \bigr) = x_i (q-p)

Mit anderen Worten

p = q

Wann ist, nimmt die Zielfunktion den Minimalwert an. Mit anderen Worten bedeutet dies, dass die Verteilung der korrekten Daten und die Verteilung des Vorhersagemodells genau gleich sind.

Nun, ich sage nur das Offensichtliche. Es gibt tatsächlich 8 Rot- und 2 Weißweine in der Schachtel Es sagt voraus, dass Rot 80% und Weiß 20% beträgt.

Auf Klassifizierungsprobleme anwenden

Lassen Sie uns nun die Variation als Klassifizierungsproblem etwas weiter erhöhen. Beispielsweise können in einem Klassifizierungsproblem Kategorien durch 0, 1 dargestellt werden.

Apfel: [1, 0, 0]
Gorira: [0, 1, 0]
Rappa: [0, 0, 1]

Wenn es etwas allgemeiner ist

Die richtige Antwort für die Klasse, zu der x gehört, lautet

t=[t_1, t_2 …t_K]^T

Im Vektor angegeben. Angenommen, dieser Vektor ist so, dass nur einer von $ t_k ; (k = 1,2,…, K) $ 1 und die anderen 0 sind. Dies wird als 1-Hot-Vektor bezeichnet.

Nachdem wir das Klassifizierungsproblem auf diese Weise definieren können, sieht die Zielfunktion folgendermaßen aus:

L = - \sum_x P(x) \log{ Q(x) } = - \log{ Q(x) }

$ Q (x) $ repräsentiert die Wahrscheinlichkeit, dass die Trainingsdaten mit den Lehrerdaten übereinstimmen. Lassen Sie es uns planen.

Bei der Gradientenabstiegsmethode wird das Gewicht $ w_i $, das die Zielfunktion minimiert, durch wiederholtes Berechnen der ** Lernrate × Gradient der Zielfunktion ** erhalten. Wenn die ** Lernrate ** extrem hoch ist oder wenn der ** Zielfunktionsgradient ** groß ist, scheint die Lerneffizienz gut zu sein. Es reduziert auch die Anzahl der Berechnungsschritte.

Es ist ersichtlich, dass für $ 0 <Q (x) <1 $ die Zielfunktion $ L $ nahe $ Q (x) = 0 $ stark abnimmt. Wenn die Lehrerdaten und das Lernergebnis zu unterschiedlich sind, kann daraus interpretiert werden, dass der Rückgang pro Schritt groß ist. Wenn Sie im Klassifizierungsproblem die Kreuzentropie als Zielfunktion auswählen, ist die Berechnungseffizienz gut.

Es ist leicht zu vergessen, ob Sie tatsächlich eine Bibliothek wie Chainer oder Pytorch verwenden. Es ist auch gut, auf die Grundtheorie zurückzublicken, um sie nicht zu vergessen. Ich habe viel gelernt.

Referenz https://mathwords.net/kousaentropy https://water2litter.net/rum/post/ai_loss_function/ http://yaju3d.hatenablog.jp/entry/2018/11/30/225841 https://avinton.com/academy/classification-regression/