Implementieren Sie die Erweiterung in Python

Überblick

In diesem Artikel werden wir den endlichen Körper und den erweiterten Körper kurz erklären und den Galois-Körper $ \ GF (2 ^ 4) \ $ in Python implementieren. Darüber hinaus implementieren wir die ElGamal-Verschlüsselung auf $ \ GF (2 ^ 4) \ $.

Über endlichen Körper

Die folgende Menge von primären $ \ p \ $ -Elementen ist der endliche Körper $ \ \ mathbb {F} _p \ $.

\mathbb{F}_p = \{ 0, 1, \cdots, p-1\}.

Addition und Multiplikation werden in dieser Menge beispielsweise definiert, wenn $ \ p = 5 \ $

2 + 3 = 0, \ \ 1 + 3 = 4,\ \  3 + 4 = 2,\\
2 \times 3 = 1,\ \  1 \times 3 = 3,\ \  3 \times 4 = 2.

Beachten Sie, dass für $ a, b \ in \ mathbb {F} _p \ $ die folgende Berechnung durchgeführt wird.

a + b \pmod{p},\\
a \times b \pmod{p}.

Der Punkt ist, dass die ursprüngliche Zahl eine Primzahl ist. Um es im Detail zu erklären, klingelt der Rest $ \ mathbb {Z} / p \ mathbb {Z} \ $ und $ \ \ mathbb {Z} / n \ mathbb { Lassen Sie sie in Z} \ $ erscheinen. $ P \ $ ist jedoch eine Primzahl und $ n \ $ ist eine nicht primäre zusammengesetzte Zahl. Der Überschussring ist ein schwieriger Name, aber er sieht so aus:

\mathbb{Z}/p\mathbb{Z} = \{ 0, 1, \cdots, p-1\},\\
\mathbb{Z}/n\mathbb{Z} = \{ 0, 1, \cdots, n-1\}.

Addition und Multiplikation sind auch in diesen definiert. Schreiben wir also eine "Multiplikationstabelle" für $ p = 5, n = 6 \ $.

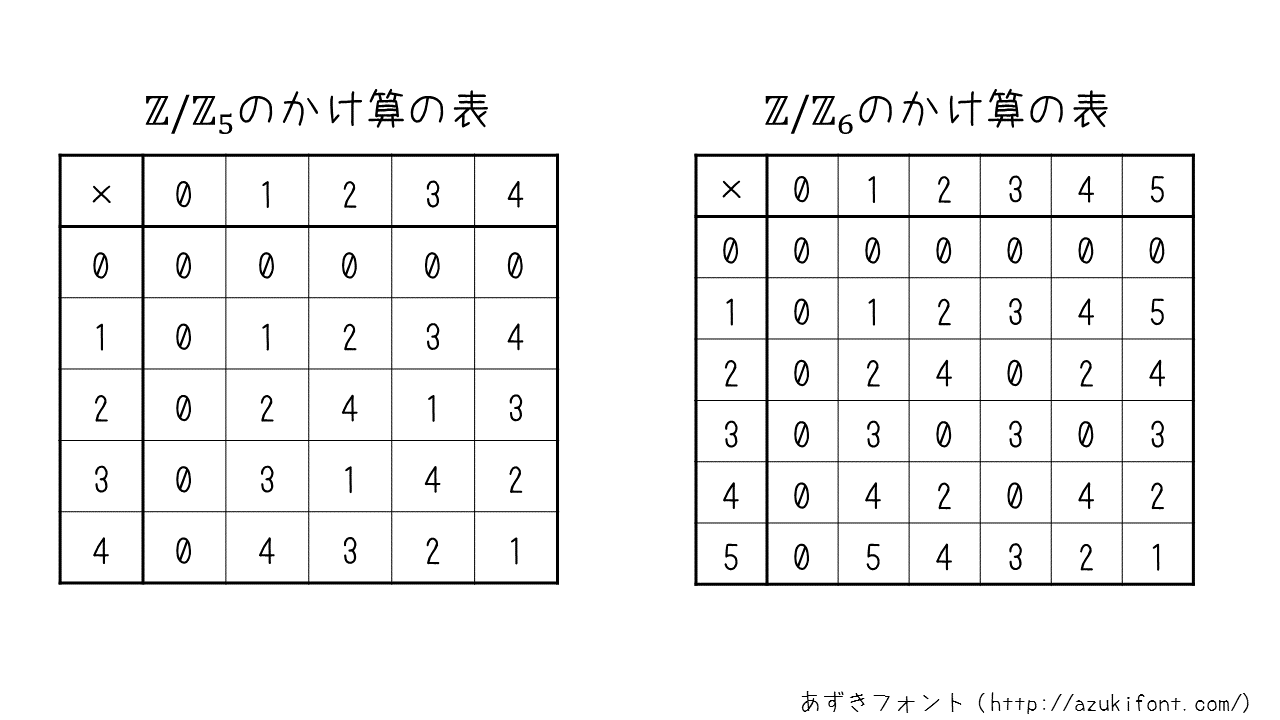
Aus dieser Tabelle haben Sie möglicherweise den Unterschied zwischen den beiden Restringen verstanden. Das heißt, in einem Restring, dessen ursprüngliche Zahl eine Primzahl ist, ist das Ergebnis der Multiplikation nicht $ \ 0 \ $, es sei denn, $ 0 \ $ wird verwendet. Daher besteht kein Grund zur Sorge, dass komplizierte Berechnungen wie die mehrfache Multiplikation aussagekräftige Berechnungen wie Ver- und Entschlüsselung aufgrund des Auftretens von $ \ 0 \ $ bedeutungslos machen können. .. In der Algebra wird der "Restring, dessen ursprüngliche Zahl eine Primzahl ist" als "endlicher Körper" bezeichnet, was in der Kryptographie nützlich ist. Zum Beispiel im Fall von $ \ mathbb {F} _ {23} \ $

\textbf{a} = \{ 2^j : j\in \{0,1,\cdots, 11\}\}.

Über den vergrößerten Körper

In der vorherigen Diskussion konnte kein endlicher Körper erstellt werden, wenn die ursprüngliche Zahl eine zusammengesetzte Zahl war. In der Tat, wenn $ n = 2 ^ 4 $,

2\times 8 = 0, 4\times4=0.

Selbst bei zusammengesetzten Zahlen kann jedoch mit dem irreduziblen Polynom ein endlicher Körper erzeugt werden. Ein irreduzibles Polynom ist ein Polynom, das nicht weiter zerlegt werden kann. Zum Beispiel

x^4 + x +1 ist ein kontrahiertes Polynom,\\
　x^4 + 1　\Ist nicht

Weil jeder Koeffizient $ \ \ {0, 1 \} \ $ ist,

x^4 + 1 = x^4 + 2x^2 + 1 = (x^2 + 1)^2.

Nun erstellen wir einen endlichen Körper. Gleichungen mit irreduziblen Polynomen: Wenn die Lösung von $ x ^ 4 + x + 1 = 0 \ $ $ \ \ alpha \ $ ist

\textbf{a} = \{ \alpha^j : j\in \{0,1,\cdots, 2^4-2\}\}

Sind alle verschiedene Originalsammlungen. Erstens unterscheiden sich die folgenden vier Elemente, da sie nicht mehr zerlegt werden können.

\alpha^0, \alpha^1, \alpha^2, \alpha^3.

Andere können mit $ \ alpha ^ 4 + \ alpha + 1 = 0 \ $ bestätigt werden.

\alpha^4 = \alpha + 1,\ \alpha^5 = \alpha^2 + \alpha, \ \alpha^6 = \alpha^3 + \alpha^2,\ \alpha^7 = \alpha^3 + \alpha + 1,\\
\alpha^8 = \alpha^2 + 1,\ \alpha^9 = \alpha^3 + \alpha,\ \alpha^{10} = \alpha^2 + \alpha + 1,\ \alpha^{11} = \alpha^3 + \alpha^2 + \alpha,\\
 \alpha^{12} = \alpha^3 + \alpha^2 + \alpha + 1,\ \alpha^{13} = \alpha^3 + \alpha^2 + 1,\ \alpha^{14} = \alpha^3 + 1,\ \alpha^{15}=1.

Wie oben erwähnt, können alle Elemente durch $ \ \ alpha ^ 0, \ alpha ^ 1, \ alpha ^ 2, \ alpha ^ 3 \ $ dargestellt werden. Wenn Sie sich die Koeffizienten von $ \ alpha ^ 3, \ alpha ^ 2, \ alpha ^ 1, \ alpha ^ 0 \ $ als Bits vorstellen,

\alpha^0 \leftrightarrow 1,\ \alpha^1\leftrightarrow 2,\ \alpha^2\leftrightarrow 4,\ \alpha^3\leftrightarrow 8,\
\alpha^4 \leftrightarrow 3,\ \alpha^5\leftrightarrow 6,\\ \alpha^6\leftrightarrow 12,\ \alpha^7\leftrightarrow 11,\
\alpha^8 \leftrightarrow 5,\ \alpha^9\leftrightarrow 10,\ \alpha^{10}\leftrightarrow 7,\\
\alpha^{11}\leftrightarrow 14,\ \alpha^{12} \leftrightarrow 15, \alpha^{13}\leftrightarrow 13,\ \alpha^{14}\leftrightarrow 9,\ \alpha^{15}\leftrightarrow 1.

Wenn wir eine arithmetische Methode erstellen können, die aus $ \ textbf {a} \ $ besteht, können wir den endlichen Körper $ \ \ mathbb {F} _ {2 ^ 4} \ $ realisieren.

Implementieren Sie eine Erweiterung

Der Galois-Körper $ \ GF (2 ^ 4) \ $ wird als vergrößerter Körper übernommen.

Quelle und Index des Galois-Körpers GF (16)

Erstellen Sie den ursprünglichen Satz von Galois $ \ GF (2 ^ 4) \ $ $ \ \ textbf {a} = (a_i) \ $ und die Indextabelle $ \ \ textbf {b} = (b_i) \ $.

 \textbf{a}= \{ 1, 2, 4, 8, 3, 6 , 12, 11, 5, 10, 7, 14, 15, 13, 9, 1\},\\
  \textbf{b}= \{0, 0, 1, 4, 2, 8, 5, 10, 3, 14, 9, 7, 6, 13, 11, 12 \}.

Ich mache mir Sorgen um $ b_0 = 0 \ $, aber es spielt keine Rolle, ob es $ \ 0 \ $ oder $ \ 100 \ $ ist, aber es entspricht trotzdem $ \ a_0 = 1, \ b_1 = 0 \ $. Ich hoffe du kannst. Das heißt, $ \ b_0 = 0 \ $ zur Vereinfachung. Sie müssen sich keine Sorgen machen.

galfield.py

# -*- coding: utf-8 -*-

def galois2(k, l):
    p = pow(2, k)
    a = [1]
    for i in range(p - 1):
        a.append(a[i] * 2)
        if a[i + 1] >= p:
            a[i + 1] = a[i + 1] - p
            a[i + 1] = a[i + 1] ^ l
    return a
 
def table2(a, k):
    b = []
    for i in range(2 ** k):
        b.append(0)
    for i in range(1, 2 ** k):
        for j in range(2 ** k - 1):
            if a[j] == i:
                b[i] = j
    return b
 
 
if __name__ == "__main__":
    # x^4 = x + 1 -> [0, 0, 1, 1] -> ll = 3
    k = 4
    ll = 3
    a = galois2(k, ll)
    b = table2(a, k)

Implementierung der Arithmetik auf dem Galois-Feld GF (16)

Zusatz

a_i + a_j := a_i \oplus a_j.

Subtraktion

a_i - a_j := a_i \oplus a_j.

Multiplizieren

a_i\times a_j:=a_{b_{a_i}+b_{a_j}} = a_{i + j\pmod{2^4-1}}.

Teilen

a_i / a_j:=a_{b_{a_i}-b_{a_j}} = a_{i - j\pmod{2^4-1}}.

Leistungsmultiplikation

a_i^n := a_{b_{a_i} \cdot n} = a_{i \cdot n\pmod{2^4-1}}.

Die Operationen, die speziell implementiert werden sollten, sind Multiplikation, Division und Leistungsmultiplikation.

galois.py

# -*- coding: utf-8 -*-
from galfield import galois2, table2

def gtimes2(k, a, b, s, t):
    return a[(b[s] + b[t]) % (2 ** k - 1)]
 
def gdiv2(k, a, b, s, t):
    return a[(b[s] - b[t]) % (2 ** k - 1)]

def gpow2(k, a, b, s, l):
    return a[(b[s] * l) % (2 ** k - 1)]
 
 
if __name__ == "__main__":
    k = 4
    ll = 3
    a = galois2(k, ll)
    b = table2(a, k)
 
# Example of caluc over galois field
# ADD & SUB
    print a[2] ^ a[5] 
# MUL & DIV
    print gtimes2(k, a, b, a[2], a[5])
    print gdiv2(k, a, b, a[2], a[5])
# POW   
    print gpow2(k, a, b, a[2], 3)

[Anhang] ElGamal-Code für die Erweiterung implementiert

Der ElGamal-Code ist ein öffentlicher Schlüsselcode, der 1984 von Taher Elgamal aus Ägypten vorgeschlagen wurde. (Es ist nicht sicher, daher denke ich, dass es wahrscheinlich nicht praktisch ist ...) Die Implementierung des ElGamal-Codes in diesem Artikel hat keine besondere Bedeutung, aber da ich den Galois-Körper implementiert habe, möchte ich ihn auf etwas anwenden. Ich habe es hier als Anhang niedergeschrieben, weil ich darüber nachgedacht habe.

Der ElGamal-Verschlüsselungsalgorithmus lautet wie folgt. (Im Allgemeinen besteht der Verschlüsselungsalgorithmus für öffentliche Schlüssel aus drei Teilen: Schlüsselgenerierung, Verschlüsselung und Entschlüsselung.) Erstens der ursprüngliche Satz von Galois $ \ GF (2 ^ 4) $ $ \ \ textbf { Erstellen Sie eine} = (a_i) \ $ und eine Indextabelle $ \ \ textbf {b} = (b_i) \ $.

• Algorithmus zur Schlüsselgenerierung
  1. x\overset{U}{\leftarrow}\\{ 0, 1, \cdots, 2^4-2\\}.
  2. h\leftarrow a_x.

3. $ x \ $ ist der private Schlüssel und $ h \ $ ist der öffentliche Schlüssel.

• Verschlüsselungsalgorithmus

1. Wählen Sie einfachen Text $ \ m \ in \ textbf {a} \ $.
2. Generieren Sie eine Zufallszahl $ \ r \ overset {U} {\ leftarrow} \ {0, 1, \ cdots, 2 ^ 4-2 \} \ $.
3. $ c_0 \ leftarrow a_r, \ c_1 \ leftarrow m \ cdot h ^ r \ $ ist die Code-Anweisung.

• Entschlüsselungsalgorithmus

1. Entschlüsselt mit $ c_1 / c_0 ^ x \ rightarrow m \ $.

gElGamal.py

# -*- coding: utf-8 -*-
from random import randint
from galfield import galois2, table2
from galois import gtimes2, gdiv2, gpow2

def GEGKeyGen(a, k):
    sk = randint(0, 2 ** k - 2)
    pk = a[sk]
    return [sk, pk]
 
def GEGEnc(m, a, pk, k):
    r = randint(0, 2 ** k - 2)
    return [a[r], gtimes2(k, a, b, m, gpow2(k, a, b, pk, r))]
 
def GEGDec(c, a, k, sk):
    return gdiv2(k, a, b, c[1], gpow2(k, a, b, c[0], sk))
 
 
if __name__ == "__main__":
    k = 4
    ll = 3
    a = galois2(k, ll)
    b = table2(a, k)
 
    m = a[2]
    key = GEGKeyGen(a, k)
    sk = key[0]
    pk = key[1]
    cipher = GEGEnc(m, a, pk, k)
    print m == GEGDec(cipher, a, k, sk) 

So implementieren Sie andere Erweiterungen ...

Ich denke, Sie sollten das irreduzible Polynom finden. Zum Beispiel verwendet AES mit allgemeiner Schlüsselverschlüsselung $ \ GF (2 ^ 8) \ $, aber sein irreduzibles Polynom ist $ \ x ^ 8 + x ^ 4 + x ^ 3 + x ^ 2 + 1 \ $. ist. Da die in der exklusiven logischen Summe von "galois2 ()" verwendeten Bits $ [0, 0, 0, 1, 1, 1, 0, 1] $ sind, ist "k = 8, ll = 29 in" galfield.py ". Sie können $ \ GF (2 ^ 8) \ $ ausdrücken, indem Sie `setzen. Wenn Sie dies bisher verstehen, können Sie meiner Meinung nach andere Erweiterungen selbst implementieren.