[PYTHON] Höchstwahrscheinlich Schätzung verschiedener Verteilungen mit Pyro
Höchstwahrscheinlich Schätzung verschiedener eindimensionaler kontinuierlicher Wahrscheinlichkeitsverteilungsparameter mit Pyro.
- Normalverteilung
- Beta-Verteilung --T Verteilung
- Platzverteilung
- Cauchy Verteilung --Exponentialverteilung
- Gammaverteilung --Gambel-Verteilung
Obwohl einige der wahrscheinlichsten Schätzungen analytische Lösungen bieten (z. B. Normalverteilung), Einige sind iterativ (z. B. Gammaverteilung). Darüber hinaus unterscheidet sich die Methode je nach Verteilung und die Implementierung ist unterschiedlich. Mach es hier mit Pyro, Definieren Sie einfach die Wahrscheinlichkeitsverteilung im Modell Danach wird die wahrscheinlichste Schätzung durch die iterative Methode mit demselben Code durchgeführt.
Nur die Normalverteilung wird im Detail erklärt. Weitere Codes finden Sie in der Übersicht unten. https://gist.github.com/tttamaki/b061f64ad1c0f640acb2bccb88b5087e
Tips
--Verwenden Sie "AutoDelta" als Richtlinie (Punktschätzung)
- Der Monitor während des Lernens ist Haken
- Schätzungen werden mit
poutine.traceeingebracht
Vorbereitung
Vorbereitung. Für Notebook
import matplotlib.pyplot as plt
%matplotlib inline
from collections import defaultdict
import os
import numpy as np
import torch
import torch.distributions.constraints as constraints
import pyro
from pyro.optim import Adam
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO
from pyro.infer.autoguide import AutoDelta, AutoNormal
from pyro.infer.autoguide.initialization import init_to_feasible
# import pyro.poutine as poutine
from pyro import poutine
pyro.enable_validation(True)
pyro.set_rng_seed(101)
from tqdm.notebook import tqdm
import daft
1-dimensionale Normalverteilung
Wahre Parameter
Erstellen Sie nach dem Zufallsprinzip true m und std
true_m = np.random.rand() * 10
true_std = np.abs(np.random.rand() * 2)
print('m =', true_m, 'std =', true_std)
x_range = np.arange(true_m - 4*true_std, true_m + 4*true_std, 0.01)
x_max = x_range.max()
x_min = x_range.min()
print('x_range: from {0:.3f} to {1:.3f}'.format(x_min, x_max))
python
m = 2.3235366181476067 std = 0.16712286732668735
x_range: from 1.655 to 2.985
Datenerstellung
Abtastdaten aus einer echten Verteilung
# sampling
target_dist = dist.Normal(true_m, true_std)
data = torch.tensor([target_dist() for i in range(100)])
#pdf: Verteilungsfunktion
true_y = [target_dist.log_prob(torch.tensor([x])).exp() for x in x_range]
fig = plt.figure(figsize=(10,5))
plt.plot(x_range, true_y, c='k', label=r'Normal(m,$\sigma$)')
plt.hist(data, range=(x_min, x_max), bins=100, density=True, alpha=0.2, label=r'observed data $\{x_i\}$')
plt.title(r'm={0:.3f} $\sigma$={1:.3f}'.format(true_m, true_std))
plt.ylim(0,)
plt.xlabel('x')
plt.legend()
plt.savefig('obs-data')
plt.show()

Die analytische Lösung der wahrscheinlichsten Schätzung ist übrigens der Mittelwert und die Varianz bei der Normalverteilung.
python
ml_m = data.numpy().mean()
ml_std = data.numpy().std()
print('m={0:.3f}, sigma={1:.3f}'.format(ml_m, ml_std))
python
m=2.318, sigma=0.157
Grafisches Modell
Das Modell "Modell" hat die folgende Struktur.
p_\theta(X) - $ X = \ {x_1, \ ldots, x_N } $ sind die beobachteten Daten
- Parameter sind $ \ theta = \ {m, \ sigma } $
x_i \sim \mathrm{Gauss}(m, \sigma)

Zeichnen Sie ein grafisches Modell mit Dummheit
pgm = daft.PGM()
pgm.add_node("xn", r"$x_n$", 2, 1, observed=True)
pgm.add_node("m", "m", 1.5, 2, fixed=True)
pgm.add_node("std", r"$\sigma$", 2.5, 2, fixed=True)
pgm.add_edge("m", "xn")
pgm.add_edge("std", "xn")
pgm.add_plate([1, 0.5, 2, 1], label=r"$n = 1, \ldots, N$", shift=-0.2)
pgm.show() # render and show
Modelle und Anleitungen
Setzen Sie für das Modell m und std als Parameter in pyro.param.
Modell-
def model(data=None):
#Der geschätzte Anfangswert ist 0.Auf 0 setzen
m = pyro.param("m", torch.tensor(0.0))
#Geschätzter Anfangswert ist 1.Auf 0 setzen
# std >Da es 0 ist, fügen Sie eine positive Einschränkung hinzu
std = pyro.param("std", torch.tensor(1.0), constraint=constraints.positive)
#Daten repräsentieren alle Daten (dh Vektorlistenarray)
with pyro.plate('observe_data'): #Da jede Beobachtung obs Unabhängigkeit voraussetzt, verwenden Sie eine Platte
pyro.sample('obs', dist.Normal(m, std), obs=data) # vector-Platte verwenden
Verwenden Sie die Punktschätzung AutoDelta als Richtlinie
python
guide = AutoDelta(
poutine.block(model, hide=['obs']), #Verstecke die Obs des Modells und benutze die anderen (m und std)
init_loc_fn=init_to_feasible #Der Anfangswert ist ein angemessener Wert
)
Geschätzte Vorbereitung
python
adam_params = {"lr": 0.005, "betas": (0.95, 0.999)}
optimizer = Adam(adam_params) #Adam vorerst
svi = SVI(model=model,
guide=guide,
optim=optimizer,
loss=Trace_ELBO()
)
Initialisieren Sie Parameter und setzen Sie Hooks. Speichern Sie den Wert in der Mitte des Parameters.
python
pyro.clear_param_store() # pyro.get_param_store()Wird leer sein
svi.loss(model, guide, data) #Ich muss das mal piro machen.get_param_store()Ist eine leere Mutter
trace_dic = defaultdict(list) #Speichern Sie den Wert (diese Liste wird hier als Trace bezeichnet)
for name, value in pyro.get_param_store().named_parameters():
print('tracing', name, type(value), value)
#Bei jeder Gradientenberechnung wird der Haken aufgerufen. Ignorieren Sie den Gradientenwert grad, verwenden Sie den Namen für param(name)Holen Sie sich den Wert mit und fügen Sie ihn der DIC-Liste hinzu
value.register_hook(lambda grad, name=name: trace_dic[name].append(pyro.param(name).item()))
python
tracing m <class 'torch.Tensor'> tensor(0., requires_grad=True)
tracing std <class 'torch.Tensor'> tensor(0., requires_grad=True)
Schätzen
Iterative Schätzung.
python
num_steps = 5000
with tqdm(range(num_steps)) as pbar:
for i,p in enumerate(pbar):
loss = svi.step(data) #Gradientenberechnung, Update
trace_dic['loss'].append(loss)
if i > 100 and np.isclose(trace_dic['loss'][-100], loss):
break #Konvergenz, wenn sich der Wert nicht von vor 100 Mal ändert
if i % 10 == 0: #Wenn Sie es jedes Mal anzeigen, ist es zu früh, um es zu sehen. Zeigen Sie es also alle 10 Mal einmal an
pbar.set_postfix(loss=loss)
Konvergenzzustand
python
fig = plt.figure(figsize=(10,5))
plt.plot(trace_dic['loss'])
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
savefig("loss")
plt.show()
fig = plt.figure(figsize=(15,5))
for i,param in enumerate(['m', 'std']):
plt.subplot(1,2,i+1)
plt.plot(trace_dic[param])
plt.ylabel(param)
plt.tight_layout()
savefig("params")
plt.show()
Zustand der Abnahme des Verlustes

Konvergenz der Parameter m und std

Ergebnis
Vergleich des wahrscheinlichsten geschätzten Wertes und des wahren Wertes
python
trace = poutine.trace(model).get_trace()
print('m', trace.nodes['m']['value'].item(), 'true m', true_m)
print('std', trace.nodes['std']['value'].item(), 'true std', true_std)
Es liegt nahe am wahren Wert.
python
m 5.083353042602539 true m 5.163986277024462
std 1.1655045747756958 true std 1.1413351737362796
Vergleich der Verteilung der wahrscheinlichsten Schätzungen und der tatsächlichen Verteilung
python
fig = plt.figure(figsize=(10,5))
#Parameter mit Trace abrufen
trace = poutine.trace(model).get_trace()
m = trace.nodes['m']['value'].item()
std = trace.nodes['std']['value'].item()
# generate a pdf
estimated_dist = dist.Normal(m, std)
y = [estimated_dist.log_prob(torch.tensor([x])).exp() for x in x_range]
# plot
plt.plot(x_range, y, c='k', label='ML estimated pdf')
plt.plot(x_range, true_y, c='r', label=r'true pdf')
plt.hist(data, range=(x_min, x_max), bins=100, alpha=0.2, density=True, l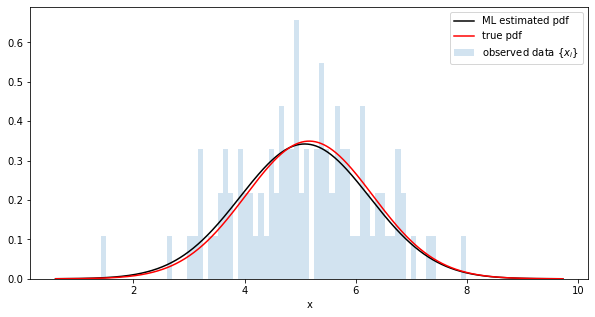
abel=r'observed data $\{x_i\}$')
plt.xlabel('x')
plt.legend()
savefig("sampled-pdf")
plt.show()

Probe aus der geschätzten Verteilung und Vergleich mit den Originaldaten
python
fig = plt.figure(figsize=(10,5))
obs = []
for _ in range(5000):
trace = poutine.trace(model).get_trace()
obs.append(trace.nodes['obs']['value'].item())
plt.xlabel('posterior samples')
plt.hist(data, range=(x_min, x_max), bins=100, alpha=0.2, density=True, label=r'observed data $\{x_i\}$')
plt.hist(obs, range=(x_min, x_max), bins=100, alpha=0.2, density=True, color='r', label=r'sampled data$')
plt.legend()
savefig("pdf-obs")
plt.show()

Andere Distributionen
Das Folgende zeigt nur die Originaldaten (blau), die wahre Verteilung (rot) und die geschätzte Verteilung mit dem wahrscheinlichsten Schätzparameter (schwarz).
Der Code ist https://gist.github.com/tttamaki/b061f64ad1c0f640acb2bccb88b5087e Es ist in.
Beta-Distribution

t Verteilung

Laplace-Verteilung

Cauchy Verteilung

Exponentialverteilung

Gammaverteilung

Gambel-Vertrieb

Recommended Posts