Hintergrund

Letztes Mal Wie finden Sie die optimale k-Zahl für k-means? Ich habe einen Artikel geschrieben ↓ Kommentarbereich

Deshalb habe ich "X-means" aktiviert.

Informationen zur X-means-Methode, mit der die Anzahl der Cluster automatisch geschätzt wird

--K-bedeutet Erweiterungsalgorithmus, vorgeschlagen von Pelleg und Moore (2000).

Bestimmen Sie automatisch die Anzahl der Cluster K.
Entwickeln Sie k-means in einen Algorithmus, der sich auch bei einer großen Anzahl von Daten mit hoher Geschwindigkeit bewegt Der Punkt ist der Unterschied zu den herkömmlichen k-Mitteln.

Die ersten beiden populären Papiere, die erscheinen, wenn Sie mit "x-means" googeln.

X-means: Extending K-means with Efficient Estimation of the Number of Clusters | Carnegie Mellon Univ. (2000)

X-bedeutet Vorschlagspapier

Erweiterung des k-means-Algorithmus, der automatisch die Anzahl der Cluster bestimmt | Forschungs- und Entwicklungsabteilung des Universitätszugangsprüfungszentrums (2000)

Japanische Arbeit
Ein Papier über eine verbesserte Version von x-means, das im selben Jahr wie das obige Originalpapier veröffentlicht wurde
Dies ist der Implementierungscode des Autors in R veröffentlicht.

x-bedeutet Übersicht

Bestimmen Sie die optimale Anzahl von Clustern unter Verwendung der Kriterien für die sequentielle Wiederholung mit k-Mitteln und die Stoppkriterien für die BIC-Teilung
Es gibt Abweichungen in der BIC-Berechnungsmethode
Die Grundidee ist die Annahme, dass die Daten in der Nähe des Schwerpunkts Gauß-verteilt sind.
Da das Konzept der Wahrscheinlichkeitsverteilung eingeführt und das Konzept der Wahrscheinlichkeit daraus geboren wird, --Fließen Sie, dass der BIC berechnet werden kann

--x-means ruft rekursiv auf und verwendet k-means

Die Nachteile von k-Mitteln (Anfangswertabhängigkeit) werden gezogen.
Der Cluster ändert sich nach und nach mit jeder Berechnung
Die Clustergröße ist jedoch stabil, sodass sie als Richtlinie für die optimale Anzahl von Clustern verwendet werden kann.

--Wenn keine vorherigen Testinformationen vorliegen, kann die optimale Anzahl von Clustern mit einem Berechnungsbetrag erhalten werden, der unabhängig von der Erkennungsmethode mehr als doppelt so hoch ist wie der von k-means.

Berechnungsablauf

Der grobe Fluss ist

K-Mittel mit einer kleinen Anzahl von Clustern
2-bedeutet den resultierenden Cluster, teilen Sie den Cluster,
Wenn der BIC wächst, übernehmen Sie
Kehren Sie zu 2 zurück

Abb. Zitat aus 1 Papier

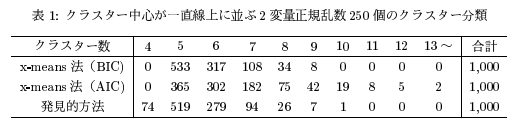
(Zitiert aus dem Papier) Genauigkeitsvergleich, wenn die Anzahl der richtigen Cluster 5 beträgt ――Die Anzahl der richtigen Cluster ist bei der Auswertung durch BIC größer als durch AIC. --AIC neigt dazu, eine relativ große Anzahl von Clustern zu erzeugen
Das Ergebnis der Erkennungsmethode (die Methode zur manuellen Angabe der k-Zahl mit k-Mitteln) liegt nahe am Ergebnis des BIC (wenn es mit dem manuell erhaltenen Ergebnis übereinstimmt, ist x-Mittelwert, das dies automatisch tut, besser! )

Unterschied in der Logik zwischen den beiden Papieren

Umriss des Originalpapiers von 1

Nehmen Sie implizit an, dass alle Cluster die gleiche Datenverteilung haben

Zusammenfassung von 2 verbesserten Logikpapieren

――Der Schwerpunkt sollte je nach Größe des Clusters unterschiedlich sein. Daher erstellen wir eine Logik, um dies ebenfalls abzuschätzen.

Andere Blog-Beiträge über x-means:

Implementierte die x-means-Methode in Python
x-means (Im OpenCV-Beispiel ein Artikel, der die Verarbeitung von Farbreduktion / Bildteilung mit k-means durch x-means ersetzt. )
x-means-Methode
R de k-means-Methode und ihre Erweiterung 2 x-means edition | Sabotage verbotenes Tagebuch

X-bedeutet Skript in Python

Implementierte die x-means-Methode in Python [Gist Code] / yasaichi / 254a060eff56a3b3b858)

# -*- coding: utf-8 -*-
import numpy as np
from scipy import stats
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from IPython.display import display, HTML #Für Jupyter Notebook
%matplotlib inline

class XMeans:
    """
    x-Klasse, die die Mittelwertmethode ausführt
    """

    def __init__(self, k_init = 2, **k_means_args):
        """
        k_init : The initial number of clusters applied to KMeans()
        """
        self.k_init = k_init
        self.k_means_args = k_means_args

    def fit(self, X):
        """
        x-Clusterdaten X mit der Methode means
        X : array-like or sparse matrix, shape=(n_samples, n_features)
        """
        self.__clusters = [] 

        clusters = self.Cluster.build(X, KMeans(self.k_init, **self.k_means_args).fit(X))
        self.__recursively_split(clusters)

        self.labels_ = np.empty(X.shape[0], dtype = np.intp)
        for i, c in enumerate(self.__clusters):
            self.labels_[c.index] = i

        self.cluster_centers_ = np.array([c.center for c in self.__clusters])
        self.cluster_log_likelihoods_ = np.array([c.log_likelihood() for c in self.__clusters])
        self.cluster_sizes_ = np.array([c.size for c in self.__clusters])

        return self

    def __recursively_split(self, clusters):
        """
Teilen Sie die Argumentcluster rekursiv auf
        clusters : list-like object, which contains instances of 'XMeans.Cluster'
        'XMeans.Cluster'Listentypobjekt, das eine Instanz von enthält
        """
        for cluster in clusters:
            if cluster.size <= 3:
                self.__clusters.append(cluster)
                continue

            k_means = KMeans(2, **self.k_means_args).fit(cluster.data)
            c1, c2 = self.Cluster.build(cluster.data, k_means, cluster.index)
           
            beta = np.linalg.norm(c1.center - c2.center) / np.sqrt(np.linalg.det(c1.cov) + np.linalg.det(c2.cov))
            alpha = 0.5 / stats.norm.cdf(beta)
            bic = -2 * (cluster.size * np.log(alpha) + c1.log_likelihood() + c2.log_likelihood()) + 2 * cluster.df * np.log(cluster.size)

            if bic < cluster.bic():
                self.__recursively_split([c1, c2])
            else:
                self.__clusters.append(cluster)

    class Cluster:
        """
        k-Eine Klasse, die Informationen über den durch die Mittelmethode generierten Cluster enthält und die Wahrscheinlichkeit und den BIC berechnet.
        """

        @classmethod
        def build(cls, X, k_means, index = None): 
            if index == None:
                index = np.array(range(0, X.shape[0]))
            labels = range(0, k_means.get_params()["n_clusters"])  

            return tuple(cls(X, index, k_means, label) for label in labels) 

        # index:Ein Vektor, der zeigt, zu welcher Zeile der Originaldaten die Stichprobe in jeder Zeile von X gehört
        def __init__(self, X, index, k_means, label):
            self.data = X[k_means.labels_ == label]
            self.index = index[k_means.labels_ == label]
            self.size = self.data.shape[0]
            self.df = self.data.shape[1] * (self.data.shape[1] + 3) / 2
            self.center = k_means.cluster_centers_[label]
            self.cov = np.cov(self.data.T)

        def log_likelihood(self):
            return sum(stats.multivariate_normal.logpdf(x, self.center, self.cov) for x in self.data)

        def bic(self):
            return -2 * self.log_likelihood() + self.df * np.log(self.size)

if __name__ == "__main__":
    import matplotlib.pyplot as plt

    #Datenaufbereitung
    x = np.array([np.random.normal(loc, 0.1, 20) for loc in np.repeat([1,2], 2)]).flatten() #Generieren Sie 80 Zufallszahlen
    y = np.array([np.random.normal(loc, 0.1, 20) for loc in np.tile([1,2], 2)]).flatten() #Generieren Sie 80 Zufallszahlen

    #Clustering durchführen
    x_means = XMeans(random_state = 1).fit(np.c_[x,y])  
    print(x_means.labels_)
    print(x_means.cluster_centers_)
    print(x_means.cluster_log_likelihoods_)
    print(x_means.cluster_sizes_)

    #Zeichnen Sie die Ergebnisse
    plt.rcParams["font.family"] = "Hiragino Kaku Gothic Pro"
    plt.scatter(x, y, c = x_means.labels_, s = 30)
    plt.scatter(x_means.cluster_centers_[:,0], x_means.cluster_centers_[:,1], c = "r", marker = "+", s = 100)
    plt.xlim(0, 3)
    plt.ylim(0, 3)
    plt.title("x-means_test1")
    plt.legend()
    plt.grid()
    plt.show()
    # plt.savefig("clustering.png ", dpi = 200)

[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2]
[[ 1.01854145  2.00982242]
 [ 1.00199794  1.02110352]
 [ 2.00022392  2.00435037]
 [ 2.04408807  1.0518478 ]]
[ 42.91288569  44.48049658  37.32131967  29.6422041 ]
[20 20 20 20]

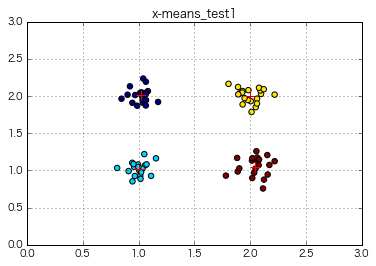
⇒ X-means wurde an den Daten von 4 Clustern durchgeführt und sicherlich in 4 Cluster unterteilt, ohne eine explizite k-Zahl anzugeben!

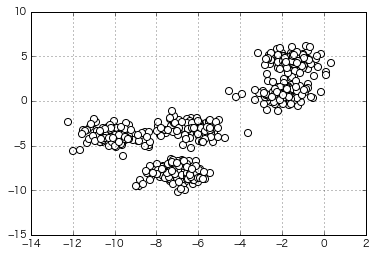
Versuchen Sie, Daten zu gruppieren, die etwas ähnlicher aussehen

(Die Anzahl der zum Zeitpunkt der Generierung angegebenen Cluster beträgt 5)

from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500,
                  n_features=2,
                  centers=5,
                  cluster_std=0.8,
                  center_box=(-10.0, 10.0),
                  shuffle=True,
                  random_state=1)  # For reproducibility

x =X[:,0]
y =X[:,1]
X=np.c_[x,y]

plt.scatter(x,y,c='white',marker='o',s=50)
plt.grid()
plt.show()

if __name__ == "__main__":
    import matplotlib.pyplot as plt

    #Clustering durchführen
    x_means = XMeans(random_state = 1).fit(np.c_[X])  

    #Zeichnen Sie die Ergebnisse
    plt.rcParams["font.family"] = "Hiragino Kaku Gothic Pro"
    plt.scatter(x, y, c = x_means.labels_, s = 30)
    plt.scatter(x_means.cluster_centers_[:,0], x_means.cluster_centers_[:,1], c = "r", marker = "*", s = 250)
    plt.title("x-means_test2")
    plt.grid()
    plt.show()

⇒ Dies ist auch richtig aufgeteilt!

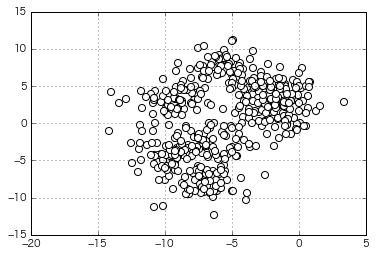
Versuchen Sie, mehr launische Daten zu gruppieren

(Die Anzahl der zum Zeitpunkt der Generierung angegebenen Cluster beträgt 8)

from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500,
                  n_features=2,
                  centers=8,
                  cluster_std=1.5,
                  center_box=(-10.0, 10.0),
                  shuffle=True,
                  random_state=1)  # For reproducibility

x =X[:,0]
y =X[:,1]
X=np.c_[x,y]

plt.scatter(X[:,0],X[:,1],c='white',marker='o',s=50)
plt.grid()
plt.show()

if __name__ == "__main__":
    import matplotlib.pyplot as plt

    #Clustering durchführen
    x_means = XMeans(random_state = 1).fit(np.c_[X])  

    #Zeichnen Sie die Ergebnisse
    plt.rcParams["font.family"] = "Hiragino Kaku Gothic Pro"
    plt.scatter(x, y, c = x_means.labels_, s = 30)
    plt.scatter(x_means.cluster_centers_[:,0], x_means.cluster_centers_[:,1], c = "r", marker = "*", s = 250)
    plt.title("x-means_test3")
    plt.grid()
    plt.show()

=> Beim automatischen Clustering mit x-means wird die optimale Anzahl von Clustern mit "5" berechnet. Es fühlt sich geteilt an.

Ich werde versuchen, wieder ein Ellbogenbuch ohne sexuelle Disziplin zu schreiben

Informationen zum Lesen des Ellbogendiagramms finden Sie unter Vorheriger Artikel. (Geben Sie die Summe der quadratischen Fehler in den Clustern 1 bis 10 zusammen aus.)

distortions = []

for i  in range(1,11):                # 1~Berechnen Sie bis zu 10 Cluster gleichzeitig
    km = KMeans(n_clusters=i,         #Anzahl der Cluster
                init='k-means++',     # k-means++Wählen Sie das Cluster-Center nach Methode aus
                n_init=10,            #K mit unterschiedlichen Anfangswerten der Schwerpunkte-bedeutet Standardausführungsanzahl: '10'Wählen Sie das Modell mit dem kleineren SSE-Wert als endgültiges Modell aus
                max_iter=300,         # k-bedeutet Maximale Anzahl von Iterationen innerhalb des Standardalgorithmus: '300'
                random_state=0)       #Status des Zufallszahlengenerators, der zum Initialisieren des Schwerpunkts verwendet wird
    km.fit(X)                         #Führen Sie Clusterberechnungen durch
    distortions.append(km.inertia_)   # km.fit und km.inertia_Ist gesucht
    y_km = km.fit_predict(X)
    
plt.plot(range(1,11),distortions,marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()

=> Es ist immer noch schwierig, die optimale Anzahl von Clustern anhand dieser Zahl als "5" zu beurteilen.

Ich werde versuchen, wieder ein Silhouette-Buch ohne sexuelle Disziplin zu schreiben

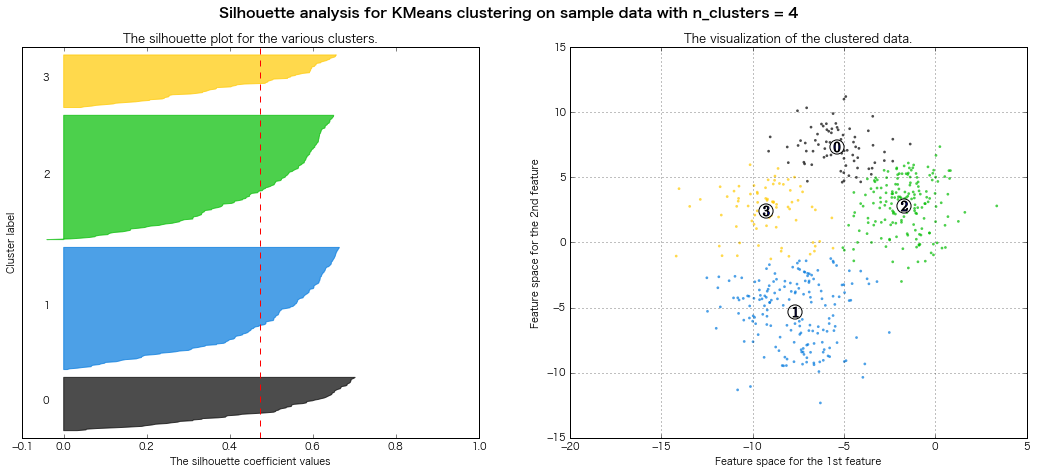
Informationen zum Lesen des Silhouettendiagramms finden Sie unter Vorheriger Artikel. (Geben Sie die Silhouettendiagramme der Cluster 3 bis 8 zusammen aus.)

Leihen Sie den Code von [offizielle Seite von scikit-learn] aus (http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html#example-cluster-plot-kmeans-silhouette-analysis-py%5D). Teilweise umgeschrieben)

km = KMeans(n_clusters=5,       #Anzahl der Cluster
            init='k-means++',   # k-means++Wählen Sie das Cluster-Center nach Methode aus
            n_init=10,          #K mit unterschiedlichen Anfangswerten der Schwerpunkte-bedeutet Standardausführungsanzahl: '10'Wählen Sie das Modell mit dem kleineren SSE-Wert als endgültiges Modell aus
            max_iter=300,       # k-bedeutet Maximale Anzahl von Iterationen innerhalb des Standardalgorithmus: '300'
            random_state=0)     #Status des Zufallszahlengenerators, der zum Initialisieren des Schwerpunkts verwendet wird
y_km = km.fit_predict(X)

from __future__ import print_function

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score

import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np

print(__doc__)

# Generating the sample data from make_blobs

X, y = make_blobs(n_samples=500,
                  n_features=2,
                  centers=8,
                  cluster_std=1.5,
                  center_box=(-10.0, 10.0),
                  shuffle=True,
                  random_state=1)  # For reproducibility

range_n_clusters = [3, 4, 5, 6, 7, 8]

for n_clusters in range_n_clusters:
    # Create a subplot with 1 row and 2 columns
    fig, (ax1, ax2) = plt.subplots(1, 2)
    fig.set_size_inches(18, 7)

    # The 1st subplot is the silhouette plot
    # The silhouette coefficient can range from -1, 1 but in this example all
    # lie within [-0.1, 1]
    ax1.set_xlim([-0.1, 1])
    # The (n_clusters+1)*10 is for inserting blank space between silhouette
    # plots of individual clusters, to demarcate them clearly.
    ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])

    # Initialize the clusterer with n_clusters value and a random generator
    # seed of 10 for reproducibility.
    clusterer = KMeans(n_clusters=n_clusters, random_state=1)
    cluster_labels = clusterer.fit_predict(X)

    # The silhouette_score gives the average value for all the samples.
    # This gives a perspective into the density and separation of the formed
    # clusters
    silhouette_avg = silhouette_score(X, cluster_labels)
    print("For n_clusters =", n_clusters,
          "The average silhouette_score is :", silhouette_avg)

    # Compute the silhouette scores for each sample
    sample_silhouette_values = silhouette_samples(X, cluster_labels,metric='euclidean')

    y_lower = 10
    for i in range(n_clusters):
        # Aggregate the silhouette scores for samples belonging to
        # cluster i, and sort them
        ith_cluster_silhouette_values = \
            sample_silhouette_values[cluster_labels == i]

        ith_cluster_silhouette_values.sort()

        size_cluster_i = ith_cluster_silhouette_values.shape[0]
        y_upper = y_lower + size_cluster_i

        color = cm.spectral(float(i) / n_clusters)
        ax1.fill_betweenx(np.arange(y_lower, y_upper),
                          0, ith_cluster_silhouette_values,
                          facecolor=color, edgecolor=color, alpha=0.7)

        # Label the silhouette plots with their cluster numbers at the middle
        ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))

        # Compute the new y_lower for next plot
        y_lower = y_upper + 10  # 10 for the 0 samples

    ax1.set_title("The silhouette plot for the various clusters.")
    ax1.set_xlabel("The silhouette coefficient values")
    ax1.set_ylabel("Cluster label")

    # The vertical line for average silhoutte score of all the values
    ax1.axvline(x=silhouette_avg, color="red", linestyle="--")

    ax1.set_yticks([])  # Clear the yaxis labels / ticks
    ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])

    # 2nd Plot showing the actual clusters formed
    colors = cm.spectral(cluster_labels.astype(float) / n_clusters)
    ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
                c=colors)

    # Labeling the clusters
    centers = clusterer.cluster_centers_
    # Draw white circles at cluster centers
    ax2.scatter(centers[:, 0], centers[:, 1],
                marker='o', c="white", alpha=1, s=200)

    for i, c in enumerate(centers):
        ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1, s=100)

    ax2.set_title("The visualization of the clustered data.")
    ax2.set_xlabel("Feature space for the 1st feature")
    ax2.set_ylabel("Feature space for the 2nd feature")

    plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
                  "with n_clusters = %d" % n_clusters),
                 fontsize=14, fontweight='bold')
    plt.grid()
    plt.show()

Automatically created module for IPython interactive environment
For n_clusters = 3 The average silhouette_score is : 0.500273979793

For n_clusters = 4 The average silhouette_score is : 0.473805434223

For n_clusters = 5 The average silhouette_score is : 0.451524016461

For n_clusters = 6 The average silhouette_score is : 0.428239776719

For n_clusters = 7 The average silhouette_score is : 0.427688325647

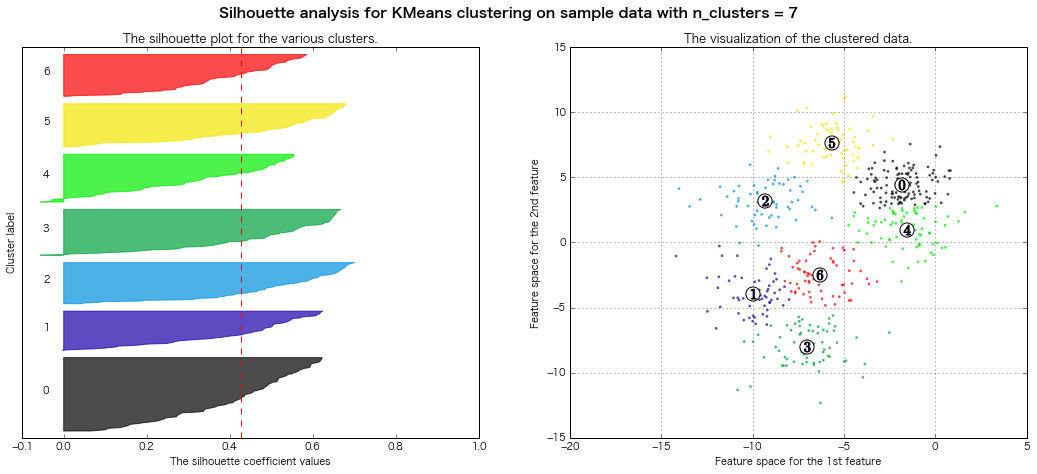
For n_clusters = 8 The average silhouette_score is : 0.409792863353

=> Bewertung des Silhouettendiagramms Rechtlich gesehen scheinen 7 oder 8 Cluster gut zu sein.

Fazit

--x-means scheint sich sicherlich gut zu sammeln ――Jedoch gibt es keine Möglichkeit, die Anzahl der Cluster "abzugleichen", und wird es immer noch verwendet, um eine "Richtlinie" für die optimale Anzahl von Clustern zu erhalten? " ――Es ist immer noch schwierig, eine Schätzung der optimalen Anzahl von Clustern aus dem Ellbogendiagramm zu erhalten ...?

Gleich für die Silhouette-Methode ...

⇒ Fühlt es sich schließlich so an, als würde man einen Cluster auswählen, der je nach Clustering-Zweck leicht zu interpretierende Ergebnisse liefert?

Anhang (Ich habe verschiedene Dinge recherchiert, um den Inhalt zu verstehen)

Lassen Sie uns die Logik der x-means-Methode untersuchen! → Ich kenne den Basian Information Bount Standard (BIC) nicht → Ich kenne AIC überhaupt nicht richtig → Wahrscheinlichkeit ist Was ist es schließlich? → Es gibt eine andere Bayes'sche Schätzung als die wahrscheinlichste, um die Wahrscheinlichkeit zu ermitteln ... Von dort aus endlos weitermachen Yak-Rasur

"Acutally, my whole life is just one big yak shaving exercise." - Joi Ito

Akaike-Informationskriterium: AIC (Akaikes Informationskriterium)

Anzeige zur Auswahl eines Modells mit der optimalen Anzahl von Parametern

――Das für bestimmte Daten erstellte Modell kann durch Erhöhen der Parameter besser mit den vorhandenen Daten kompatibel sein, es kommt jedoch zu einem Übertraining. ――Es ist notwendig, die Anzahl der Modellierungsparameter zu reduzieren, um nicht in Übertraining zu geraten, aber es ist ein schwieriges Problem, die Anzahl tatsächlich zu reduzieren.

Wenn Sie AIC mit einem Modell berechnen und den ** Mindestwert ** anzeigen, wird häufig eine gute Modellauswahl getroffen ―― Da sich AIC aus der logarithmischen Wahrscheinlichkeit des Modells und der Anzahl der Parameter zusammensetzt, kann der Kompromiss zwischen Genauigkeit und Komplexität gut beschrieben werden.

AIC = -2 \ ln {} L + 2k

Der erste Term der Gleichung repräsentiert die gute Anpassung an das Modell, und der zweite Term repräsentiert die Strafe für die Komplexität des Modells.
Im zweiten Term kann das Überanpassungsproblem umso mehr vermieden werden, je kleiner die Anzahl der Parameter ist, sodass es für das Modell mit einer geringeren Anzahl von Parametern besser funktioniert. ――Selbst wenn die Passform gut ist, ist ein durcheinandergebrachtes kompliziertes Modell nicht vorzuziehen, daher ein Index, der gut passt und auf ein einfaches Modell abzielt ――Es kann gesagt werden, dass ein gutes Modell im Allgemeinen ausgewählt werden kann, indem der AIC für alle Zielmodelle berechnet und das kleinste Modell ausgewählt wird.

Referenz:

Bayesianisches Informationskriterium (BIC)

In vielen Fällen kann eine gute Modellauswahl getroffen werden, wenn der BIC den Mindestwert anzeigt.
Im Vergleich zu AIC ein Index, der Stichprobengröße und -größe als Nachteil für die Komplexität des Modells in Abschnitt 2 betrachtet.
Im Gegensatz zu AIC ist die Auswahl nach diesem Kriterium konsistent (eine große Anzahl von Stichproben führt zu einer wahren Reihenfolge).

BIC = -2 \ ln {} L + k \ cdot \ ln {(n)}

Referenz: Bayesian Information Criterion | wikipedia

Unterschied zwischen AIC und BIC

Unterschiedlicher Zweck
Verwenden Sie AIC, wenn Sie ein Modell auswählen möchten, um die Vorhersagegenauigkeit zu verbessern
Verwenden Sie BIC, wenn Sie die Struktur kennen möchten, aus der die Daten generiert werden
Mathematischer Unterschied
Strafpunkt in Absatz 2 ――In AIC wird das Gewicht des ersten Terms groß, wenn die Stichprobengröße unabhängig von der Stichprobengröße groß ist, und es wird tendenziell ein kompliziertes Modell ausgewählt.
Bei BIC wird die Stichprobengröße bei den Strafen berücksichtigt, sodass in der Regel ein einfacheres Modell als AIC ausgewählt wird.
Unterschied in der Schätzstrategie der Modellparameter --AIC bestimmt den Maximalwert der Wahrscheinlichkeitsfunktion durch Schätzung der maximalen Wahrscheinlichkeit --BIC bestimmt den Maximalwert der Wahrscheinlichkeitsfunktion durch Bayes'sche Schätzung

―― Es besteht jedoch kein Konsens darüber, dass es auf diese Weise verwendet werden muss.

Referenz:

Akaike Informationsmenge Standard AIC und Bayes Informationsmenge Standard BIC | Sag es mir! Goo
[Bayes Information Amount Criteria und seine Entwicklungsübersicht- | ALBERT Official Blog](http://blog.albert2005.co.jp/2016/04/19/%E3%83%99%E3%82%A4% E3% 82% BA% E6% 83% 85% E5% A0% B1% E9% 87% 8F% E8% A6% 8F% E6% BA% 96% E5% 8F% 8A% E3% 81% B3% E3% 81% 9D% E3% 81% AE% E7% 99% BA% E5% B1% 95-% EF% BD% 9E% E6% A6% 82% E8% AA% AC% E7% B7% A8% EF% BD % 9E /)

Überprüfung der Wahrscheinlichkeit

Bewertung von "Wie hoch war die Wahrscheinlichkeit überhaupt?"

Die Plausibilität des Modells unter Berücksichtigung der erhaltenen Daten wird als Plausibilität bezeichnet. Quelle

Das Grundkonzept der Likelihood-Funktion besteht darin, die Frage zu beantworten ** "Aus welchen Parametern stammen die Daten nach dem Abtasten und Beobachten der Daten ursprünglich?" ** ist. Quelle

Wahrscheinlichkeit ist genau wie Wahrscheinlichkeit. Die Denkweise ist jedoch anders. Für die Wahrscheinlichkeit sind die Parameter fest und die Daten ändern sich, für die Wahrscheinlichkeit sind die Daten fest und die Parameter ändern sich. Quelle

Referenz:

Was ist die wahrscheinlichste Schätzung?

Wenn die Wahrscheinlichkeit maximal ist = Kennen Sie die Parameter (Mittelwert und Varianz bei der Gaußschen Verteilung) des Modells, das Sie schätzen möchten (Wahrscheinlichkeitsverteilung: im Grunde Gaußsche Verteilung)

Unterschied zwischen der wahrscheinlichsten Schätzung und der Bayes'schen Schätzung

	ist, was?	Methode	Mit anderen Worten
Höchstwahrscheinlich Schätzung	Wahrscheinlichkeit maximierenSo berechnen Sie die Parameter	Nur WahrscheinlichkeitSchätzen Sie die Parameter mit (denken Sie nicht an die vorherige Wahrscheinlichkeit)	Schätzen Sie die Parameter nur anhand der Wahrscheinlichkeit der gerade erfassten Daten
Bayesianische Schätzung	Maximieren Sie die hintere WahrscheinlichkeitSo berechnen Sie die Parameter	Vorwahrscheinlichkeit und WahrscheinlichkeitSchätzen Sie die Parameter mit beiden	Schätzen Sie die Parameter nicht nur anhand der gerade erfassten Daten, sondern auch anhand der Vor- und Nachwahrscheinlichkeit

Referenz:

Welches sollte ich verwenden, die wahrscheinlichste Schätzung oder die Bayes'sche Schätzung?

(grob gesagt) Beide sind im Grunde gleich
Der größte Unterschied ist ** ob "Vorwahrscheinlichkeit" berücksichtigt werden soll **
Die wahrscheinlichste Schätzung berücksichtigt nicht die vorherige Wahrscheinlichkeit (= es kann gesagt werden, dass eine gleichmäßige Verteilung angenommen wird). Mit anderen Worten, der Start erfolgt, wenn keine Informationen vorliegen.
Wenn die vorherigen Wahrscheinlichkeiten nicht einheitlich sind, unterscheiden sich die Ergebnisse der wahrscheinlichsten Schätzung und der Bayes'schen Schätzung.
Bei der Bayes'schen Schätzung kann eine genauere Schätzung durchgeführt werden, wenn die optimale vorherige Wahrscheinlichkeit eingestellt werden kann.
Die Bayes-Schätzung ist eine Schätzung, bei der mehr Informationen verwendet werden.
Die Einstellung vor der Wahrscheinlichkeit ist in der Regel subjektiv. Dies scheint das Zentrum der Kontroverse zwischen dem wahrscheinlichsten und dem Bayesianischen zu sein
Insbesondere wenn keine Vorhersage im Voraus vorliegt oder die optimale vorherige Verteilung nicht bekannt ist, wird eine vorherige Verteilung verwendet, die als "keine Informationsverteilung" bezeichnet wird (viele Programme verwenden standardmäßig keine Informationsverteilung).

Referenz: Unterschied zwischen konventioneller Schätzmethode und Bayes'scher Schätzmethode | Sonnenseite nach oben!

Über die Bayes'sche Schätzung

Ein typischer Indikator für die Eignung der Bayes'schen Schätzung ist der ** Bayes'sche Faktor (BF) ** --BF repräsentiert das ** Likelihood Ratio ** der beiden Modelle --BF kann an BIC (Bayes Information Quantity Standard) angenähert werden.

Unterschied im BIC zwischen den beiden Modellen ≒ doppelt so logarithmisch wie BF (* Beachten Sie, dass sie unterschiedlich sind, nur weil sie ähnlich sind)

Wenn Modell M_0 mit Hypothese H_0 und Modell M_1 mit Hypothese H_1 existieren,

\frac{P(H_1|D)}{P(H_0|D)}=\frac{P(D|H_1)P(H_1)}{P(D|H_0)P(H_0)} \cdots ①

\frac{P(D|H_1)P(H_1)}{P(D|H_0)P(H_0)}=\frac{P(D|H_1)}{P(D|H_0)}×\frac{P(H_1)}{P(H_0)} \cdots ②

von

\frac{P(D|H_1)}{P(D|H_0)} = \frac{P(H_1|D)}{P(H_0|D)} × \frac{P(H_0)}{P(H_1)}

oder

Wahrscheinlichkeitsverhältnis (Bayes-Faktor) = Ex-post-Wahrscheinlichkeitsverhältnis × Pre-Wahrscheinlichkeitsverhältnis

Referenz: Bayes-Faktor und Modellauswahl | SlideShare

Bayes-Faktor-Kriterien

BF	2logBF (≒BIC)	Beurteilung für M1 im Vergleich zu M0
BF<1	2logBF<0	M0 ist besser
1<BF<3	0<2logBF<2	M1 ist kaum besser
3<BF<12	2<2logBF<5	M1 ist besser (positiv)
12<BF<150	5<2logBF<10	M1 ist viel besser (stark)
150<BF	10<2logBF	M1 ist viel besser (sehr stark)

Vorteile und Probleme der Verwendung des Bayes'schen Faktors für die Modellbewertung

■ Vorteile

Befreien Sie sich vom Fluch der Nullhypothese
Der traditionelle Test besteht aus "Nullhypothese" und "Gegenhypothese". ――Aber wenn es sich um den Bayes-Faktor handelt, vergleichen Sie einfach "zwei unabhängige Modelle (Hypothese)".
Es besteht keine Notwendigkeit für eine "Nullhypothese"
Frei vom Fluch der Normalverteilung
Die Bayes'sche Gleichung enthält eine vorherige Verteilung ―― „Die vorherige Verteilung muss keine Normalverteilung sein“ → Sie kann durch Anwendung eines flexibleren statistischen Modells untersucht werden. ・・・ Die Bayes'sche Schätzung wird verwendet

■ Probleme

Der Bayes-Faktor ist das "Wahrscheinlichkeitsverhältnis" der beiden Modelle ――Die Größe des numerischen Werts kann nur "Vergleichen Sie die beiden und was ist besser" sein. ――Es ist gut, mehrere Indikatoren zu berechnen und insgesamt zu denken
Die Berechnung ist schwierig ――Es wird aufgrund der Erhöhung der Parameter und der vorherigen Verteilung schwierig.

Weitere Vor- und Nachteile der Bayes'schen Schätzung finden Sie unter hier.

Andere, die als Index (Referenz) für die Auswahl des am besten geeigneten Modells dienen

Abweichungsinformationskriterium (DIC)
Post-Mortem-P-Wert
Das Problem bei Indikatoren wie AIC und BIC besteht darin, dass sie nicht auf einzelne Modelle angewendet werden können, die latente Variablen enthalten. ――Es scheint auch eine Menge an Informationen wie FIC (Factorized Information Criterion) und FAB (Factorized Asymptotic Bayesian Inference) zu geben, um diese zu behandeln.

Referenz: [Papier] Eine kurze Zusammenfassung des Lernens heterogener Mischungen | Feces Net Benkei

[PYTHON] Ich habe die X-Means-Methode untersucht, mit der die Anzahl der Cluster automatisch geschätzt wird

Hintergrund

Informationen zur X-means-Methode, mit der die Anzahl der Cluster automatisch geschätzt wird

Die ersten beiden populären Papiere, die erscheinen, wenn Sie mit "x-means" googeln.

x-bedeutet Übersicht

Berechnungsablauf

Abb. Zitat aus 1 Papier

Unterschied in der Logik zwischen den beiden Papieren

Umriss des Originalpapiers von 1

Zusammenfassung von 2 verbesserten Logikpapieren

X-bedeutet Skript in Python

Versuchen Sie, Daten zu gruppieren, die etwas ähnlicher aussehen

Versuchen Sie, mehr launische Daten zu gruppieren

Ich werde versuchen, wieder ein Ellbogenbuch ohne sexuelle Disziplin zu schreiben

Ich werde versuchen, wieder ein Silhouette-Buch ohne sexuelle Disziplin zu schreiben

Fazit

Anhang (Ich habe verschiedene Dinge recherchiert, um den Inhalt zu verstehen)

Akaike-Informationskriterium: AIC (Akaikes Informationskriterium)

Bayesianisches Informationskriterium (BIC)

Unterschied zwischen AIC und BIC

Überprüfung der Wahrscheinlichkeit

Was ist die wahrscheinlichste Schätzung?

Unterschied zwischen der wahrscheinlichsten Schätzung und der Bayes'schen Schätzung

Welches sollte ich verwenden, die wahrscheinlichste Schätzung oder die Bayes'sche Schätzung?

Über die Bayes'sche Schätzung

Bayes-Faktor-Kriterien

Vorteile und Probleme der Verwendung des Bayes'schen Faktors für die Modellbewertung

Andere, die als Index (Referenz) für die Auswahl des am besten geeigneten Modells dienen