[PYTHON] Korrelationskoeffizient MIC, der nichtlineare Beziehungen verarbeiten kann, und Hilbert-Schmidt-Unabhängigkeitstest HSIC

Der Pearson-Korrelationskoeffizient ist ein bekannter Index zur Messung der Unabhängigkeit von Variablen. Es handelt sich jedoch um einen Index, der sich mit linearen (linearen) Beziehungen befasst, und wenn eine U-förmige Beziehung wie eine quadratische Funktion vorliegt, wird er als "keine Korrelation" beurteilt. MIC und HSIC sind als Indikatoren für den Umgang mit solchen nichtlinearen Beziehungen bekannt, daher habe ich versucht, das Python-Paket zu verwenden.

Der gesamte unten stehende Code wurde mit Google Colaboratory getestet.

Python-Paket zur Berechnung des maximalen Informationskoeffizienten (MIC)

Sie können die Installation wie folgt durchführen:

!pip install minepy

Bereiten Sie sich nach der Installation wie folgt vor.

from minepy import MINE
mine = MINE()

Python-Paket zur Berechnung des HSIC (Hilbert-Schmidt Independence Criterion)

Git-Klon wie folgt:

!git clone https://github.com/amber0309/HSIC.git

Bereiten Sie wie folgt vor.

from HSIC.HSIC import hsic_gam

Lineare Funktion

Lassen Sie uns zunächst die lineare Funktion untersuchen.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

X = np.linspace(-1, 1, 51)
Y = X
plt.scatter(X, Y)

out6.png

Der Pearson-Korrelationskoeffizient ist

np.corrcoef(X, Y)[0, 1]

1.0

MIC ist

mine.compute_score(X, Y)
mine.mic()

0.9999999999999998

Je größer der nächste Wert ist, desto geringer ist die Unabhängigkeit von HSSC, und je kleiner der Wert ist, desto höher ist die Unabhängigkeit.

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

22.610487654066624

Fügen wir der linearen Funktion Rauschen hinzu.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = X + np.random.rand(51,)
plt.scatter(X, Y)

out10.png

Der Pearson-Korrelationskoeffizient ist

np.corrcoef(X, Y)[0, 1]

0.9018483832673769

MIC ist

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

13.706487127525389

Berechnen wir, wie sich der Pearson-Korrelationskoeffizient ändert, wenn das Rauschen nach und nach zunimmt.

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X + np.random.rand(51,) * d / 10
    D.append(d)
    C.append(np.corrcoef(X, Y)[0, 1])

plt.plot(D, C)

out14.png

In ähnlicher Weise berechnen wir, wie sich die MIC ändert, wenn das Rauschen nach und nach erhöht wird.


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X + np.random.rand(51,) * d / 10
    D.append(d)
    mine.compute_score(X, Y)
    C.append(mine.mic())

plt.plot(D, C)

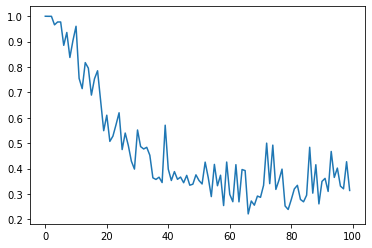
out15.png

In ähnlicher Weise berechnen wir, wie sich der HSIC ändert, wenn der Geräuschpegel nach und nach erhöht wird.

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X + np.random.rand(51,) * d / 10
    D.append(d)
    testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
    C.append(testStat / thresh)

plt.plot(D, C)

out16.png

quadratische Funktion

Als nächstes kommt die quadratische Funktion.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = X**2
plt.scatter(X, Y)

out17.png

Der Pearson-Korrelationskoeffizient ist

np.corrcoef(X, Y)[0, 1]

-2.3862043230836297e-17

MIC ist

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

9.285886928766184

Fügen wir Rauschen hinzu.

X = np.linspace(-1, 1, 51)
Y = X**2 + np.random.rand(51,)
plt.scatter(X, Y)

out21.png

Der Pearson-Korrelationskoeffizient ist

np.corrcoef(X, Y)[0, 1]

0.04693076570744622

MIC ist

mine.compute_score(X, Y)
mine.mic()

0.5071787519579662

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

5.247036645612692

Berechnen wir, wie sich der Pearson-Korrelationskoeffizient ändert, wenn das Rauschen nach und nach zunimmt.


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X**2 + np.random.rand(51,) * d / 10
    D.append(d)
    C.append(np.corrcoef(X, Y)[0, 1])

plt.plot(D, C)

out25.png

In ähnlicher Weise berechnen wir, wie sich die MIC ändert, wenn das Rauschen nach und nach erhöht wird.


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X**2 + np.random.rand(51,) * d / 10
    D.append(d)
    mine.compute_score(X, Y)
    C.append(mine.mic())

plt.plot(D, C)

out26.png

In ähnlicher Weise berechnen wir, wie sich der HSIC ändert, wenn der Geräuschpegel nach und nach erhöht wird.

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X**2 + np.random.rand(51,) * d / 10
    D.append(d)
    testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
    C.append(testStat / thresh)

plt.plot(D, C)

out27.png

Es ist ersichtlich, dass der Pearson-Korrelationskoeffizient die Beziehung der quadratischen Funktion nicht erfassen konnte, während sowohl MIC als auch HSIC erfasst werden konnten. Sie können auch sehen, dass das MIC von kleinen Geräuschen weitgehend unberührt bleibt.

Trigonometrische Funktion

Schauen wir uns auch die Dreiecksfunktion an.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = np.sin((X)*np.pi*2)
plt.scatter(X, Y)

out39.png

Der Pearson-Korrelationskoeffizient ist

np.corrcoef(X, Y)[0, 1]

-0.37651692742033543

MIC ist

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

3.212604441715373

Fügen wir Rauschen hinzu.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = np.sin((X+0.25)*np.pi*2) + np.random.rand(51,)
plt.scatter(X, Y)

out43.png

Der Pearson-Korrelationskoeffizient ist

np.corrcoef(X, Y)[0, 1]

0.049378342546505014

MIC ist

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

1.3135420547013614

Untersuchen Sie den Effekt der Erhöhung des Rauschens. Der Pearson-Korrelationskoeffizient ist

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = np.sin((X+0.25)*np.pi*2) + np.random.rand(51,) * d / 10
    D.append(d)
    C.append(np.corrcoef(X, Y)[0, 1])

plt.plot(D, C)

out47.png

MIC ist

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = np.sin((X+0.25)*np.pi*2) + np.random.rand(51,) * d / 10
    D.append(d)
    mine.compute_score(X, Y)
    C.append(mine.mic())

plt.plot(D, C)

out48.png

HSIC

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = np.sin((X+0.25)*np.pi*2) + np.random.rand(51,) * d / 10
    D.append(d)
    testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
    C.append(testStat / thresh)

plt.plot(D, C)

out49.png

Es wurde erwartet, dass der Pearson-Korrelationskoeffizient die Beziehung der Dreiecksfunktion zum Rauschen nicht erfassen konnte, aber es scheint, dass HSIC ebenfalls abgefallen ist. Unter ihnen war ich überrascht, dass MIC die Beziehung erkennen konnte.

Sigmaid-Funktion

Schließlich gibt es die Sigmoidfunktion.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = 1 / (1 + np.exp(-X*10))
plt.scatter(X, Y)

out58.png

Der Pearson-Korrelationskoeffizient ist

np.corrcoef(X, Y)[0, 1]

0.9354020629807919

MIC ist

mine.compute_score(X, Y)
mine.mic()

0.9999999999999998

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

27.433932271008874

Fügen wir Rauschen hinzu.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = 1 / (1 + np.exp(-X*10)) + np.random.rand(51,)
plt.scatter(X, Y)

out62.png

Der Pearson-Korrelationskoeffizient ist

np.corrcoef(X, Y)[0, 1]

0.7994507640548881

MIC ist

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

12.218008194240534

Lassen Sie uns sehen, wie sich das Rauschen erhöht. Der Pearson-Korrelationskoeffizient ist


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = 1 / (1 + np.exp(-X*10)) + np.random.rand(51,) * d / 10
    D.append(d)
    C.append(np.corrcoef(X, Y)[0, 1])

plt.plot(D, C)

out66.png

MIC ist

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = 1 / (1 + np.exp(-X*10)) + np.random.rand(51,) * d / 10
    D.append(d)
    mine.compute_score(X, Y)
    C.append(mine.mic())

plt.plot(D, C)

out67.png

HSIC


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = 1 / (1 + np.exp(-X*10)) + np.random.rand(51,) * d / 10
    D.append(d)
    testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
    C.append(testStat / thresh)

plt.plot(D, C)

out68.png

Alle Indikatoren können die Beziehung erkennen, aber in Bezug auf die Rauschbeständigkeit scheint MIC am stärksten zu sein.

Es ist ein individueller Eindruck

MIC MIC!

Recommended Posts

Korrelationskoeffizient MIC, der nichtlineare Beziehungen verarbeiten kann, und Hilbert-Schmidt-Unabhängigkeitstest HSIC