Das Deep Learning-Framework Chainer, das ein heißes Thema ist, enthält Beispielcode zur Unterscheidung handgeschriebener Zeichen. Ich möchte einen Artikel schreiben, der den Inhalt ein wenig erklärt.

** (Der vollständige Code für diesen Artikel wurde auf [GitHub] hochgeladen (https://github.com/matsuken92/Qiita_Contents/blob/master/chainer-MNIST/chainer-MNIST_forPubs.ipynb) [PC empfohlen]) ** ** **

Wie auch immer, es ist sehr einfach zu installieren und wenn Sie Python schreiben, können Sie es sofort verwenden, also empfehle ich es! Es ist großartig, Code in Python schreiben zu können.

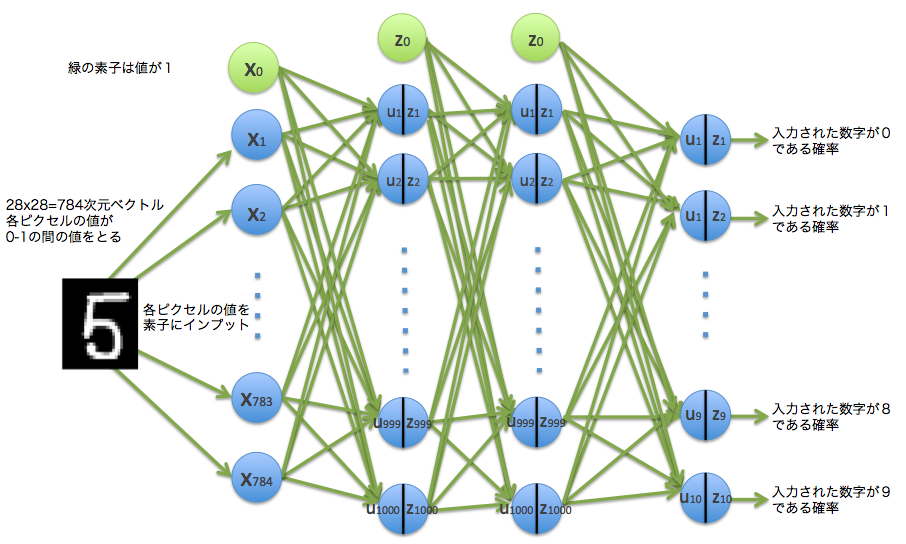
Es ist ein Artikel, um ein neuronales Netzwerkmodell wie dieses auszuprobieren.

Die wichtigsten Informationen finden Sie hier. Chainers Hauptseite GitHub-Repository von Chainer Chainer-Tutorials und Referenzen

1. Installationsnummer

Zunächst ist es eine Installation. Lesen Sie nach der Installation der erforderlichen Software und Bibliotheken unter "Anforderungen" (https://github.com/pfnet/chainer#requirements) auf GitHub of Chainer nach.

pip install chainer

Ausführen. Sie können es mit genau diesem installieren. Super einfach! Ich hatte einige Probleme, als ich versuchte, Caffe auf meinem Mac zu installieren, aber es scheint eine Lüge zu sein: Lächeln:

Wenn Sie in der Installation nicht weiterkommen, wird der Artikel "Chainer of Deep Learning-Bibliothek von cvl-robot scheint erstaunlich zu sein" ausführlich beschrieben. Dies ist praktisch, da hier die Installation der erforderlichen Bibliotheken beschrieben wird.

2. Holen Sie sich den Beispielcode

Im folgenden Verzeichnis von GitHub befindet sich ein Beispiel, das die bekannten handgeschriebenen MNIST-Zeichen unterscheidet. Daher möchte ich dies als Betreff verwenden. Dies ist ein Versuch, dies mit dem vorwärtsgerichteten neuronalen Netzwerk von Chainer zu klassifizieren. https://github.com/pfnet/chainer/tree/master/examples/mnist 　　┗ train_mnist.py

Ich möchte diesem Code einen Kommentar hinzufügen und einen Teil des Flusses in einem Diagramm anzeigen, um ein Bild hinzuzufügen.

3. Sehen Sie sich den Beispielcode # an

Dieses Mal schreibe ich, während ich den Betrieb auf meinem Macbook Air (OS X Version 10.10.2) überprüfe, sodass es je nach Umgebung Unterschiede geben kann, aber ich hoffe, dass Sie es sehen können. Aufgrund dieser Umgebung wird der GPU-bezogene Code weggelassen, da nur die CPU ohne Berechnung auf der GPU verwendet wird.

3-1. Vorbereitung

Der erste ist der Import der erforderlichen Bibliotheken.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_mldata
from chainer import cuda, Variable, FunctionSet, optimizers
import chainer.functions  as F
import sys

plt.style.use('ggplot')

Definieren und stellen Sie als Nächstes verschiedene Parameter ein.

#Chargengröße für eine Charge beim Training mit der probabilistischen Gradientenabstiegsmethode
batchsize = 100

#Anzahl der Wiederholungen des Lernens
n_epoch   = 20

#Anzahl der mittleren Schichten
n_units   = 1000

Verwenden Sie Scikit Learn, um handgeschriebene numerische MNIST-Daten herunterzuladen.

#Laden Sie handgeschriebene numerische MNIST-Daten herunter
# #HOME/scikit_learn_data/mldata/mnist-original.In Matte zwischengespeichert
print 'fetch MNIST dataset'
mnist = fetch_mldata('MNIST original')
# mnist.data : 70,000 784-dimensionale Vektordaten
mnist.data   = mnist.data.astype(np.float32)
mnist.data  /= 255     # 0-In 1 Daten konvertieren

# mnist.target :Richtige Antwortdaten (Lehrerdaten)
mnist.target = mnist.target.astype(np.int32)

Ich werde ungefähr 3 herausnehmen und zeichnen.

#Funktion zum Zeichnen handgeschriebener numerischer Daten
def draw_digit(data):
    size = 28
    plt.figure(figsize=(2.5, 3))

    X, Y = np.meshgrid(range(size),range(size))
    Z = data.reshape(size,size)   # convert from vector to 28x28 matrix
    Z = Z[::-1,:]             # flip vertical
    plt.xlim(0,27)
    plt.ylim(0,27)
    plt.pcolor(X, Y, Z)
    plt.gray()
    plt.tick_params(labelbottom="off")
    plt.tick_params(labelleft="off")

    plt.show()

draw_digit(mnist.data[5])
draw_digit(mnist.data[12345])
draw_digit(mnist.data[33456])

Dies sind die Daten des 28x28.784-Dimensionsvektors.

Teilen Sie den Datensatz in Validierungsdaten für Trainingsdaten.

#Stellen Sie N Trainingsdaten und verbleibende Verifizierungsdaten ein
N = 60000
x_train, x_test = np.split(mnist.data,   [N])
y_train, y_test = np.split(mnist.target, [N])
N_test = y_test.size

3.2 Modelldefinition

Es ist endlich die Definition des Modells. Es ist die Produktion von hier. Verwenden Sie Chainer-Klassen und -Funktionen.

# Prepare multi-layer perceptron model
#Mehrschichtige Perceptron-Modelleinstellungen
#Geben Sie 784 Dimensionen ein, geben Sie 10 Dimensionen aus
model = FunctionSet(l1=F.Linear(784, n_units),
                    l2=F.Linear(n_units, n_units),
                    l3=F.Linear(n_units, 10))

Da die eingegebenen handgeschriebenen Zahlendaten ein 784-dimensionaler Vektor sind, gibt es 784 Eingabeelemente. Dieses Mal wird die mittlere Schicht in n_units als 1000 angegeben. Die Ausgabe ist 10, weil sie die Nummer identifiziert. Unten ist ein Bild dieses Modells.

Die Struktur der Vorwärtsausbreitung wird durch die folgende Funktion forward () definiert.

# Neural net architecture
#Neuronale Netzstruktur
def forward(x_data, y_data, train=True):
    x, t = Variable(x_data), Variable(y_data)
    h1 = F.dropout(F.relu(model.l1(x)),  train=train)
    h2 = F.dropout(F.relu(model.l2(h1)), train=train)
    y  = model.l3(h2)
    #Da es sich um eine Mehrklassenklassifizierung handelt, fungiert die Softmax-Funktion als Fehlerfunktion
    #Fehlerableitung mit Cross-Entropy-Funktion
    return F.softmax_cross_entropy(y, t), F.accuracy(y, t)

Ich möchte jede Funktion hier erklären. Bei der Chainer-Methode werden Daten von einem Array in ein Objekt vom Typ (Klasse) konvertiert und als Variable of Chainer bezeichnet und verwendet.

x, t = Variable(x_data), Variable(y_data)

Die Aktivierungsfunktion ist nicht die Sigmoidfunktion, sondern die Funktion F.relu ().

F.relu(model.l1(x))

Diese F.relu () ist eine Funktion der gleichgerichteten Lineareinheit

f(x) = \max(0, x)

Mit anderen Worten

Es ist so. Klicken Sie hier für den Zeichnungscode.

# F.relu test
x_data = np.linspace(-10, 10, 100, dtype=np.float32)
x = Variable(x_data)
y = F.relu(x)

plt.figure(figsize=(7,5))
plt.ylim(-2,10)
plt.plot(x.data, y.data)
plt.show()

Es ist eine einfache Funktion. Aus diesem Grund scheint der Vorteil darin zu liegen, dass der Rechenaufwand gering und die Lerngeschwindigkeit hoch ist.

Als nächstes wird die Funktion F.dropout () mit der Ausgabe dieser relu () -Funktion als Eingabe verwendet.

F.dropout(F.relu(model.l1(x)),  train=train)

Diese Dropout-Funktion F.dropout () wurde in dem Artikel Dropout: Ein einfacher Weg, um eine Überanpassung neuronaler Netze zu verhindern vorgeschlagen. Es scheint möglich zu sein, ein Überlernen zu verhindern, indem die mittlere Schicht (vorausgesetzt, sie existiert nicht) durch die Methode zufällig entfernt wird.

Bewegen wir es ein wenig.

# dropout(x, ratio=0.5, train=True)Prüfung
# x:Eingegebener Wert
# ratio:Wahrscheinlichkeit der Ausgabe von 0
# train:Wenn False, geben Sie x so wie es ist zurück
# return:0 mit einer Verhältniswahrscheinlichkeit, 1-Verhältniswahrscheinlichkeit,x*(1/(1-ratio))Gibt den Wert von zurück

n = 50
v_sum = 0
for i in range(n):
    x_data = np.array([1,2,3,4,5,6], dtype=np.float32)
    x = Variable(x_data)
    dr = F.dropout(x, ratio=0.6,train=True)
    
    for j in range(6):
        sys.stdout.write( str(dr.data[j]) + ', ' )
    print("")
    v_sum += dr.data

#Der Durchschnitt der Ausgabe ist x_Entspricht ungefähr den Daten
sys.stdout.write( str((v_sum/float(n))) )

`output`


2.5, 5.0, 7.5, 0.0, 0.0, 0.0, 
2.5, 5.0, 7.5, 10.0, 0.0, 15.0, 
0.0, 5.0, 7.5, 10.0, 12.5, 15.0, 
・ ・ ・
0.0, 0.0, 7.5, 10.0, 0.0, 0.0, 
2.5, 0.0, 7.5, 10.0, 0.0, 15.0, 
[ 0.94999999  2.29999995  3.          3.5999999   7.25        5.69999981]

Übergeben Sie das Array [1,2,3,4,5,6] an die Funktion F.dropout (). Das Verhältnis ist nun die Abbrecherquote, und da das Verhältnis = 0,6 festgelegt ist, besteht eine Wahrscheinlichkeit von 60%, dass es abgebrochen wird und 0 ausgegeben wird. Der Wert wird mit einer Wahrscheinlichkeit von 40% zurückgegeben, aber zu diesem Zeitpunkt wurde die Wahrscheinlichkeit, den Wert zurückzugeben, auf 40% reduziert. Um dies auszugleichen, ist $ {1 \ über 0,4} $ mal = 2,5 mal Der Wert wird ausgegeben. Mit anderen Worten

(0 \times 0.6 + 2.5 \times 0.4) = 1

Im Durchschnitt ist es also die ursprüngliche Nummer. Im obigen Beispiel ist die letzte Zeile der Durchschnitt der Ausgabe, wird jedoch 50 Mal wiederholt und der Wert liegt nahe am Original [1,2,3,4,5,6].

Es gibt eine weitere Schicht derselben Struktur, und der Ausgabewert ist $ y $.

    h2 = F.dropout(F.relu(model.l2(h1)), train=train)
    y  = model.l3(h2)

Die endgültige Ausgabe ist die Fehlerausgabe unter Verwendung der Softmax-Funktion und der Kreuzentropiefunktion. Und die Funktion F.accuracy () gibt die Genauigkeit zurück.

    #Da es sich um eine Mehrklassenklassifizierung handelt, fungiert die Softmax-Funktion als Fehlerfunktion
    #Fehlerableitung mit Cross-Entropy-Funktion
    return F.softmax_cross_entropy(y, t), F.accuracy(y, t)

Obwohl es sich um eine Softmax-Funktion handelt,

y_k = z_k = f_{k}({\bf u})={\exp(u_{k}) \over \sum_j^K \exp(u_{j})}

Durch Sandwiching dieser Funktion mit einer Funktion, die definiert ist als, wird die Summe von 10 Ausgaben von $ y_1, \ cdots, y_ {10} $ zu 1, und die Ausgaben können als Wahrscheinlichkeiten interpretiert werden. Ich verstehe, dass der Grund, warum die Funktion $ \ exp () $ verwendet wird, darin besteht, dass der Wert nicht negativ sein sollte.

Die bekannte $ \ exp () $ -Funktion ist exp-compressor (1).png Da es eine ähnliche Form hat, nimmt es keinen negativen Wert an. Infolgedessen wird der Wert nicht negativ und die Summe ist 1, was als Wahrscheinlichkeit interpretiert werden kann. Unter Verwendung des Ausgabewerts $ y_k $ der Softmax-Funktion wird die Kreuzentropiefunktion verwendet

E({\bf w}) = -\sum_{n=1}^{N} \sum_{k=1}^{K} t_{nk} \log y_k ({\bf x}_n, {\bf w})

Es wird ausgedrückt als.

Im Chainer-Code https://github.com/pfnet/chainer/blob/master/chainer/functions/softmax_cross_entropy.py Es ist in,

def forward_cpu(self, inputs):
        x, t = inputs
        self.y, = Softmax().forward_cpu((x,))
        return -numpy.log(self.y[xrange(len(t)), t]).sum(keepdims=True) / t.size,

Entspricht.

Außerdem stimmt "Genauigkeit (y, t)" die Ausgabe mit den Lehrerdaten ab und gibt die richtige Antwortrate zurück.

3.3 Optimierungseinstellungen

Nachdem das Modell festgelegt wurde, können wir mit dem Training fortfahren. Adam wird hier als Optimierungsmethode verwendet.

# Setup optimizer
optimizer = optimizers.Adam()
optimizer.setup(model.collect_parameters())

Echizen_tm erklärt Adam in Adam in 30 Minuten. Ich bin.

4. Durchführung des Trainings und Ergebnisse

Aus den obigen Vorbereitungen werden wir handschriftliche Zahlen durch Mini-Batch-Lernen unterscheiden und die Genauigkeit überprüfen.

train_loss = []
train_acc  = []
test_loss = []
test_acc  = []

l1_W = []
l2_W = []
l3_W = []

# Learning loop
for epoch in xrange(1, n_epoch+1):
    print 'epoch', epoch

    # training
    #Sortieren Sie die Reihenfolge von N Teilen nach dem Zufallsprinzip
    perm = np.random.permutation(N)
    sum_accuracy = 0
    sum_loss = 0
    #Lernen mit Daten von 0 bis N für jede Chargengröße
    for i in xrange(0, N, batchsize):
        x_batch = x_train[perm[i:i+batchsize]]
        y_batch = y_train[perm[i:i+batchsize]]

        #Initialisieren Sie den Farbverlauf
        optimizer.zero_grads()
        #Berechnen Sie Fehler und Genauigkeit durch Vorwärtsausbreitung
        loss, acc = forward(x_batch, y_batch)
        #Berechnen Sie den Gradienten durch Fehlerrückausbreitung
        loss.backward()
        optimizer.update()

        train_loss.append(loss.data)
        train_acc.append(acc.data)
        sum_loss     += float(cuda.to_cpu(loss.data)) * batchsize
        sum_accuracy += float(cuda.to_cpu(acc.data)) * batchsize

    #Zeigen Sie Trainingsdatenfehler und korrekte Antwortgenauigkeit an
    print 'train mean loss={}, accuracy={}'.format(sum_loss / N, sum_accuracy / N)

    # evaluation
    #Berechnen Sie den Fehler und die korrekte Antwortgenauigkeit aus den Testdaten und überprüfen Sie die Generalisierungsleistung
    sum_accuracy = 0
    sum_loss     = 0
    for i in xrange(0, N_test, batchsize):
        x_batch = x_test[i:i+batchsize]
        y_batch = y_test[i:i+batchsize]

        #Berechnen Sie Fehler und Genauigkeit durch Vorwärtsausbreitung
        loss, acc = forward(x_batch, y_batch, train=False)

        test_loss.append(loss.data)
        test_acc.append(acc.data)
        sum_loss     += float(cuda.to_cpu(loss.data)) * batchsize
        sum_accuracy += float(cuda.to_cpu(acc.data)) * batchsize

    #Anzeigefehler in den Testdaten und korrekte Antwortgenauigkeit
    print 'test  mean loss={}, accuracy={}'.format(sum_loss / N_test, sum_accuracy / N_test)

    #Speichern Sie gelernte Parameter
    l1_W.append(model.l1.W)
    l2_W.append(model.l2.W)
    l3_W.append(model.l3.W)

#Genauigkeit und Fehler beim Zeichnen von Diagrammen
plt.figure(figsize=(8,6))
plt.plot(range(len(train_acc)), train_acc)
plt.plot(range(len(test_acc)), test_acc)
plt.legend(["train_acc","test_acc"],loc=4)
plt.title("Accuracy of digit recognition.")
plt.plot()

Hier ist das zusammenfassende Ergebnis für jede Epoche. Es kann mit einer hohen Genauigkeit von etwa 98,5% durch 20-maliges Drehen unterschieden werden.

`output`


epoch 1
train mean loss=0.278375425202, accuracy=0.914966667456
test  mean loss=0.11533634907, accuracy=0.964300005436
epoch 2
train mean loss=0.137060894324, accuracy=0.958216670454
test  mean loss=0.0765812527167, accuracy=0.976100009084
epoch 3
train mean loss=0.107826075749, accuracy=0.966816672881
test  mean loss=0.0749603212342, accuracy=0.97770000577
epoch 4
train mean loss=0.0939164237926, accuracy=0.970616674324
test  mean loss=0.0672153823725, accuracy=0.980000005364
epoch 5
train mean loss=0.0831089563683, accuracy=0.973950009048
test  mean loss=0.0705943618687, accuracy=0.980100004673
epoch 6
train mean loss=0.0752325405277, accuracy=0.976883343955
test  mean loss=0.0732760328815, accuracy=0.977900006771
epoch 7
train mean loss=0.0719517664274, accuracy=0.977383343875
test  mean loss=0.063611669606, accuracy=0.981900005937
epoch 8
train mean loss=0.0683009948514, accuracy=0.978566677173
test  mean loss=0.0604036964733, accuracy=0.981400005221
epoch 9
train mean loss=0.0621755663728, accuracy=0.980550010701
test  mean loss=0.0591542539285, accuracy=0.982400006652
epoch 10
train mean loss=0.0618313539471, accuracy=0.981183344225
test  mean loss=0.0693172766063, accuracy=0.982900006175
epoch 11
train mean loss=0.0583098273944, accuracy=0.982000010014
test  mean loss=0.0668152360269, accuracy=0.981600006819
epoch 12
train mean loss=0.054178619228, accuracy=0.983533344865
test  mean loss=0.0614466062452, accuracy=0.982900005579
epoch 13
train mean loss=0.0532431817259, accuracy=0.98390001148
test  mean loss=0.060112986485, accuracy=0.98400000751
epoch 14
train mean loss=0.0538122716064, accuracy=0.983266676267
test  mean loss=0.0624165921964, accuracy=0.983300005198
epoch 15
train mean loss=0.0501562882114, accuracy=0.983833344777
test  mean loss=0.0688113694015, accuracy=0.98310000658
epoch 16
train mean loss=0.0513108611095, accuracy=0.984533343514
test  mean loss=0.0724038232205, accuracy=0.982200007439
epoch 17
train mean loss=0.0471463404785, accuracy=0.985666677058
test  mean loss=0.0612579581685, accuracy=0.983600008488
epoch 18
train mean loss=0.0460166006556, accuracy=0.986050010125
test  mean loss=0.0654888718335, accuracy=0.984400007725
epoch 19
train mean loss=0.0458772557077, accuracy=0.986433342795
test  mean loss=0.0602016936944, accuracy=0.984400007129
epoch 20
train mean loss=0.046333729005, accuracy=0.986433343093
test  mean loss=0.0621869922416, accuracy=0.985100006461

Hier ist ein Diagramm der Unterscheidungsgenauigkeit und des Fehlers für jede Charge. Das rote sind die Trainingsdaten und das blaue sind die Testdaten.

Zuvor wurde ein Artikel [Maschinelles Lernen] k-Nearest-Neighbour-Methode (k-Nearest-Neighbour-Methode) von sich selbst in Python geschrieben und erkennt handgeschriebene Zahlen Also habe ich auch versucht, handschriftliche Zahlen zu unterscheiden, aber die Genauigkeit lag zu diesem Zeitpunkt bei etwa 97%, sodass ich sehen kann, dass sie sich etwas weiter verbessert hat.

Dieser Chiner kann vollständig mit Python-Code betrieben werden, daher denke ich, dass er ein sehr schönes Framework für Pythonista ist. Ich habe noch nicht "tief" gelernt, es ist nur ein Feedforward-neuronales Netzwerk, daher möchte ich in naher Zukunft einen Artikel über "tief" schreiben.

5. Übereinstimmende Antworten

Lassen Sie uns die 100 identifizierten Nummern anzeigen. Ich habe 100 zufällig extrahiert, aber die Antwort ist fast richtig. Nachdem ich 100 Elemente mehrmals angezeigt hatte, konnte ich endlich ein falsches Teil anzeigen. Ein Beispiel ist unten dargestellt. Es fühlt sich an, als würden Menschen getestet (lacht)

(* 4 in 2 Zeilen und 3 Spalten wird fälschlicherweise als 9 identifiziert)

plt.style.use('fivethirtyeight')
def draw_digit3(data, n, ans, recog):
    size = 28
    plt.subplot(10, 10, n)
    Z = data.reshape(size,size)   # convert from vector to 28x28 matrix
    Z = Z[::-1,:]             # flip vertical
    plt.xlim(0,27)
    plt.ylim(0,27)
    plt.pcolor(Z)
    plt.title("ans=%d, recog=%d"%(ans,recog), size=8)
    plt.gray()
    plt.tick_params(labelbottom="off")
    plt.tick_params(labelleft="off")
    

plt.figure(figsize=(15,15))

cnt = 0
for idx in np.random.permutation(N)[:100]:
    
    xxx = x_train[idx].astype(np.float32)
    h1 = F.dropout(F.relu(model.l1(Variable(xxx.reshape(1,784)))),  train=False)
    h2 = F.dropout(F.relu(model.l2(h1)), train=False)
    y  = model.l3(h2)
    cnt+=1
    draw_digit3(x_train[idx], cnt, y_train[idx], np.argmax(y.data))
plt.show

6. Visualisierung des Parameters w der ersten Schicht

Eingabeebenenparameter $ w ^ {(1)} $ 784 Ich habe einen dreidimensionalen Vektor als 28x28 Pixel abgebildet und angezeigt. 100 von 1000 werden zufällig ausgewählt. Wenn Sie genau hinschauen, gibt es einige, die wie "2", "5" oder "0" aussehen. Sie können die Atmosphäre sehen, in der die Features mit den Parametern der ersten Ebene extrahiert werden können.

def draw_digit2(data, n, i):
    size = 28
    plt.subplot(10, 10, n)
    Z = data.reshape(size,size)   # convert from vector to 28x28 matrix
    Z = Z[::-1,:]             # flip vertical
    plt.xlim(0,27)
    plt.ylim(0,27)
    plt.pcolor(Z)
    plt.title("%d"%i, size=9)
    plt.gray()
    plt.tick_params(labelbottom="off")
    plt.tick_params(labelleft="off")

plt.figure(figsize=(10,10))
cnt = 1
for i in np.random.permutation(1000)[:100]:
    draw_digit2(l1_W[len(l1_W)-1][i], cnt, i)
    cnt += 1
    
plt.show()

7. Visualisierung des Ausgabeschichtparameters w

Die Ausgabeebene ist eine Ebene, die 1000 Eingaben empfängt und 10 Ausgaben ausgibt, aber ich habe auch versucht, sie zu visualisieren. Die Stelle, an der "0" geschrieben wird, ist der Parameter, um die handschriftliche Nummer als "0" zu unterscheiden.

Da es sich um einen 1000-dimensionalen Vektor handelt, werden am Ende 24 0s hinzugefügt, um ein 32x32-Bild zu erstellen.

#Schicht 3
def draw_digit2(data, n, i):
    size = 32
    plt.subplot(4, 4, n)
    data = np.r_[data,np.zeros(24)]
    Z = data.reshape(size,size)   # convert from vector to 28x28 matrix
    Z = Z[::-1,:]             # flip vertical
    plt.xlim(0,size-1)
    plt.ylim(0,size-1)
    plt.pcolor(Z)
    plt.title("%d"%i, size=9)
    plt.gray()
    plt.tick_params(labelbottom="off")
    plt.tick_params(labelleft="off")

plt.figure(figsize=(10,10))
cnt = 1
for i in range(10):
    draw_digit2(l3_W[len(l3_W)-1][i], cnt, i)
    cnt += 1
    
plt.show()

8. Bonus

Die Anzahl der Elemente in der Zwischenschicht wurde auf "[100, 500, 800, 900, 1000, 1100, 1200, 1500, 2000]" eingestellt und jedes wurde unterschieden. Das resultierende Diagramm ist unten. Mit mehr als 500 Elementen haben wir ungefähr 98% erreicht, und es scheint, dass sich die Anzahl der darüber hinausgehenden Elemente nicht wesentlich ändert.

9. Bonus 2: Aktivierungsfunktion

Für die in Chainer vorinstallierten Hauptaktivierungsfunktionen

ReLu function
tanh function
sigmoid function

es gibt. Es sieht aus wie in der Abbildung unten. Es ist eine Funktion, die zwischen Eingabe und Ausgabe des Elements wechselt und die Aufgabe hat, einen Schwellenwert für Eingabe und Ausgabe festzulegen.

#Aktivierungsfunktionstest
x_data = np.linspace(-10, 10, 100, dtype=np.float32)
x = Variable(x_data)

y = F.relu(x)
plt.figure(figsize=(8,15))
plt.subplot(311)
plt.title("ReLu function.")
plt.ylim(-2,10)
plt.xlim(-6,6)
plt.plot(x.data, y.data)

y = F.tanh(x)
plt.subplot(312)
plt.title("tanh function.")
plt.ylim(-1.5,1.5)
plt.xlim(-6,6)
plt.plot(x.data, y.data)

y = F.sigmoid(x)
plt.subplot(313)
plt.title("sigmoid function.")
plt.ylim(-.2,1.2)
plt.xlim(-6,6)
plt.plot(x.data, y.data)
plt.show()

Nächster Artikel "[Deep Learning] Versuchen Sie Autoencoder mit Chainer, um die Ergebnisse zu visualisieren." Dies ist ein Artikel, der Autoencoder implementiert, eine Technologie, die die Merkmalsextraktion mit Deep Learning automatisiert.

[Nachschlagewerk] Deep Learning (professionelle Serie für maschinelles Lernen) Takayuki Okaya

[Referenzwebsite] Chainers Hauptwebsite 　　　http://chainer.org/ Chainers GitHub-Repository 　　　https://github.com/pfnet/chainer Chainer-Tutorials und Referenzen 　　　http://docs.chainer.org/en/latest/ 　"Dropout: A Simple Way to Prevent Neural Networks from Overfitting" 　 Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, Ruslan Salakhutdinov 　　　http://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf

[PYTHON] [Maschinelles Lernen] Ich werde es erklären, während ich das Deep Learning Framework Chainer ausprobiere.

1. Installationsnummer

2. Holen Sie sich den Beispielcode

3. Sehen Sie sich den Beispielcode # an

3-1. Vorbereitung

3.2 Modelldefinition

output

3.3 Optimierungseinstellungen

4. Durchführung des Trainings und Ergebnisse

output

5. Übereinstimmende Antworten

6. Visualisierung des Parameters w der ersten Schicht

7. Visualisierung des Ausgabeschichtparameters w

8. Bonus

9. Bonus 2: Aktivierungsfunktion

`output`

`output`