Obwohl theoretisch nicht gut verstanden, handelt es sich um eine Methode zur Schätzung der gekrümmten Oberfläche aus gestreuten Probenpunkten. Da es mit der in Latin Super-Square Sampling with OpenMDAO (Streustichprobe) gezeigten lateinischen Superquadrat-Stichprobe kompatibel ist, wird CAE technisch verwendet. Es wird häufig verwendet, um die Antwortfläche abzuschätzen.
Der Umriss der Bemühungen ist wie folgt. Lesen Sie zuerst die Daten (doe_paraboloid-Datei), die mit [Latin Super Square Sampling mit OpenMDAO] experimentiert wurden (http://qiita.com/TatsuyaKatayama/items/7bcf863bad444c6ad901). Als nächstes wird das Kriging-Näherungsmodell trainiert und unter Verwendung der gelesenen experimentellen Daten erstellt. Schließlich wird die Gültigkeit des Modells bestätigt, indem die Interpolationswerte des erstellten Kriging-Näherungsmodells als theoretische Lösung (Drahtrahmen) aufgetragen werden. Die folgende Gleichung ist die theoretische Lösung.
\begin{align}
& f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3 \\
{\rm subject \: to} \: \: \:& -50.0\leq x \leq 50.0 \\
& -50.0\leq y \leq 50.0
\end{align}
Bereiten Sie die folgende Datei training_mm.py vor
training_mm.py
from __future__ import print_function
from openmdao.api import Group, MetaModel, FloatKrigingSurrogate
class TrainingMM(Group):
''' FloatKriging gives responses as floats '''
def __init__(self):
super(TrainingMM, self).__init__()
# Create meta_model for f_x as the response
mm = self.add("parabo_mm", MetaModel())
mm.add_param('x', val=0.)
mm.add_param('y', val=0.)
mm.add_output('f_xy', val=0., surrogate=FloatKrigingSurrogate())
Wir haben eine Komponente namens MetaModel hinzugefügt, die ein ungefähres Modell trainiert und dessen Wert bewertet. Ein Ersatzmodell namens FloatKrigingSurrogate wird auf ungefähr f_xy gesetzt. FloatKrigingSurrogate allein hat die Funktion, das ungefähre Modell zu trainieren und den Wert zu bewerten. Die offizielle Dokumentation besagt, dass MetaModel verwendet werden kann, um mehrere ungefähre Modelle gleichzeitig zu trainieren.
Bereiten Sie die folgende kriging_paraboloid.py vor. Die erste Hälfte ist der Prozess vom Lesen der experimentellen Daten bis zum Training des Kriging-Approximationsmodells.
kriging_paraboloid.py
#! /bin/python
import pickle
import numpy as np
import sqlitedict
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from openmdao.api import Problem
from training_mm import TrainingMM
db =sqlitedict.SqliteDict("doe_paraboloid","iterations")
res = np.array([[0.,0.,0.]] * len(db.items()))
for i, v in enumerate(db.items()):
res[i,0] = v[1]["Unknowns"]["x"]
res[i,1] = v[1]["Unknowns"]["y"]
res[i,2] = v[1]["Unknowns"]["f_xy"]
prob = Problem()
prob.root = TrainingMM()
prob.setup()
prob["parabo_mm.train:x"] = res[:,0]
prob["parabo_mm.train:y"] = res[:,1]
prob["parabo_mm.train:f_xy"] = res[:,2]
prob.run()
Die zweite Hälfte ist unten dargestellt. Ein Diagramm wird verwendet, um das erstellte Kriging-Approximationsmodell mit der theoretischen Lösung zu vergleichen.
kriging_paraboloid.py fuhr fort
x = np.arange(-50., 50., 4.)
y = np.arange(-50., 50., 4.)
sg = prob.root.parabo_mm._init_unknowns_dict["f_xy"]["surrogate"]
f = open("./kriging_parabo","w")
pickle.dump(sg, f)
f.close()
f = open("./kriging_parabo_mm","w")
pickle.dump(prob.root.parabo_mm, f)
f.close()
xyzkrig = np.array([[xi,yi,sg.predict(np.array([xi,yi]))[0]] \
for xi in x for yi in y])
#xyzkrig = np.array([[0.,0.,0.]]*(25*25))
#cnt = 0
#for xi in x:
# for yi in y:
# xyzkrig[cnt,0] = prob["parabo_mm.x"] = xi
# xyzkrig[cnt,1] = prob["parabo_mm.y"] = yi
# prob.run()
# xyzkrig[cnt,2] = prob["parabo_mm.f_xy"]
# cnt += 1
fig = plt.figure(figsize=(6,4)); ax = Axes3D(fig)
X, Y = np.meshgrid(x, y)
Z = (X-3.0)**2. + X*Y + (Y+4.0)**2. - 3.0
ax.plot_wireframe(X,Y,Z,label="theoretical surface")
ax.scatter3D(xyzkrig[:,0], xyzkrig[:,1], xyzkrig[:,2], c="r", marker="o",label="Interpolated value")
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('f_xy')
plt.legend()
plt.show()
Die erste Hälfte von kriging_paraboloid.py wird weggelassen und nur die zweite Hälfte wird erklärt. Zunächst haben wir Stichprobenpunkte erstellt, um das Kriging-Näherungsmodell zu bewerten. Dies unterscheidet sich vom Punkt der LHS (Latin Super Square Sampling). Der Bereich von $ -50 \ leq x, y \ leq 50 $ wird durch 25 x 25 Abtastpunkte bewertet, die in 25 unterteilt sind.
sg = prob.root.parabo_mm._init_unknowns_dict["f_xy"]["surrogate"]Mit privaten Klassenvariablen(_init_unknowns_dict)Zugreifen,Laden des in Meata Model installierten Ersatzmodells.
Es ist kein Kompliment, aber dafür gibt es zwei Gründe.
* Das Speichern eines trainierten Approximationsmodells ist nicht implementiert. Dieses Mal wurde es mit pickele serialisiert.
* Wenn Sie versuchen, den Wert eines ungefähren Modells mit MetaModel zu bewerten, wird dies etwas kompliziert (`` `# xyzkrig = ・ ・ ・` `` unter der Kommentarzeile).
Der Rest plant.
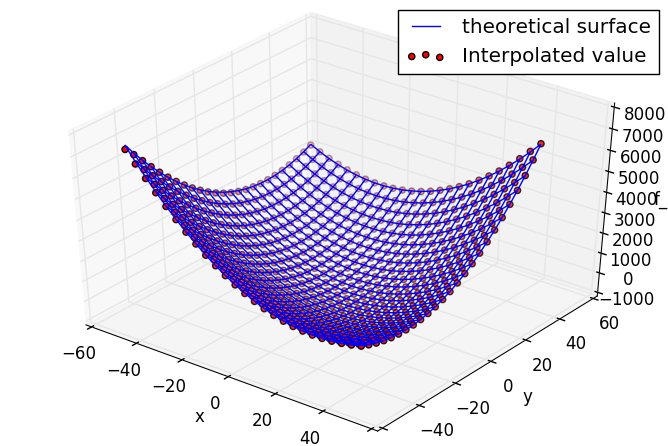
Die theoretische Lösung ist auf einem Drahtrahmen mit Punkten der Bewertungswerte des Kriging-Näherungsmodells aufgetragen.
# Interpolation von Werten durch das Kriging-Näherungsmodell
Die Genauigkeit scheint ziemlich gut zu sein, da die Anzahl der LHS-Proben zu groß war.
---