[PYTHON] Miyashitas Beispiel für analytische Mechanik löste Übungen und bewegte sich mit Animation

Miyashita Ich löse Übungen in analytischer Mechanik. Wenn Sie Fehler finden, lassen Sie es uns bitte wissen.

Kapitel 1

Für Pendelbewegungen der Länge $ l $ ist der Winkel $ \ phi $ die einzige inhaltliche Variable. Es ist bequemer, die Position des Versprechens in Polarkoordinaten anstelle von kartesischen Koordinaten auszudrücken. Durch die gute Verwendung von Variablen, die auf diese Weise Bindungsbedingungen berücksichtigen, ist es möglich, wesentliche Bewegungsvariablen zu handhaben.

Finden Sie den Lagrange des Pendels (Abb. 1.3) in orthogonalen Koordinaten (x, y). (Beispiel in Kapitel 2, S. 11)

Die kinetische Energie beträgt $ T = 1 / 2m \ dot {x} ^ 2 + 1 / 2m \ dot {y} ^ 2 $, und die potentielle Energie beträgt $ U = mgy $ Deshalb Lagrange $L=\frac{m}{2}(\dot{x}^2+\dot{y}^2)-mgy$ Auch hier sind die Bindungsbedingungen x^2+y^2=l^2 Es gibt.

Finden Sie den Lagrange des Pendels (Abb. 1.3) in Polarkoordinaten (l, Φ). (Beispiel in Kapitel 2, S. 12)

x=l\sin \phi y=-l\cos \phi Als \dot{x}=\dot{l}\sin \phi + l\dot{\phi}\cos \phi \dot{y}=-\dot{l}\cos \phi + l\dot{\phi}\sin \phi Deshalb \frac{m}{2}(\dot{x}+\dot{y})^2=(\dot{l}\sin \phi + l\dot{\phi\}cos \phi)^2+(\dot{l}\sin \phi + l\dot{\phi}\cos \phi)^2=\frac{m}{2}(\dot{l}^2+l^2 \dot{\phi}^2) U=mgl\cos \phi Weil $ l $ konstant ist L=\frac{m}{2}(l^2 \dot{\phi}^2)+mgl\cos \phi Bindungsbedingungen können in Polarkoordinaten gut gehandhabt werden.

Bewegungsgleichung

Lagranges Bewegungsgleichung \frac{d}{dt}\frac{\partial L}{\partial \phi}=ml^2\ddot{\phi} \frac{\partial L}{\partial \phi}=-mgl\sin \phi \therefore \ddot{\phi}=-\frac{g}{l}\sin \phi

Bewegungsgleichung lösen

Finden Sie die Lösung der winzigen Vibration in der Nähe von Φ = 0.

Wenn Taylor zum ersten expandiert \dot{\phi}=\frac{p_φ}{ml^2} \dot{p_\phi}=mgl\phi Wird sein. Deshalb \ddot{\phi}=-\frac{g}{l}\phi Die allgemeine Lösung dieser Gleichung lautet \phi=A\cos(\sqrt{\frac{g}{l}}t+B) Wenn $ \ phi = \ phi_0 << 1, ist \ \ dot {\ phi} = 0 $ A=\phi_0, \ \dot{\phi}=A\frac{g}{l}\sin(B)=0 \therefore B=0 Deshalb, \phi=\phi_0 \cos(\sqrt{\frac{g}{l}}t)

Finden Sie die Schwingungslösung mit Φ0 als Anfangswert.

\ddot{\phi_1}=-\frac{g}{l}\sin(\phi_1) Hier $ \ phi_1 = \ phi + \ phi_0 $ Die Lösung dieser Gleichung kann leicht durch numerische Analyse von Python erhalten werden. Es ist notwendig, die Differentialgleichung zweiter Ordnung in die Differentialgleichung erster Ordnung zu ändern. \dot{\phi}=\omega \dot{\omega}=-\frac{g}{l}\sin \phi

Python verwendet scipy.integrate.solve_ivp. Dies ergibt das Integral der gewöhnlichen Differentialgleichung mit dem Anfangswert.

scipy.integrate.solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False, events=None, vectorized=False, args=None, **options) Im

Spaß: Funktion t_span: Integrationsbereich y0: Anfangswert Methode: 'RK45 explizite Runge-Tack-Methode t_eval: Zeit zum Speichern des Berechnungsergebnisses

Animation erstellen

Mikrovibration

%matplotlib inline 
from numpy import sin, cos
from scipy.integrate import solve_ivp
from matplotlib.animation import FuncAnimation
import matplotlib.pyplot as plt
import numpy as np

g = 9.8                                 #Schwerkraftbeschleunigung[m/s^2]
l = 1.0                                 #Pendellänge[m]


t_span = [0,20]                         #Beobachtungszeit[s]
dt = 0.05                               #Intervall[s]
t = np.arange(t_span[0], t_span[1], dt)           
phi_0 = 0.1                              #Anfangswinkel[deg]

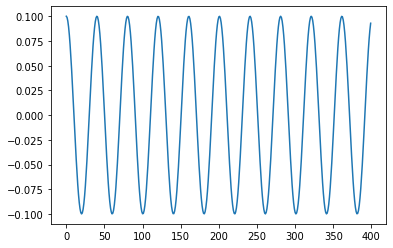
phi=phi_0*cos(np.sqrt(g/l)*t)
plt.plot(phi)

x = l * sin(phi)       
y = -l * cos(phi)      

fig, ax = plt.subplots()

line, = ax.plot([], [], 'o-', linewidth=2) 

def animation(i):
    thisx = [0, x[i]]
    thisy = [0, y[i]]

    line.set_data(thisx, thisy)
    return line,

ani = FuncAnimation(fig, animation, frames=np.arange(0, len(t)), interval=25, blit=True)

ax.set_xlim(-l,l)
ax.set_ylim(-l,l)
ax.set_aspect('equal')
ax.grid()
ani.save('pendulum.gif', writer='pillow', fps=15)
plt.show()

Vibration

g = 10                                 #Schwerkraftbeschleunigung[m/s^2]
l = 1                                 #Pendellänge[m]

def models(t, state):#Bewegungsgleichung
    dy = np.zeros_like(state)
    dy[0] = state[1]
    dy[1] = -(g/l)*sin(state[0])
    return dy

t_span = [0,20]                         #Beobachtungszeit[s]
dt = 0.05                               #Intervall[s]
t = np.arange(t_span[0], t_span[1], dt)
phi_0 = 90.0                              #Anfangswinkel[deg]
omega_0 = 0.0                                #Anfangswinkelgeschwindigkeit[deg/s]

state = np.radians([phi_0, omega_0])           #Ausgangszustand

results = solve_ivp(models, t_span, state, t_eval=t)
phi = results.y[0,:]

plt.plot(phi)

x = l * sin(phi)       
y = -l * cos(phi)      

fig, ax = plt.subplots()

line, = ax.plot([], [], 'o-', linewidth=2) #Zeichnen Sie, indem Sie dieser Linie nacheinander Koordinaten zuweisen

def animation(i):
    thisx = [0, x[i]]
    thisy = [0, y[i]]

    line.set_data(thisx, thisy)
    return line,

ani = FuncAnimation(fig, animation, frames=np.arange(0, len(t)), interval=25, blit=True)

ax.set_xlim(-l,l)
ax.set_ylim(-l,l)
ax.set_aspect('equal')
ax.grid()
plt.show()

ani.save('pendulum.gif', writer='pillow', fps=15)

Kapitel 2

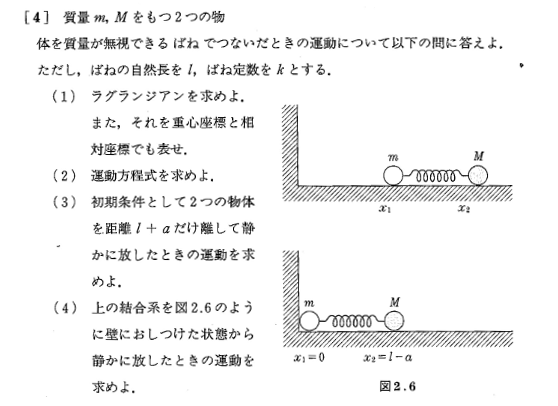
Unter der Annahme, dass die Koordinaten der Verpfändungspunkte ($ x_1, y_1 ) bzw. ( x_2, y_2 $) sind, ist die kinetische Energie dieses Systems

T=\frac{m_1}{2}(\dot{x_1}^2+\dot{y_1}^2)+\frac{m_2}{2}(\dot{x_2}^2+\dot{y_2}^2) Die Energie der Position U=m_1gy_1+m_2gy_2 Auch die Bindungsbedingungen sind x_1^2+y_1^2=l_1^2, (x_2-x_1)^2+(y_2-y_1)^2=l_2^2 Ist. Es ist notwendig, Lagranges unentschlossene Konstante zu verwenden, um die kinetische Gleichung für Lagrange zu lösen. Daher werden wir auch in diesem Fall Polarkoordinaten verwenden.

x_1=l_1\sin \theta_1 y_1=l_1\cos \theta_1 x_2=l_1\sin \theta_1+l_2\sin \theta_2 y_2=l_1\cos \theta_1+l_2\cos \theta_2

Da $ l_1 und \ l_2 $ konstant sind, ist jedes zeitdifferenziert. \dot{x_1}=l_1\dot{\theta_1}\cos \theta_1 \dot{y_1}=-l_1\dot{\theta_1}\sin \theta_1 \dot{x_2}=l_1\dot{\theta_1}\cos \theta_1+l_2\dot{\theta_2}\cos \theta_2 \dot{y_2}=-l_1\dot{\theta_1}\sin \theta_1-l_2\dot{\theta_2}\sin \theta_2 Übungsenergie T_1=\frac{m_1}{2}l_1^2\dot{\theta_1}^2(\sin^2\theta_1+\cos^2\\theta_1)=\frac{m_1}{2}l_1^2\dot{\theta_1}^2 T_2=\frac{m_2}{2}[(l_1\dot{\theta_1}\sin\theta_1 +l_2\dot{\theta_2}\sin\theta_2 )^2+(-l_1\dot{\theta_1}\cos\theta_1-l_2\dot{\theta_2}\cos\theta_2 )^2] \ =\frac{m_2}{2}(l_1^2\dot{\theta_1}^2\sin^2\theta_1+2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin\theta_1\sin\theta_2+l_1^2\dot{\theta_2}^2\sin^2\theta_2+l_1^2\dot{\theta_1}^2\cos^2\theta_1+2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos\theta_1\cos\theta_2+l_1^2\dot{\theta_2}\cos^2\theta_2) \ =\frac{m_2}{2} (l_1^2\dot{\theta_1}^2+2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)+l_1^2\dot{\theta_2}^2) T=T_1+T_2=\frac{m_1+m_2}{2}l_1^2\dot{\theta_1}^2+\frac{m_2}{2}(2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)+l_1^2\dot{\theta_2}^2) Die Energie der Position U_1=-m_1gl_1\cos\theta_1 U_2=-m_2g(l_1\cos\theta_1+l_2\cos\theta_2) U=U_1+U_2=-(m_1+m_2)gl_1\cos\theta_1-m_2gl_2\cos\theta_2 Deshalb Lagrange L=T-U=\frac{m_1+m_2}{2}l_1^2\dot{\theta_1}^2+\frac{m_2}{2}(2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)+l_2^2\dot{\theta_2}^2)+(m_1+m_2)gl_1\cos\theta_1+m_2gl_2\cos\theta_2

Um die Bewegungsgleichung von Euler Lagrangian zu finden \frac{\partial L}{\partial \theta_1}=-m_2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin(\theta_1-\theta_2)+(m_1+m_2)gl_1\sin\theta_1

\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_1}}=\frac{d}{dt}[(m_1+m_2)l_1^2\dot{\theta_1}+m_2l_1l_2\dot{\theta_2}\cos(\theta_1-\theta_2)] \ = (m_1+m_2)l_1^2\ddot{\theta_1}+m_2l_1l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)

\frac{\partial L}{\partial \theta_2}=m_2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin(\theta_1-\theta_2)-m_2gl_2\sin\theta_2 \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_2}}=\frac{d}{dt}[m_2l_1l_2\dot{\theta_1}\cos(\theta_1-\theta_2)+m_2l_2^2\dot{\theta_2})] \ = m_2l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2)+m_2l_2^2\ddot{\theta_2}

\therefore m_2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin(\theta_1-\theta_2)-(m_1+m_2)gl_1\sin\theta_1 = (m_1+m_2)l_1^2\ddot{\theta_1}+m_2l_1l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)

m_2l_1l_2\dot{\theta_1}\dot{\theta_2}\sin(\theta_1-\theta_2)-m_2gl_2\sin\theta_2= m_2l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2)-m_2l_2^2\ddot{\theta_2}

Übungen S.20-21

(1) Da die auf das Objekt A ausgeübte Kraft $ (kx) $ ist, ist die Positionsenergie $ U = -kx ^ 2 $, die kinetische Energie $ T = \ frac {1} {2} m \ dot {x} ^ 2 $ Auf das Objekt B $ kmg $, $ U = Mgx $, kinetische Energie $ T = \ frac {1} {2} M \ dot {x} ^ 2 $ ausgeübte Kraft

Deshalb, L=\frac{1}{2}(m+M)\dot{x}^2-\frac{1}{2}kx^2+Mgx Nächster $ \frac{\partial L}{\partial \dot{x}}=(m+M)\dot{x}$ $ \frac{d}{dt}\frac{\partial L}{\partial \dot{x}}=(m+M)\dot{x}$ $ \frac{\partial L}{\partial x}=-kx+Mg$ Mehr Lagrange-Bewegungsgleichung ((m+M)\ddot{x}=-kx+Mg or (m+M)\ddot{x_1}=kx_1 (1) Wobei $ x_1 = -x + Mg / k $

Da die allgemeine Lösung von Gleichung (1) $ A \ sin (\ omega t + \ alpha) $ ist x_1=A \sin(\omega t + \alpha) (2) \dot{x_1}=\omega A \cos(\omega t + \alpha) (3)

Wenn $ t = 0 $ $ x = 0 $, also $ x_1 = -Mg / k $, $ \ dot {x} = 0 $, also $ \ dot {x_1} = 0 $ x_1(0)=A \sin(\alpha)=-Mg/k \dot{x_1(0)}=\omega A \cos( \alpha)=0

\ cos (\ alpha) = 0 $ für $ \ omega A \ cos (\ alpha) = 0 \therefore \alpha=90^o

x_1(0)=A\sin(90^O)=A=-\frac{Mg}{k}, \therefore A=-Mg/k

\frac{\partial x_1}{\partial t} = -\omega \frac{Mg}{k} \cos(\omega t + \alpha)

x_1=-\frac{Mg}{k} \sin(\omega t+90^o) \frac{\partial x_1}{\partial t} = -\omega \frac{Mg}{k} \cos(\omega t + \alpha) \frac{\partial \dot{x_1}}{\partial t^2} = -\omega^2 \frac{Mg}{k} \sin(\omega t + \alpha)=x_1\omega^2 \ddot{x_1}=-x_1 \omega^2 Daher aus (1) -\omega^2(m+M)x_1=-kx_1 \omega=\sqrt{\frac{k}{m+M}}

x=\frac{M}{k}g(1-\cos\sqrt{\frac{k}{m+M}}t)

(1)

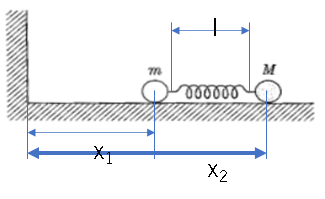
In relativen Koordinaten

Die Kraft, die auf das Versprechen wirkt

F=-kdx=k(l-x_2-x_1)

Potenzielle Energie

U=\frac{1}{2}k(l-x_2-x_1)^2

Übungsenergie

T=\frac{1}{2}m\dot{x_1}^2+\frac{1}{2}M\dot{x_2}^2

U=\frac{1}{2}k((l-x)^2

Wird sein. Deshalb,

L=T-U=\frac{1}{2}m\dot{x_1}^2+\frac{1}{2}M\dot{x_2}^2-\frac{1}{2}k((l-x)^2

In den Koordinaten des Schwerpunkts

Mit $ X = \ frac {mx_1 + Mx_2} {m + M} $ als Schwerpunkt ist $ x = x_2-x_1 $, $ \ dot {X} = \ frac {m \ dot {x_1} + M \ dot { x_2}} {m + M} $

\dot{X}^2=\frac{m^2\dot{x_1}^2+2mM\dot{x_1}\dot{x_2}+M^2\dot{x_2}^2}{(m+M)^2}

Weil es wird

T=\frac{1}{2}m\dot{x_1}^2+\frac{1}{2}M\dot{x_2}^2

\ \ =\frac{1}{2}(m+M)\dot{X}^2+\frac{1}{2}\frac{mM}{m+M}\dot{x}^2

Wird sein. Deshalb

L=\frac{1}{2}(m+M)\dot{X}^2+\frac{1}{2}\frac{mM}{m+M}\dot{x}^2-\frac{1}{2}((l-x_2-x_1)^2

(2)

Lagranges Bewegungsgleichung

$\frac{d}{dt}\frac{\partial L}{\partial \dot{x_i}} = \frac{\partial L}{\partial x_i} $

Weil es dargestellt wird durch

In relativen Koordinaten

M\ddot{x_2}=k(l-x)

In den Koordinaten des Schwerpunkts

(M+m)\ddot{X}=0

\frac{mM}{m+M}\ddot{x}=k(l-x)

(3) Das Trennen von zwei Objekten durch einen Abstand von $ l + a $ bedeutet $ x_2-x_1-l = a $. Wenn Sie also $ (M + m) \ ddot {X} = 0 $ einmal integrieren

\dot{X}=C

Wenn Sie wieder integrieren

X=Ct+D

Daher bewegt es sich linear mit der Zeit.

Ebenfalls,

$ \ frac {mM} {m + M} \ ddot {x} = -k ((l-x) $ bis $ A sin (wt + \ alpha) $

Wenn $ x_3 = x-l $, dann ist $ x_3 (t) = A sin (wt + \ alpha) $

Deshalb

\dot{x_3}(t)=-w A cos(wt+\alpha)

\ddot{x_3}(t)=-w^2 A sin(wt+\alpha)=-w^2 x_3

\frac{mM}{m+M}\ddot{x_3}=\frac{mM}{m+M}(-w^2 x_3)=-kx_3

Deshalb,

$w^2=\frac{k(m+M)}{mM} $

deshalb

$w=\sqrt{\frac{k(m+M)}{mM}} $

x_3=A sin (wt+\alpha)

Wenn $ t = 0 $

$ x_3 (0) = A sin (\ alpha) = 1 $ Daher ist $ A = a $

$ \ dot {x_3} (0) = w A cos (\ alpha) = 0 $ Daher ist $ \ alpha = 90 ^ o $

Deshalb

x_3=A sin (wt+90^o)=a cos(wt)=a cos(\sqrt{\frac{k(m+M)}{mM}}t)

\because

x=a cos(\sqrt{\frac{k(m+M)}{mM}}t)+l

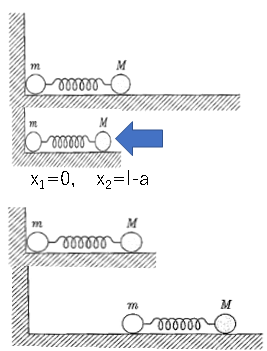
Bis sich das Versprechen von der Wand entfernt

In relativen Koordinaten

$T=\frac{1}{2}M\dot{x_2}^2 $

U=\frac{1}{2}l(l-x_2)

Wird sein. Deshalb

L=\frac{1}{2}M\dot{x_2}^2-\frac{1}{2}(l-x_2)

Lagranges Bewegungsgleichung

M\ddot{x_2}=-k(x_2-l)

Wenn $ x_3 = l-x_3 $

M\ddot{x_3}=kx_3

Deshalb,

x_3(t)=A sin (wt+\alpha)

\dot{x_3}(t)=-wA cos (wt+\alpha)

\ddot{x_3}(t)=-w^2A sin (wt+\alpha)=-w^2 x_3

M \ddot{x_3}=M(-w^2x_3)=-kx_3

\because \ w=\sqrt{\frac{k}{M}}

Wenn $ t = t_0 $

$ A sin (w t_0 + \ alpha) = a $ dann $ A = a $ und $ \ alpha = \ pi / 2 $

Deshalb,

w t_0 +\alpha=\pi \because t_0=\frac{\pi}{2}\sqrt{\frac{M}{k}}

Nach $ t_0 $ wird die Übung in (2) berechnet. Ersetzen Sie es jedoch durch $ t = t-t_0 $.

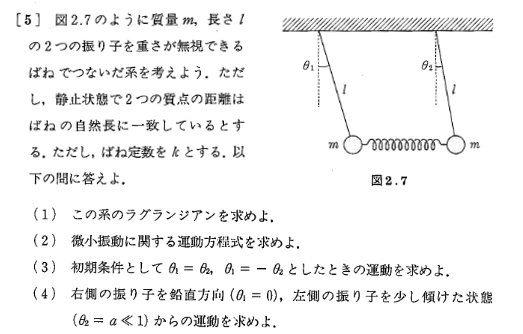
(1)

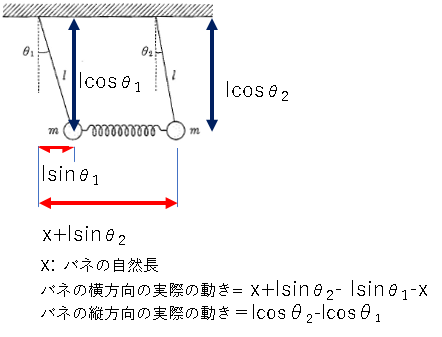
Position der Qualitätspunkte entlang der x-Achse: x_1=l \cdot sin \theta_1 x_2=x+l \cdot sin \theta_2

Position der Qualitätspunkte entlang der y-Achse: y_1=l \cdot cos \theta_1 y_2=l \cdot cos \theta_2

Daher ist die Zeitdifferenzierung erster Ordnung \dot{x_1}=-l \cdot cos \theta_1 \dot{\theta_1} \dot{x_2}=-l \cdot cos \theta_2 \dot{\theta_2} \dot{y_1}=l \cdot sin \theta_1 \dot{\theta_1} \dot{y_2}=l \cdot sin \theta_2 \dot{\theta_2} Daher ist die kinetische Energie $ \frac{1}{2}m(\dot{x_1}^2+\dot{x_2}^2+\dot{y_1}^2+\dot{y_2}^2)=$ $ \frac{1}{2}ml^2(\cdot cos^2 \theta_1 \dot{\theta_1}^2+\cdot cos^2 \theta_2 \dot{\theta_2}^2+ \cdot sin^2 \theta_1 \dot{\theta_1}^2+\cdot sin^2 \theta_2^2 \dot{\theta_2}^2)= \frac{1}{2}ml^2 (\dot{\theta_1}^2+\dot{\theta_2}^2)$

Die potentielle Energie der Feder U_1=\frac{1}{2}k(x_2-x_1)^2+(y_2-y_1)^2=\frac{1}{2}kl^2[(sin \theta_2-sin \theta_1)^2+(cos \theta_2-cos \theta_1)^2]

Die Energie der Position U_2=mg(y_1+y_2)=mgl(cos \theta_1+ cos \theta_2)

Deshalb Lagrange

L=\frac{1}{2}ml^2(\dot{\theta_1}^2+\dot{\theta_2}^2)+mgl(cos \theta_1+ cos \theta_2)-\frac{1}{2}kl^2[(sin \theta_2-sin \theta_1)^2+(cos \theta_2-cos \theta_1)^2]

(2) Da es sich um eine winzige Schwingung handelt, kann $ \ theta_1 <1, \ \ theta_2 <1, \ omega_g ^ 2 = g / l, \ omega_k ^ 2 = k / m $ als $ sin \ theta = \ theta $ angenähert werden. Von Die potentielle Energie der Feder U_1=\frac{1}{2}kl^2(\theta_2-\theta_1)^2 Ebenfalls, \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_1}}=ml\ddot{\theta_1} \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_2}}=ml\ddot{\theta_2} \frac{\partial U_1}{\partial \theta_1}=-kl^2(\theta_2-\theta_1) \frac{\partial U_1}{\partial \theta_2}=kl^2(\theta_2-\theta_1) \frac{\partial U_2}{\partial \theta_1}=-mgl sin\theta_1=-mgl\theta_1 \frac{\partial U_2}{\partial \theta_1}=-mgl sin \theta_2=-mgl\theta_2 Deshalb, \ddot{\theta_1}=\omega_g^2\theta_1-2\omega_k^2(\theta_2-\theta_1) \ddot{\theta_2}=\omega_g^2\theta_2+2\omega_k^2(\theta_2-\theta_1)

(3) Wenn der Anfangswert $ \ theta_1 = \ theta_2 $ ist, bewegen sich die beiden Qualitätspunkte in dieselbe Richtung. Addieren Sie daher die obigen Formeln. \ddot{\theta_1}+\ddot{\theta_2}=-\omega_g^2(\theta_1+\theta_2) Daher ist die Winkelfrequenz $ \ omega = \ omega_g $ Wenn der Anfangswert $ \ theta_1 = - \ theta_2 $ ist, bewegen sich die beiden Qualitätspunkte in entgegengesetzte Richtungen, sodass der Unterschied zwischen den obigen Gleichungen beträgt \ddot{\theta_1}-\ddot{\theta_2}=-\omega_g^2(\theta_1-\theta_2)-2\omega_k^2(\theta_1-\theta_2) Daher ist die Winkelfrequenz $ \ omega = \ sqrt {\ omega_g ^ 2 + 2 \ omega_k ^ 2} $ Wird sein.

(4) Da der Anfangswert $ \ theta_1 = 0, \ \ theta_2 = a $ ist, behält die Summe der Federwinkel $ a $ bei, so dass $ \ theta_1 + \ theta_2 = a $ die Winkeldifferenz ist Behalte $ \ theta_1- \ theta_2 = -a $.