[PYTHON]
Eine Fehlerbewertung sollte durchgeführt werden, diesmal wurde jedoch nur die Anzahl der Schleifen verwendet. Tonsignalverarbeitung mit CPython Python Teil 2 Adventskalender 2015 Tag 13 Es ist ein Artikel von. Meine übliche Arbeit besteht hauptsächlich darin, Algorithmen für die akustische Signalverarbeitung und die Implementierung von DSPs zu entwickeln. Beim Erstellen eines Algorithmus untersuche ich den Algorithmus jedoch zuerst mit Python und basierend auf den Ergebnissen C und C ++ Der Ablauf besteht darin, ein Echtzeitmodell zu erstellen, das auf einem PC ausgeführt wird. Überraschenderweise gibt es keinen umfassenden japanischen Artikel zur akustischen Signalverarbeitung. Daher möchte ich hier die Methode der akustischen Signalverarbeitung in Python und das Know-how, das ich bisher in meiner Arbeit verwendet habe, angemessen zusammenfassen. Inhaltsverzeichnis
- Motivation, akustische Signale mit Python zu verarbeiten
- Lesen und Schreiben von Audiodateien
- Ich möchte die Audioverarbeitung in Echtzeit durchführen
- Ich möchte den Frequenzgang anzeigen
- Ich möchte einen digitalen Filter entwerfen
- Ich möchte Nullen, Pole und Koeffizientenarrays b, a konvertieren
- Ich möchte ein digitales Filter auf ein Zeitreihensignal anwenden
- Ich möchte die Gruppenverzögerung berechnen
- Ich möchte die Zeitkorrelation berechnen (gegenseitige Korrelationsfunktion)
- Ich möchte einen Peak erkennen
Motivation zur Verarbeitung akustischer Signale mit Python
Eine Alternative zu Matlab. Um ehrlich zu sein, wird Matlab als Anlagevermögen behandelt, da es für die kommerzielle Nutzung mehr als 200.000 kostet und schwierig zu handhaben ist oder das Unternehmen es überhaupt nicht kaufen kann. Deshalb möchte ich etwas kostenlos tun.
Audiodateien lesen und schreiben
Informationen zum Lesen und Schreiben von Audiodateien finden Sie in dem Artikel 108 Möglichkeiten zum Umgang mit WAV-Dateien mit Python, den ich in der Vergangenheit in meinem Blog geschrieben habe. Es ist zusammengefasst. Persönlich habe ich PySoundFile heutzutage häufiger verwendet. Das Folgende ist ein Prozess, der nur FFTs mit 1/2 Überlappung, IFFTs und Wiederherstellungen ausführt.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import sys
import numpy as np
import scipy.fftpack as fft
import matplotlib.pyplot as plt
import soundfile as sf
if __name__ == '__main__':
plt.close("all")
#WAV-Datei lesen
filename = sys.argv[1]
wav, fs = sf.read(filename)
#Im Fall von Stereo 2ch wird es in Lch und Rch unterteilt
wav_l = wav[:, 0]
wav_r = wav[:, 1]
#Mono-Eingang
xs = (0.5 * wav_l) + (0.5 * wav_r)
n_len = len(xs)
n_fft = 128
n_overlap = 2
n_shift = n_fft / n_overlap
#Zwischenpuffer
zs = np.zeros(n_len)
Zs = np.zeros(n_fft)
#Ausgabepuffer
ys = np.zeros(n_len)
#Fensterfunktion
window = np.hanning(n_fft)
# FFT & IFFT
for start in range(0, n_len - n_shift, n_shift):
xs_cut = xs[start: start + n_fft]
xs_win = xs_cut * window
Xs = fft.fft(xs_win, n_fft)
# some signal processing
Zs = Xs
zs = fft.ifft(Zs, n_fft)
# write output buffer
ys[start: start + n_fft] += np.real(zs)
#10 Sekunden Handlung von Anfang an
fig = plt.figure(1, figsize=(8, 10))
ax = fig.add_subplot(211)
ax.plot(xs[:fs*10])
ax.set_title("input signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax = fig.add_subplot(212)
ax.plot(ys[:fs*10])
ax.set_title("output signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
plt.show()
Handlungsbeispiel

Ich möchte die Audioverarbeitung in Echtzeit durchführen
Es ist einfach, die Python-Bindung von PortAudio PyAudio zu verwenden.
Hier ist ein Beispiel für das Puffern des Mikrofoneingangssignals in einer globalen Variablen in der Rückrufmethode und das Speichern in einer WAV-Datei. Listen Sie zunächst die verfügbaren Geräte auf.
pyaudio_print_devices.py
#!/usr/bin/env python
# vim:fileencoding=utf-8
import pyaudio as pa
if __name__ == "__main__":
#Verfügbare Geräte auflisten
p_in = pa.PyAudio()
print "device num: {0}".format(p_in.get_device_count())
for i in range(p_in.get_device_count()):
print p_in.get_device_info_by_index(i)
$ python pyaudio_print_devices.py
device num: 2
{'defaultSampleRate': 44100.0, 'defaultLowOutputLatency': 0.01, 'defaultLowInputLatency': 0.00199546485260771, 'maxInputChannels': 2L, 'structVersion': 2L, 'hostApi': 0L, 'index': 0, 'defaultHighOutputLatency': 0.1, 'maxOutputChannels': 0L, 'name': u'Built-in Microph', 'defaultHighInputLatency': 0.012154195011337868}
{'defaultSampleRate': 44100.0, 'defaultLowOutputLatency': 0.004693877551020408, 'defaultLowInputLatency': 0.01, 'maxInputChannels': 0L, 'structVersion': 2L, 'hostApi': 0L, 'index': 1, 'defaultHighOutputLatency': 0.014852607709750568, 'maxOutputChannels': 2L, 'name': u'Built-in Output', 'defaultHighInputLatency': 0.1}
Wenn Sie sich "maxInputChannels" ansehen, können Sie sehen, dass dies das Eingabegerät ist, da das erste Gerät 2L und der "Name" u'Built-in Microph 'ist.
Als nächstes folgt ein Skript, das den Mikrofoneingang in einer WAV-Datei speichert. PyAudio verfügt über eine nicht blockierende Verarbeitungsmethode, die einen Rückruf verwendet, und eine blockierende Verarbeitungsmethode, die keinen Rückruf verwendet. Hier wird die frühere Methode, die einen Rückruf verwendet, für die Verarbeitung verwendet. Bei der Rückrufmethode wird das Eingangssignal von kurz in einen Gleitkommawert von -1,0 bis 1,0 umgewandelt und einfach mit der globalen Variablen xs kombiniert.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import time
import numpy as np
import soundfile as sf
import pyaudio as pa
# global
xs = np.array([])
def callback(in_data, frame_count, time_info, status):
global xs
in_float = np.frombuffer(in_data, dtype=np.int16).astype(np.float)
in_float[in_float > 0.0] /= float(2**15 - 1)
in_float[in_float <= 0.0] /= float(2**15)
xs = np.r_[xs, in_float]
return (in_data, pa.paContinue)
if __name__ == "__main__":
# pyaudio
p_in = pa.PyAudio()
py_format = p_in.get_format_from_width(2)
fs = 16000
channels = 1
chunk = 1024
use_device_index = 0
#Eingabestream erstellen
in_stream = p_in.open(format=py_format,
channels=channels,
rate=fs,
input=True,
frames_per_buffer=chunk,
input_device_index=use_device_index,
stream_callback=callback)
in_stream.start_stream()
# input loop
#Geben Sie etwas ein und beenden Sie
while in_stream.is_active():
c = raw_input()
if c:
break
time.sleep(0.1)
else:
in_stream.stop_stream()
in_stream.close()
#Eingangssignal speichern
sf.write("./pyaudio_output.wav", xs, fs)
p_in.terminate()
Tun Sie dies und geben Sie etwas ein, um aus der while-Schleife auszubrechen und xs in "./pyaudio_output.wav" zu speichern. Wenn Sie beim Öffnen von p_in output = True anstelle von input = True setzen, wird es als Wiedergabegerät behandelt. Weitere Informationen finden Sie im Beispiel unten auf der PyAudio-Seite.
Ich möchte den Frequenzgang anzeigen
In scipy.signal gibt es eine Methode, die nach dem Frequenzgang [freqz] fragt (https://docs.scipy.org/doc/scipy-0.16.0/reference/generated/scipy.signal.freqz.html). Wie ich in Artikel geschrieben habe, ist der Teil, in dem das Polynom durch np.polyval berechnet wird, schwer, und wenn es kontinuierlich ausgeführt wird, ist die Langsamkeit langsam. Es fällt wirklich auf. Daher können Sie, wie ich im vorherigen Artikel geschrieben habe, den Frequenzgang ermitteln, indem Sie die folgende Methode definieren, die scipy.fftpack verwendet.
def my_freqz(b, a=[1], worN=None):
import scipy.fftpack as fft
lastpoint = np.pi
N = 512 if worN is None else worN
w = np.linspace(0.0, lastpoint, N, endpoint=False)
h = fft.fft(b, 2 * N)[:N+1] / fft.fft(a, 2 * N)[:N+1]
return w, h
Angenommen, Sie möchten die Antwort eines einfachen Verbesserungsfilters b = [1.0, -0.97] und eines De-Enfasis-Filters b = [1.0], a = [1.0, -0.97], der seine Eigenschaften wiederherstellt. Sie können jeden Frequenzgang mit einem Skript wie dem folgenden darstellen: Beachten Sie, dass die horizontale Achse beim Zeichnen 0 bis FS / 2 beträgt, da der Bereich von w 0 bis π beträgt.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
def my_freqz(b, a=[1], worN=None):
import scipy.fftpack as fft
lastpoint = np.pi
N = 512 if worN is None else worN
w = np.linspace(0.0, lastpoint, N, endpoint=False)
h = fft.fft(b, 2 * N)[:N] / fft.fft(a, 2 * N)[:N]
return w, h
if __name__ == "__main__":
plt.close("all")
N = 1024
FS = 16000.0
EMP = -0.97
b_emp = [1.0, EMP]
a_emp = [1.0]
b_deemp = [1.0]
a_deemp = [1.0, EMP]
(w_emp, h_emp) = my_freqz(b_emp, a_emp, worN=N)
(w_deemp, h_deemp) = my_freqz(b_deemp, a_deemp, worN=N)
fig = plt.figure(1)
ax = fig.add_subplot(2, 1, 1)
ax.semilogx(w_emp * (FS / 2.0) / np.pi,
20.0 * np.log10(np.abs(h_emp)))
ax.grid()
ax.set_xlabel("frequency response [Hz]")
ax.set_ylabel("power [dB]")
ax = fig.add_subplot(2, 1, 2)
ax.semilogx(w_deemp * (FS / 2.0) / np.pi,
20.0 * np.log10(np.abs(h_deemp)))
ax.grid()
ax.set_xlabel("frequency response [Hz]")
ax.set_ylabel("power [dB]")
plt.show()
Dadurch wird eine Antwort ähnlich der folgenden dargestellt.

Ich möchte einen digitalen Filter entwerfen
In scipy.signal werden verschiedene Filterdesignfunktionen bereitgestellt, einschließlich FIR-Filterdesignfunktionen (firwin, firwin2, remez usw.) und matlab-kompatiblen IIR-Designfunktionen (Butter, Buttord, cheby1, cheb1ord usw.). ..
Um beispielsweise LPF, BPF, HPF mithilfe von Firwin zu finden, können Sie das folgende Skript verwenden.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sg
def my_freqz(b, a=[1], worN=None):
import scipy.fftpack as fft
lastpoint = np.pi
N = 512 if worN is None else worN
w = np.linspace(0.0, lastpoint, N, endpoint=False)
h = fft.fft(b, 2 * N)[:N] / fft.fft(a, 2 * N)[:N]
return w, h
if __name__ == '__main__':
plt.close("all")
fs = 48000.0
num_tap = 1024
lpf_cutoff_hz = 400.0
hpf_cutoff_hz = 1000.0
lpf_cutoff = lpf_cutoff_hz / (fs/2.0)
bpf_band = np.array([lpf_cutoff_hz, hpf_cutoff_hz]) / (fs/2.0)
hpf_cutoff = hpf_cutoff_hz / (fs/2.0)
win = "hann"
lpf = sg.firwin(num_tap, lpf_cutoff, window=win)
bpf = sg.firwin(num_tap, bpf_band, pass_zero=False, window=win)
hpf = sg.firwin(num_tap, [hpf_cutoff, 0.9999], pass_zero=False, window=win)
# plot filter response
w, lpf_h = my_freqz(lpf, worN=num_tap)
w, bpf_h = my_freqz(bpf, worN=num_tap)
w, hpf_h = my_freqz(hpf, worN=num_tap)
lpf_amp = np.abs(lpf_h)
bpf_amp = np.abs(bpf_h)
hpf_amp = np.abs(hpf_h)
fig = plt.figure(1)
ax = fig.add_subplot(111)
ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(lpf_amp), "bx-")
ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(bpf_amp), "yx-")
ax.semilogx(fs * w/(2 * np.pi), 20.0*np.log10(hpf_amp), "rx-")
ax.set_xlim([0.0, 24000.0])
ax.set_ylim([-150.0, 10.0])
ax.set_ylabel("power [dB]")
ax.set_xlabel("frequency [Hz]")
ax.grid()
ax.legend(["lpf", "bpf", "hpf"], loc="best")
plt.show()
Als Ergebnis wird das folgende Diagramm dargestellt.
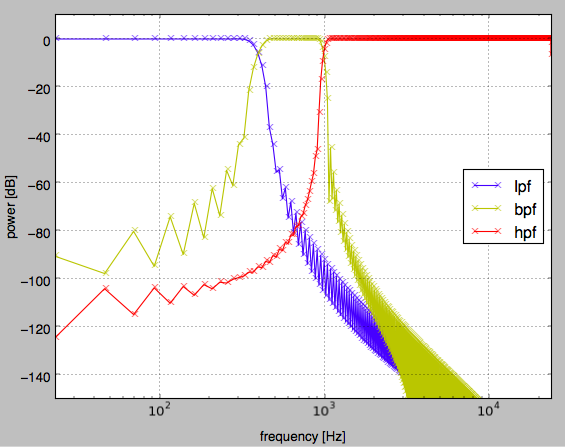
Wenn Sie einen Filter vom Typ Biquad (sekundärer IIR) entwerfen möchten, können Sie auch Ihre eigene Funktion gemäß EQ Cookbook erstellen. Im Fall eines Peaking-EQ sieht es beispielsweise wie folgt aus (Rückgabewerte sind b, a).
def peaking_eq(q, gain, f, fs):
A = 10 ** (gain / 40.0)
w0 = 2.0 * np.pi * f / fs
alpha = np.sin(w0) / (2.0 * q)
b = [(1.0 + alpha * A), (-2.0 * np.cos(w0)), (1.0 - alpha * A)]
a = [(1.0 + alpha / A), (-2.0 * np.cos(w0)), (1.0 - alpha / A)]
return (np.array(b) / a[0]), (np.array(a) / a[0])
Ich möchte Nullen, Pole und Koeffizientenarrays b, a ## konvertieren
tf2zpk und zpk2tf /doc/scipy/reference/generated/scipy.signal.zpk2tf.html#scipy.signal.zpk2tf) wird verwendet. tf steht für Zeitfilter und zpk steht für Null, Pol, k (Verstärkung). Wenn Sie einen IIR-Filter 6. Ordnung usw. herstellen und ihn so wie er ist in C montieren, kann er aufgrund eines Fehlers abweichen. Wenn Sie also den Nullpunkt und den Pol kennen, können Sie den Filter in 3 Stufen des IIR-Filters 2. Ordnung zerlegen. ..
Ich möchte ein digitales Filter auf ein Zeitreihensignal anwenden
Es gibt zwei Möglichkeiten, das entworfene digitale Filter auf ein Zeitreihensignal anzuwenden. [Scipy.signal.lfilter](https://docs.scipy.org/doc/scipy-0.16.0/reference/generated/scipy.signal.lfilter.html#scipy.signal] ist die Methode, die die Faltung im Zeitbereich verwendet. [scipy.signal.fftconvolve](https://docs.scipy.org/doc/scipy-0.16.0/reference/generated], um die Faltung des Filters als sofortigen Prozess im Frequenzbereich zu verarbeiten. /scipy.signal.fftconvolve.html#scipy.signal.fftconvolve) wird verwendet. Unten finden Sie ein Skript, das die Ergebnisse der Anwendung von lpf als Eingabe mit jeder Methode darstellt.
#!/usr/bin/env python
# vim:fileencoding=utf-8
import sys
import scipy.signal as sg
import matplotlib.pyplot as plt
import soundfile as sf
if __name__ == '__main__':
plt.close("all")
#WAV-Datei lesen
filename = sys.argv[1]
wav, fs = sf.read(filename)
#Im Fall von Stereo 2ch wird es in Lch und Rch unterteilt
wav_l = wav[:, 0]
wav_r = wav[:, 1]
#Mono-Eingang
xs = (0.5 * wav_l) + (0.5 * wav_r)
#LPF-Design
num_tap = 1024
lpf_cutoff_hz = 400.0
lpf_cutoff = lpf_cutoff_hz / (fs/2.0)
win = "hann"
lpf = sg.firwin(num_tap, lpf_cutoff, window=win)
#Linearfilter anwenden
ys = sg.lfilter(lpf, [1.0], xs)
#Anwendung des Frequenzbereichsfilters
zs = sg.fftconvolve(xs, lpf, mode="same")
#10 Sekunden Handlung von Anfang an
fig = plt.figure(1)
ax = fig.add_subplot(311)
ax.plot(xs[:fs*10])
ax.set_title("input signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax = fig.add_subplot(312)
ax.plot(ys[:fs*10])
ax.set_title("lfilter output signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
ax = fig.add_subplot(313)
ax.plot(ys[:fs*10])
ax.set_title("fftconvolve output signal")
ax.set_xlabel("time [pt]")
ax.set_ylabel("amplitude")
fig.set_tight_layout(True)
plt.show()

Ich möchte die Gruppenverzögerung berechnen
Bei der Betrachtung der Eigenschaften eines Allpassfilters, bei dem es sich um einen Filter handelt, der nur die Phase ändert, ohne die Amplitude zu ändern, insbesondere indem die [Gruppenverzögerung](https://ja.wikipedia.org/wiki/ Gruppenverzögerung und Phasenverzögerung) für jede Frequenz ermittelt wird Sie können sehen, wie hoch die Verzögerung der Sample-Einheit ist. Scipy.signal verfügt jedoch nicht über die in matlab vorhandene Funktion grpdelay. Daher müssen Sie grpdelay in geeigneter Weise selbst implementieren. Daher werden wir hier ein Verfahren einführen, um die Differenzierung jeder Frequenz durch Approximation basierend auf der Differenz erster Ordnung zu erhalten.
def grpdelay(w, h, fs):
"""Berechnung der Gruppenverzögerungseigenschaften durch einfache Näherung erster Ordnung(Ergebnisse sind Stichprobeneinheiten).. Da es durch die Differenz berechnet wird, wird die Dimension um eins reduziert, sodass das letzte Element immer auf 0 gesetzt wird. w ist die normalisierte Frequenz und h ist die Frequenzcharakteristik, die w entspricht"""
return -1.0 * np.r_[np.diff(np.unwrap(np.angle(h))) / np.diff(w), [0]]
Es ist nicht genau der Algorithmus, der in matlabs grpdelay verwendet wird, aber es reicht aus, wenn Sie nur die groben Ergebnisse sehen möchten.
Ich möchte die Zeitkorrelation berechnen (gegenseitige Korrelationsfunktion)
scipy.signal hat kein xcorr, wie es in matlab genannt wird. Da xcorr das Kreuzspektrum im Frequenzbereich basierend auf dem Satz von Wiener Hintin findet und die Interkorrelationsfunktion durch inverse Transformation findet, kann es die Interkorrelationsfunktion schneller finden als die Produktsummenberechnung im Zeitbereich.
Im Folgenden wird die xcorr-Methode definiert, die der my_correlate-Methode entspricht, die die gegenseitige Korrelationsfunktion im Zeitbereich findet. Ceil2 ist eine Methode, um den Wert der Potenz von 2 zu ermitteln, der gleich oder größer als das Argument ist. Wenn das Argument die Potenz von 2 ist, wird x & (x -1) zu 0, sodass der Wert des Arguments zurückgegeben wird. Das Argument wird in eine Zeichenfolge mit binärer Notation konvertiert, der andere Wert als das höchstwertige Bit wird in der Zeichenfolgenverarbeitung auf 0 gesetzt, und der Wert, der durch Verschieben der Zahl um 1 Bit nach links erhalten wird, wird erhalten.
def my_correlate(sig, ref, lag=None):
lag = np.alen(ref) / 2 if lag is None else lag
corrs = []
sig_len = np.alen(sig)
sig_norm = np.sqrt(np.dot(sig, sig))
ref_norm = np.sqrt(np.dot(ref, ref))
sig_expand = np.r_[np.zeros(lag), sig, np.zeros(lag)]
center = lag
for begin in range(center - lag, center + lag + 1):
sig_cut = sig_expand[begin :begin + sig_len]
corrs.append(np.dot(sig_cut, ref))
return np.array(corrs) / (sig_norm * ref_norm)
def ceil2(x):
new_x = 0
if (x & (x - 1)) == 0:
new_x = x
else:
bit_str = bin(x)
head_bit = bit_str[2]
tail_bits = bit_str[3:].replace("1", "0")
new_bit_str = "0b" + head_bit + tail_bits
new_x = int(new_bit_str, 2) << 1
return new_x
def xcorr(sig, ref, lag=None):
import scipy.fftpack as fft
lag = 1024 if lag is None else lag
sig_len = np.alen(sig)
nfft = ceil2(sig_len)
sig_norm = np.sqrt(np.dot(sig, sig))
ref_norm = np.sqrt(np.dot(ref, ref))
sig_ = sig / sig_norm
ref_ = ref / ref_norm
X = fft.fft(sig_, nfft)
Y = fft.fft(ref_, nfft)
# ifft to calculate correlation
corr_p = np.real(fft.ifft(X * np.conjugate(Y), nfft))
corr_m = np.real(fft.ifft(Y * np.conjugate(X), nfft))
# concat
corr = np.r_[corr_m[1:lag+1][::-1], corr_p[:lag+1]]
return corr
Tatsächlich müssen wir bei der Verwendung von FFT den Einfluss der Patrouille berücksichtigen, sodass ich der Meinung bin, dass in den oben genannten Punkten Verbesserungspotenzial besteht. Referenz: http://www.ikko.k.hosei.ac.jp/~matlab/xcorr.pdf
Ich möchte den Peak ## erkennen
scipy.signal hat auch eine Methode namens find_peaks_cwt, die jedoch bequemer ist. Ich wollte eine Lichtfunktion, also benutze ich die folgende Methode.
def find_peaks(a, amp_thre, local_width=1, min_peak_distance=1):
"""
Der Peak wird aus dem Array erfasst, indem der Schwellenwert, die Fensterbreite zum Bestimmen des Maximums / Minimums und der minimale Abstand zwischen den Peaks angegeben werden.
Intern wird der Abstand zwischen Peaks berechnet, indem zwischen positiven und negativen Peaks unterschieden wird, sodass nahe positive und negative Peaks erkannt werden.
:rtype (int, float)
:return tuple (ndarray of peak indices, ndarray of peak value)
"""
# generate candidate indices to limit by threthold
idxs = np.where(np.abs(a) > amp_thre)[0]
# extend array to decide local maxima/minimum
idxs_with_offset = idxs + local_width
a_extend = np.r_[[a[0]] * local_width, a, [a[-1]] * local_width]
last_pos_peak_idx = 0
last_neg_peak_idx = 0
result_idxs = []
for i in idxs_with_offset:
is_local_maximum = (a_extend[i] >= 0 and
a_extend[i] >= np.max(a_extend[i - local_width: i + local_width + 1]))
is_local_minimum = (a_extend[i] < 0 and
a_extend[i] <= np.min(a_extend[i - local_width: i + local_width + 1]))
if (is_local_maximum or is_local_minimum):
if is_local_minimum:
if i - last_pos_peak_idx > min_peak_distance:
result_idxs.append(i)
last_pos_peak_idx = i
else:
if i - last_neg_peak_idx > min_peak_distance:
result_idxs.append(i)
last_neg_peak_idx = i
result_idxs = np.array(result_idxs) - local_width
return (result_idxs, a[result_idxs])
das ist alles
Ich habe das Gefühl, dass ich noch etwas zu schreiben habe, aber das war's. Das nächste Mal ist @kimihiro_n.
Recommended Posts