Einführung

Dieser Artikel verwendet Python 2.7, Numpy 1.11, Scipy 0.17, Scikit-Learn 0.18, Matplotlib 1.5, Seaborn 0.7, Pandas 0.17. Es wurde bestätigt, dass es an einem Jupiter-Notebook funktioniert. (Bitte ändern Sie% matplotlib inline entsprechend) Ich verweise auf den Artikel von Sklearns Manifold learning.

Eine als Lernen mit mehreren Objekten bezeichnete Technik wird anhand eines Beispiels sklearn digits erläutert. Insbesondere ist t-SNE ein Verfahren zur Visualisierung mehrdimensionaler Daten, das manchmal in Kaggle und dergleichen verwendet wird. Zusätzlich zur Visualisierung kann die Genauigkeit einfacher Klassifizierungsprobleme verbessert werden, indem die Originaldaten und die komprimierten Daten kombiniert werden.

Inhaltsverzeichnis

Datengenerierung
Dimensionsreduzierung mit Schwerpunkt auf linearen Elementen
1. Random Projection
2. PCA
3. Linear Discriminant Analysis
Dimensionsreduzierung unter Berücksichtigung nichtlinearer Komponenten
1. Isomap
2. Locally Linear Embedding
3. Modified Locally Linear Embedding
4. Hessian Eigenmapping
5. Spectral Embedding
6. Local Tangent Space Alignment
7. Multi-dimensional Scaling
8. t-SNE
9. Random Forest Embedding

1. Datengenerierung

Verwenden Sie die Beispieldaten von sklearn. Dieses Mal werden wir die Zahlen mithilfe des Ziffern-Datasets gruppieren. Laden und überprüfen Sie zunächst die Daten.

`load_digit.py`


from time import time

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import offsetbox
from sklearn import (manifold, datasets, decomposition, ensemble,
                     discriminant_analysis, random_projection)

digits = datasets.load_digits(n_class=6)
X = digits.data
y = digits.target
n_samples, n_features = X.shape
n_neighbors = 30

n_img_per_row = 20
img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))
for i in range(n_img_per_row):
    ix = 10 * i + 1
    for j in range(n_img_per_row):
        iy = 10 * j + 1
        img[ix:ix + 8, iy:iy + 8] = X[i * n_img_per_row + j].reshape((8, 8))

plt.imshow(img, cmap=plt.cm.binary)
plt.xticks([])
plt.yticks([])
plt.title('A selection from the 64-dimensional digits dataset')

Bereiten Sie eine Funktion zum Zuordnen von Zifferndaten vor. Dies ist nicht das Thema dieses Artikels. Überspringen Sie es, wenn Sie sich nicht sicher sind.

def plot_embedding(X, title=None):
    x_min, x_max = np.min(X, 0), np.max(X, 0)
    X = (X - x_min) / (x_max - x_min)

    plt.figure()
    ax = plt.subplot(111)
    for i in range(X.shape[0]):
        plt.text(X[i, 0], X[i, 1], str(digits.target[i]),
                 color=plt.cm.Set1(y[i] / 10.),
                 fontdict={'weight': 'bold', 'size': 9})

    if hasattr(offsetbox, 'AnnotationBbox'):
        # only print thumbnails with matplotlib > 1.0
        shown_images = np.array([[1., 1.]])  # just something big
        for i in range(digits.data.shape[0]):
            dist = np.sum((X[i] - shown_images) ** 2, 1)
            if np.min(dist) < 4e-3:
                # don't show points that are too close
                continue
            shown_images = np.r_[shown_images, [X[i]]]
            imagebox = offsetbox.AnnotationBbox(
                offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r),
                X[i])
            ax.add_artist(imagebox)
    plt.xticks([]), plt.yticks([])
    if title is not None:
        plt.title(title)

2. Dimensionsreduzierung mit Schwerpunkt auf linearen Komponenten

Das hier vorgestellte Verfahren hat geringe Rechenkosten und eine hohe Vielseitigkeit und wird häufig verwendet. Zum Beispiel ist PCA eine sehr bequeme Methode, mit der die Korrelation von Daten extrahiert werden kann. Diese Methoden werden auf vielen Websites ausführlich erläutert. Lassen Sie uns einen kurzen Blick darauf werfen.

2.1. Random Projection Ich habe 64 dimensionale numerische Daten in 1. Die grundlegendste Methode zur Abbildung solcher hochdimensionaler Daten ist die Zufallsprojektion. Unter Verwendung eines sehr einfachen Verfahrens werden die Elemente der Matrix R, die M-dimensionale Daten auf abbildbare N-dimensionale Daten abbildet, mit Zufallszahlen gesetzt. Der Vorteil sind die geringen Berechnungskosten.

print("Computing random projection")
rp = random_projection.SparseRandomProjection(n_components=2, random_state=42)
X_projected = rp.fit_transform(X)
plot_embedding(X_projected, "Random Projection of the digits")
#plt.scatter(X_projected[:, 0], X_projected[:, 1])

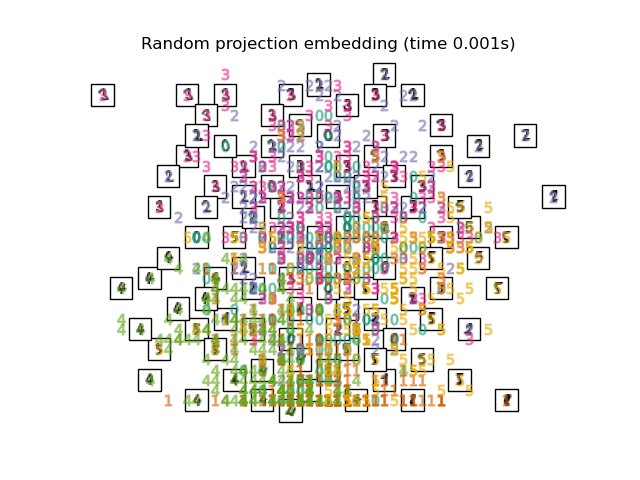
2.2. PCA Karte mit PCA, einer allgemeinen Methode zur Dimensionskomprimierung. Extrahieren Sie die Korrelationskomponente zwischen Variablen. Die verwendete Funktion ist die abgeschnittene SVD von sklearn, und der Unterschied zur PCA scheint darin zu bestehen, ob die Eingabedaten normalisiert werden sollen.

print("Computing PCA projection")
t0 = time()
X_pca = decomposition.TruncatedSVD(n_components=2).fit_transform(X)
plot_embedding(X_pca,
               "Principal Components projection of the digits (time %.2fs)" %
               (time() - t0))

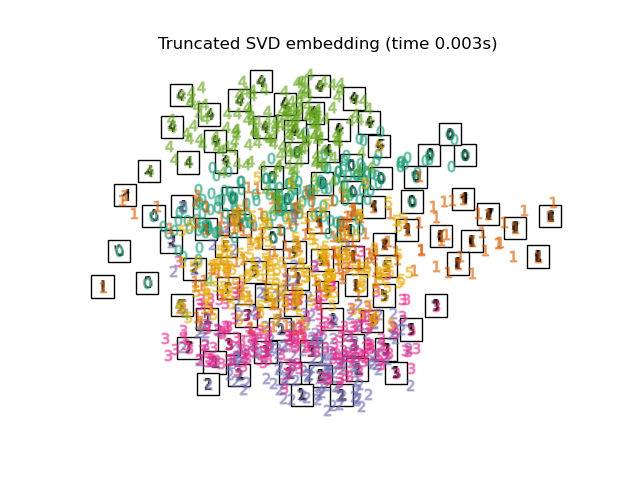
2.3. Linear Discriminant Analysis Die Dimensionsreduzierung wird durch Lineare Unterscheidungsklassifizierung durchgeführt. Der Maharanobis-Abstand wird unter der Annahme verwendet, dass jede Variable eine multivariate Normalverteilung und dieselbe Gruppe dieselbe Kovarianzmatrix aufweist. Ähnlich wie bei PCA, aber dies ist überwachtes Lernen.

print("Computing Linear Discriminant Analysis projection")
X2 = X.copy()
X2.flat[::X.shape[1] + 1] += 0.01  # Make X invertible
t0 = time()
X_lda = discriminant_analysis.LinearDiscriminantAnalysis(n_components=2).fit_transform(X2, y)
plot_embedding(X_lda,
               "Linear Discriminant projection of the digits (time %.2fs)" %
               (time() - t0))

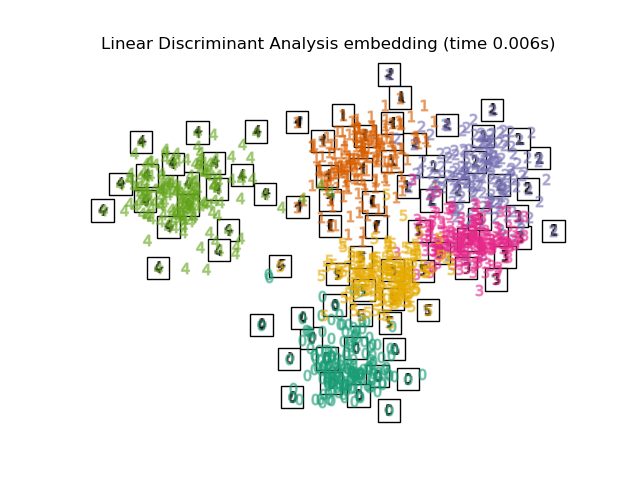
3. Dimensionsreduzierung unter Berücksichtigung nichtlinearer Komponenten

Die drei zuvor eingeführten Methoden eignen sich nicht zum Reduzieren der Dimensionen von Daten mit einer hierarchischen Struktur und Daten, die nichtlineare Komponenten enthalten. Hier werden wir eine zweidimensionale Darstellung nichtlinearer Korrelationsdaten wie z. B. Swiss Roll einführen.

download (2).png

3.1. Isomap Isomap ist eine der Methoden zur Dimensionsreduzierung und Clusterbildung unter Berücksichtigung der Nichtlinearität. Die mehrdimensionale Skalierung basiert auf der Berechnung des Abstands, der entlang der Form der Sorte gemessen wird. Es kann mit der Isomap-Funktion von Sklearn ausgeführt werden. BallTree wird bei der Berechnung der gemessenen Entfernung verwendet.

print("Computing Isomap embedding")
t0 = time()
X_iso = manifold.Isomap(n_neighbors, n_components=2).fit_transform(X)
print("Done.")
plot_embedding(X_iso,
               "Isomap projection of the digits (time %.2fs)" %
               (time() - t0))

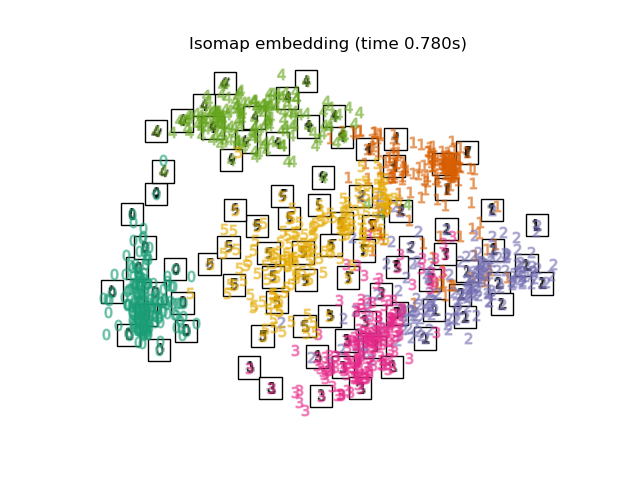
3.2. Locally Linear Embedding (LLE) Insgesamt sogar eine Sorte, die Nichtlinearität beinhaltet. Eine Dimensionsreduktionsmethode, die auf der Intuition der Linearität basiert, wenn sie lokal betrachtet wird. Das 0-Label scheint hervorgehoben zu sein, aber die anderen Labels sind durcheinander.

print("Computing LLE embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='standard')
t0 = time()
X_lle = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_lle,
               "Locally Linear Embedding of the digits (time %.2fs)" %
               (time() - t0))

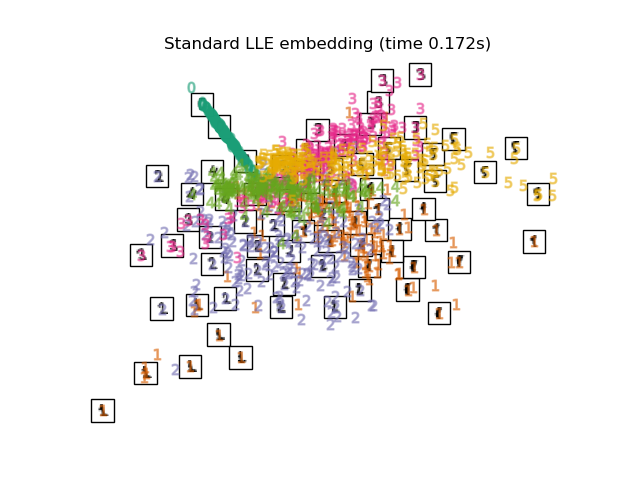
3.3. Modified Locally Linear Embedding Ein Algorithmus, der das Regularisierungsproblem verbessert, das ein Problem von LLE ist. 0 Etiketten sind eindeutig klassifiziert. Die 4, 1, 5 Beschriftungen scheinen ebenfalls gut zugeordnet zu sein.

print("Computing modified LLE embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='modified')
t0 = time()
X_mlle = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_mlle,
               "Modified Locally Linear Embedding of the digits (time %.2fs)" %
               (time() - t0))

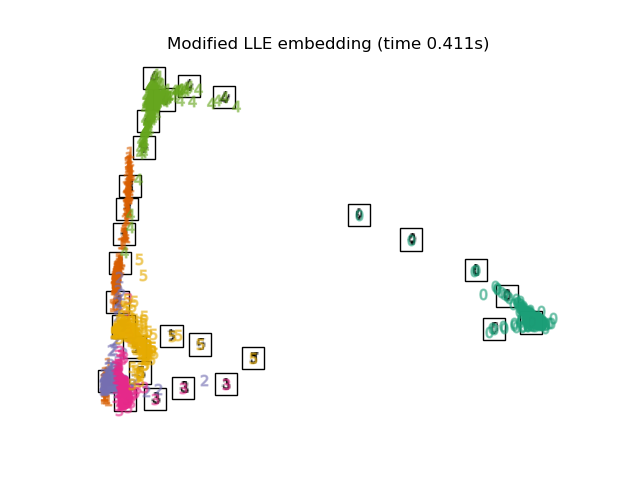
3.4. Hessian LLE Embedding Ein Algorithmus, der das Regularisierungsproblem verbessert, das ein Problem von LLE ist. Teil 2

print("Computing Hessian LLE embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='hessian')
t0 = time()
X_hlle = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_hlle,
               "Hessian Locally Linear Embedding of the digits (time %.2fs)" %
               (time() - t0))

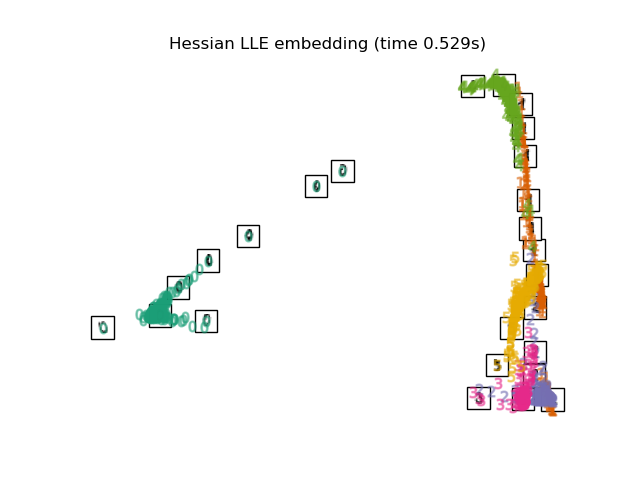
3.5. Spectral Embedding Es ist eine Komprimierungsmethode, die auch als Laplace-Eigenkarten bezeichnet wird. Ich habe den technischen Inhalt nicht untersucht, aber es scheint, dass ich die Spektralgraphentheorie verwende. Die Form der Abbildung unterscheidet sich von LLE, MLLE, HLLE, aber der Abstand und die Dichte zwischen den Markierungsgruppen scheinen ähnlich zu sein.

print("Computing Spectral embedding")
embedder = manifold.SpectralEmbedding(n_components=2, random_state=0,
                                      eigen_solver="arpack")
t0 = time()
X_se = embedder.fit_transform(X)

plot_embedding(X_se,
               "Spectral embedding of the digits (time %.2fs)" %
               (time() - t0))

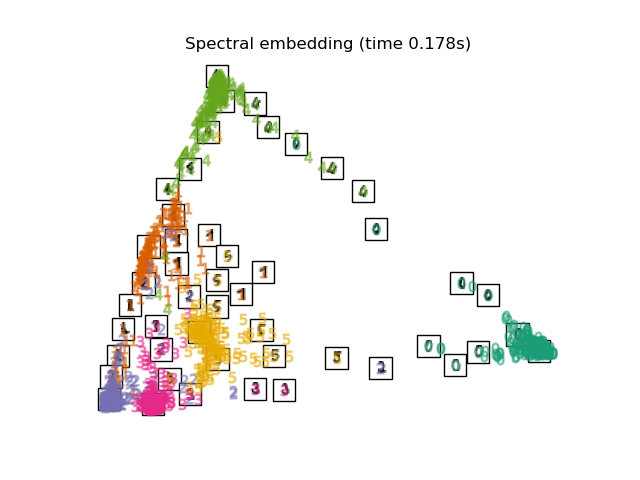
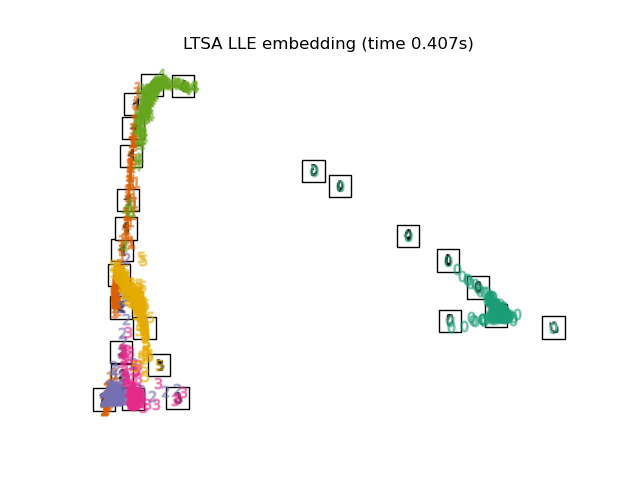
3.6. Local Tangent Space Alignment

Das Ergebnis ist wie das Umkehren von MLLE und HLLE. Die Klassifizierungsergebnisse sind ähnlich.

print("Computing LTSA embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='ltsa')
t0 = time()
X_ltsa = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_ltsa,
               "Local Tangent Space Alignment of the digits (time %.2fs)" %
               (time() - t0))

3.7. Multi-dimensional Scaling (MDS) [Konstruktionsmethode für mehrdimensionale Skalen](https://ja.wikipedia.org/wiki/%E5%A4%9A%E6%AC%A1%E5%85%83%E5%B0%BA%E5%BA%A6 Es handelt sich um eine Komprimierungsmethode namens% E6% A7% 8B% E6% 88% 90% E6% B3% 95). MDS selbst scheint ein allgemeiner Begriff zu sein, der mehrere Methoden zusammenfasst, aber die Details sind nicht besonders zusammengefasst.

print("Computing MDS embedding")
clf = manifold.MDS(n_components=2, n_init=1, max_iter=100)
t0 = time()
X_mds = clf.fit_transform(X)
print("Done. Stress: %f" % clf.stress_)
plot_embedding(X_mds,
               "MDS embedding of the digits (time %.2fs)" %
               (time() - t0))

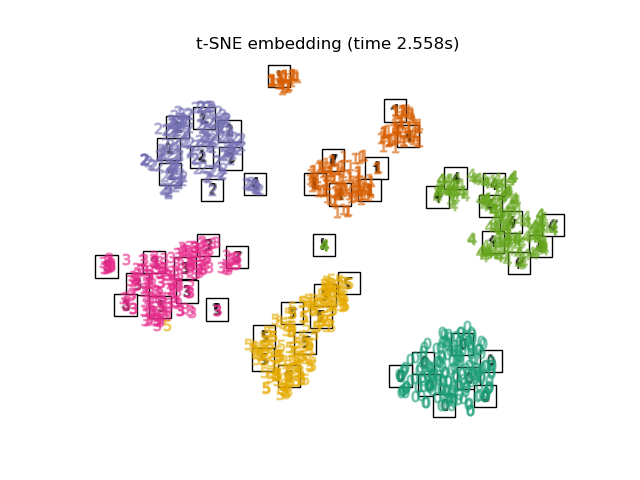
3.8. t-distributed Stochastic Neighbor Embedding (t-SNE) Dies ist eine Methode, um den euklidischen Abstand jedes Punktes in eine bedingte Wahrscheinlichkeit anstelle der Ähnlichkeit umzuwandeln und auf eine niedrigere Dimension abzubilden.

Es gibt auch eine Methode namens Barnes-Hut t-SNE, die die Berechnungskosten auf Kosten der Genauigkeit verbessert. In Sklearn können Sie zwei Methoden auswählen: Exakt (Fokus auf Genauigkeit) und Barnes-Hut. Standardmäßig ist Barnes-Hut ausgewählt, und die Abstimmung ist auch durch Einstellen des optionalen Winkels möglich. Es wird auch häufig in Kaggle vorgestellt.

print("Computing t-SNE embedding")
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X)

plot_embedding(X_tsne,
               "t-SNE embedding of the digits (time %.2fs)" %
               (time() - t0))

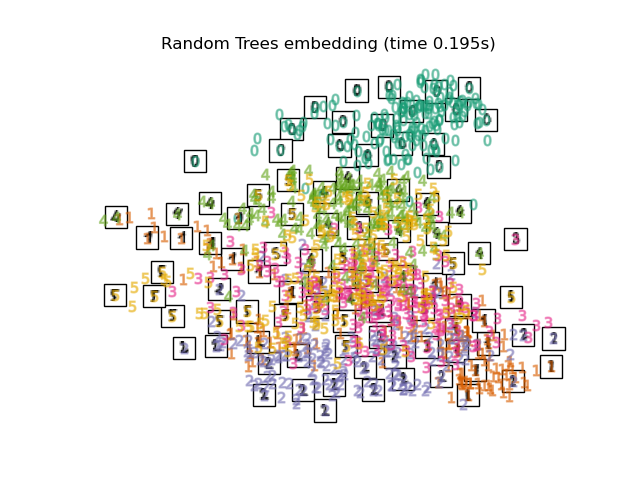
3.9. Random Forest Embedding

print("Computing Totally Random Trees embedding")
hasher = ensemble.RandomTreesEmbedding(n_estimators=200, random_state=0,
                                       max_depth=5)
t0 = time()
X_transformed = hasher.fit_transform(X)
pca = decomposition.TruncatedSVD(n_components=2)
X_reduced = pca.fit_transform(X_transformed)

plot_embedding(X_reduced,
               "Random forest embedding of the digits (time %.2fs)" %
               (time() - t0))

[PYTHON] Dimensionsreduktion hochdimensionaler Daten und zweidimensionales Plotverfahren