[PYTHON] (komplex) Es hängt davon ab, wie der Koeffizient des Morlet-Wavelets, der entsprechende Einstellwert und das Material benannt werden. Deshalb habe ich versucht, ihn so gut wie möglich zu organisieren.

Ich kann es nicht sehr gut organisieren, aber ...

1. Ich bin mir nicht sicher, ob die Variablen und Ausdrücke im Wavelet-Ausdruck geringfügig voneinander abweichen und auf genau dasselbe verweisen.

Ref. Aus dem Material von Matlab (wahrscheinlich) Teolis (1998) Computational Signal Proceesing with Wavelets. P66

Formel

Variablennamen

γb: benannte Varianz (Bandbreite). Wie fb in Matlab-Material. Es scheint eine zeitliche Streuung zu sein. Aber was ist hier zeitliche Streuung? Es heißt γc: Mittenfrequenz. Dies ist fast das gleiche. Ich verstehe, dass es der Wert ist, der durch Faktoren = np.arange (8,30) wie mne festgelegt wird. j: imaginäre Einheit

ref. stack overflow

Formel

w (t, f 0) = A ・ exp (–t 2 2/2 * σ 2 2) exp (2 * i * π * f 0 </ sub> * t) = A ・ exp (2 i & pgr; f 0 </ sub> t- (t 2 </ sup> / 2 & sgr; 2 </ sup>) >))

Variable

f _{0 </ sub>: Mittenfrequenz (γc oben, fc in der Matlab-Wavelet-Toolbox) Es wird beschrieben als & sgr;: & sgr; = m / 2 & pgr; f 0 & sub0; Im Vergleich zur obigen Teolis (1998) -Gleichung Es stimmt mit der Annahme überein, dass γb = 2σ2 </ sup> ist. m: konstant. Kompromiss zwischen Zeit- und Frequenzauflösung. Ich habe ihn auf 7 gesetzt. A = 1 / (σ (2π) ^{0,5 </ sup>) = 1 / (σ√2π): Der Teil vor e (exp) wird durch eine Variable ersetzt. Eingeführt unter dem Namen Normalisierungsfaktor Ja.}}

Ref. [Tallon-Baudry (1999)] 3, S. 154, Kasten 2 Beschreibung

Formel

w (t, f) = A. exp (- t 2 </ sup> / 2 & sgr; t </ sub> 2 </ sup>). exp (2i & pgr; ft): Dies ist Gleich wie Stapelüberlauf.

Variable

f: Wie f _{0 </ sub> oben. Mittenfrequenz σ t </ sub>: Wie oben σ. Beschrieben als Standardabweichung des Zeitbereichs.}

** A = 1 / (σt √π) 1/2 **: Es wird als Normalisierungsfaktor wie [Stapelüberlauf] 2 geschrieben. Die Formel ist etwas anders. [Tallon-Baudry (1997)] 11 Es hat die gleiche Beschreibung. Es ist nicht bekannt, ob es beabsichtigt oder falsch ist + Kopie.

ref. matlab wavelet toolbox

Formel

ψ (x) = 1 / √πfb * ** exp (x 2 </ sup> / fb) ** * exp (2iπfcx): Kopieren und Einfügen hat nicht funktioniert, also kopieren Sie es. Im Vergleich zu den beiden oben genannten hat ** exp (x ^{2 </ sup> / fb) ** kein ** Minus **. Diese Seite ist die einzige, daher habe ich das Gefühl, einen Fehler gemacht zu haben. .. Andere entsprechen Teolis (1998), Stapelüberlauf}

Variable

x: Wie t oben fc: Wie oben f0, f, γc. Mittenfrequenz fb: benannter Bandbreitenparameter. Wie γb in Teolis (1998).

ref. matlab help

Formel

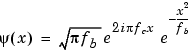Es ist auch ein bisschen anders. Der Nenner und das Molekül sind in dem Teil vor e umgekehrt (A: Normalisierungsfaktor, der oben erscheint). Der Unterschied zwischen dem Nenner und dem Molekül ist nur diese Seite, also ist es wahrscheinlich falsch. Andere entsprechen Teolis (1998), Stapelüberlauf

Variable

Die Benennung von fc und fb entspricht der von [matlab Wavelet Toolbox] 4.

Ref. [Stapelaustausch] 7 Wavelet cmor fb fc oder ähnliches wird die Spitze treffen.

Formel

Das Minus von e ^{-j2pifct </ sup> scheint unnötig.}

Zusammenfassung von 1

Umfassendes Urteil (komplex) Die Formel von Morlet Wavelt lautet Teolis (1998) Computational Signal Proceesing with Wavelets. P66, Stapelüberlauf scheint korrekt zu sein. Teolis (1998) ist ein Text. Die Formel unterscheidet sich je nach Material geringfügig, und ich habe das Gefühl, dass sie tatsächlich voller Fehler ist.

2. Was ist eine gute Einstellung für Wavelet? (Hauptsächlich mit Blick auf eine Python)

[Exkursion] 9(Zeit-Frequenz-Analyse, Wavelet-Abschnitt)

cfg.width. Bestimmt die ** Breite ** der Wavelets in Anzahl der Zyklen. In der Stichprobe

cfg.width      = 7; 

Es war. Ebenfalls, The spectral bandwidth at a given frequency F is equal to F/width*2 the wavelet duration is equal to width/F/pi F ist die Frequenz, die mit der obigen Mittenfrequenz (f, f 0, γc, fc) identisch zu sein scheint.

• Ich weiß nur nicht, was spektrale Bandbreite und Wavelet-Dauer bedeuten.
• Es scheint keine so einfache Beziehung zu sein, dass die spektrale Bandbreite mit σf </ sub> und die Wellenformdauer mit σt </ sub> übereinstimmt. Es gibt viele Begriffe und es ist verwirrend.

Tallon-Baudry(1999) ** σ f </ sub> = 1 / (2πσ t </ sub>) ** (Gleichung 2.1) Die Beziehung wird angezeigt.

--σt </ sub> wird als Standardabweichung (Zeitbereich) beschrieben. Es scheint dasselbe zu sein wie σt </ sub> und σ, die mehrmals aufgetreten sind. --σf </ sub> wird auch als Standardabweichung (Frequenzbereich) beschrieben.

** f / σ f </ sub> (konstantes Verhältnis: in der Praxis größer als fünf) ** (Gleichung 2.2).

• f scheint die gleiche zu sein wie die Mittenfrequenz (F in der Exkursion, f 0, γc, fc, die oben erscheint).

Roach & Mathalon (2008) ** σ t </ sub> = 1 / (2πσ f </ sub>) ** (Gleichung 2.3) Es ist dasselbe, wenn die Gleichung (2.1) von [Tallon-Baudry (1999)] 3 modifiziert wird.

Beschreibung der Variablen

σ t </ sub>: Beschrieben als zeitliche SD. σf </ sub>: spektrale Bandbreite um seine Mittenfrequenz f0, die eine SD von σf </ sub> hat, so dass gesagt werden kann, dass es sich um eine SD der Frequenz handelt. Morlet-Wavelet ist eine Gaußsche Hüllkurve ( Da das Wort "normalverteilte Hüllkurve" häufig vorkommt, kann SD leicht als Index in Form eines Wavelets verwendet werden. Nur am Ende der gleichen Seite spectral bandwidth around any given center frequency is mσ_f. Da ist auch ein. m wird multipliziert. Daraus schließen spectral bandwith = mσ_f , and has σ_f in it. Ich stelle mir vor, dass es bedeutet. Ich bin beunruhigt über die Beschreibung, die den Text verwirrt.

** c = f 0 </ sub> / & sgr; f </ sub> ** (Gleichung 2.4) Und ** c (konstantes Verhältnis) ** sind definiert ** (wahrscheinlich dasselbe wie cfg.width) **. Dies weist auch auf dasselbe hin, nur die Variable c wird Gleichung 2.2 zugewiesen. Es wird angenommen, dass es gibt.

• Im Text wird empfohlen, dass c eine Zahl von ungefähr 5,6,7 sein sollte, damit σ t </ sub> Wellen mit einem oder mehreren Zyklen enthält ("constan"). , c, wird typischerweise empfohlen, größer als 5 zu sein, und wird häufig auf Werte von 6 oder 7 eingestellt, was einem σt </ sub> entspricht, der dadurch mindestens einen vollständigen Sinuszyklus für eine bestimmte Frequenz ergibt ") .- -In [Stapelüberlauf] 2 erscheint die Formel ** σ = m / (2 π f <0> </ sub>) ** und (σ = σ t </ sub> (Vielleicht), was mit der folgenden Gleichung (2.5) übereinstimmt, so dass es scheint, dass m und das konstante Verhältnis c in dieser Gleichung auf dasselbe hinweisen.

Ein wenig beiseite: Erklärung, dass σ t </ sub> Wellen mit einem oder mehreren Zyklen enthält, wenn c ungefähr 7 ist (kann falsch sein)

Bei Transformation in die Form von σ t </ sub> = unter Verwendung der Gleichungen (2.3) und (2.4)

** σ t </ sub> = c / (2πf) = c / (2π) * 1 / f ** (Gleichung 2.5) wird erhalten.

• Da f die Frequenz ist, ist 1 / f die Zeit für einen Zyklus.
• Wenn also c / (2π) vor 1 / f 1 überschreitet, sollte σ t </ sub> Wellen mit einem oder mehreren Zyklen enthalten (warum eine solche Länge). Ich weiß nicht, warum Sie es brauchen), aber Sie können die Empfehlungen erfüllen. ―― 2π = 6,28 Da es ein wenig ist, wird angenommen, dass c / (2π)> 1 bei c = 7 und σt </ sub> Wellen mit mehr als einer Periode enthält.

** Unbekannte Variable m **

[Roach & Mathalon (2008)] 10 erklärt es als Faktor m. ** Das temporäre Fenster für eine gegebene Frequenz (f 0 </ sub>) ist m & sgr; t </ sub> ** (Gleichung 2.6). Ich bin mir nicht sicher, worauf sich das Zeitfenster bezieht. Ich habe jedoch das Gefühl, dass das zeitliche Fenster der Wavelet-Dauer entspricht, die in [Exkursion] 9 angezeigt wird. Lassen Sie uns den Ausdruck transformieren.

Aus den Gleichungen (2.6) und (2.5) zeitliches Fenster = mc / (2π) * 1 / f = mc / (2π) / f. Ich wiederhole die Beschreibung im obigen Abschnitt über Exkursionen.

** Wavelet-Dauer ** ist gleich ** Breite / F / pi ** (Gleichung 2.7) Da F = f unter der Annahme von c = Breite und m = 2, ist das zeitliche Fenster = Wavelet-Dauer Hält. ** temporäres Fenster ** (von Roach & Mathalon (2008)) ** = Wavelet-Dauer ** (nach Exkursion) sieht gut aus.

[Roach & Mathalon (2008)] 10 spectral bandwidth around any given center frequency is mσ_f Entspricht dies der spektralen Bandbreite in [Exkursion] 9? Ab Feldreise: spektrale Bandbreite = F / Breite * 2

Wenn die vorherige Breite = c korrekt ist, dann ist c = f 0 </ sub> / σ f </ sub> (Gleichung 2.4) Weil es gibt.

Roach & Mathalon (2008) spektrale Bandbreite = m & sgr; f </ sub> = mf 0 </ sub> / c = F / width * m (Feldauslösegleichung) Man kann also sagen, dass m = 2 auf dasselbe zeigt.

Sie können auch sagen, dass Fieldtrip cfg.width = c (konstantes Verhältnis).

Es gibt zu viele Begriffe. Es ist verwirrend. Übrigens gibt es in der Exkursion keine explizite Beschreibung, die diesem "m" entspricht. Wird es intern angemessen verarbeitet?

• [Roach & Mathalon (2008)] 10 Referenz, aber für [Tallon-Baudry (1997)] 11 "Wavelet-Dauer 2σ t </ sub> von etwa zwei Schwingungsperioden Die Beschreibung "Aktivität bei f 0 </ sub>" erscheint. Es scheint, dass sie auch hier als m = 2 behandelt wird.
• [Ford et al. (2008)] 14 geben an, dass "konstantes Verhältnis (σf = f / 7) und Wavelet-Dauer (4σt </ sub>)" "Spektralband mit 4σf </ sub> Es scheint, dass cfg.width = 7 (konstantes Verhältnis in anderen Dokumenten) in der Exkursion und m = 4 in [Roach & Mathalon (2008)] 10.
• "m wird für 6 empfohlen, es gibt jedoch auch Analysebeispiele für 4 und 2" ([Roach & Mathalon (2008)] 10).

MNE python

• Sie können die Häufigkeit mit tfr_morlet analysieren, aber es gibt ein solches Einstellungselement namens n_cycles. ――Ich weiß überhaupt nicht, ob n_cycles in der Beschreibung "Die Anzahl der Zyklen global oder für jede Frequenz" auf c, temporäre Dauer oder m zeigt.
• Wenn Sie sich die Analysebeispiele ansehen, sehen Sie 7 oder 2 oder freq / 2 oder freq / 3. ――So bin ich mir doch nicht sicher. Da das Einstellungsbeispiel 7 enthält, entspricht es möglicherweise der cfg.width of fieldtrip oder so.

Referenz: Wenn Sie sich das Morlet-Skript ansehen, das tfr_morlet intern verwendet

Das Skript enthält ein Def-Morlet in mne / time_frequency / tfr.py.

tfr.py

sigma_t = this_n_cycles / (2.0 * np.pi * f)

Daher denke ich aus Gleichung (2.5), dass this_n_cycles (= n_cycles) = c (konstantes Verhältnis) ist.

Zusammenfassung von 2

--cfg.width of fieldtrip und n_cycles of mne python, c (konstantes Verhältnis. Gleichung 2.4) im Dokument, m in [Stapelüberlauf] 2 scheint auf dasselbe zu verweisen. Ich kann nicht, aber ich möchte das konstante Verhältnis lesen und versuchen, es so gut wie möglich zu verstehen. Beachten Sie, dass m in [Roach & Mathalon (2008)] 10 anders ist.

• & sgr; t </ sub> ist eine temporäre SD, die sich von der Wavelet-Dauer unterscheidet (wahrscheinlich = temporäres Fenster). Wavelet-Dauer = m & sgr; t </ sub> ([Roach & Mathalon (2008)] [ Ab 10]
• In ähnlicher Weise ist & sgr; f </ sub> die Frequenz SD, die sich von der spektralen Bandbreite unterscheidet. Spektrale Bandbreite = m & sgr; f </ sub> (von [Roach & Mathalon (2008)] 10)
• Da ich oft die Einstellung 7 einschließlich der Erklärung des konstanten Verhältnisses sehe, ist es besser, zuerst die Einstellung cfg.width und n_cycles zu sehen.
• [Roach & Mathalon (2008)] m in 10 ist nicht explizit in mne python, fieldtrip (glaube ich) festgelegt. Fieldtrip ist m = 2. Ist mne nicht äquivalent?
• Es gibt ein Analysebeispiel wie n_cycles = 2 in mne python (es kann sich von Wavelet unterscheiden, da es ein Beispiel für [source_band_induced_power] ist 12). Es ist immer noch unbekannt, ob es die richtige Einstellung ist. [Roach & Mathalon (2008)] [ In 10] wird c als 5 oder mehr geschrieben, daher ist es möglich, dass n_cycles = c nicht auf dieser Abweichung basiert ... ――Ich verstehe den Unterschied zwischen Morlet und komplexem Morlet überhaupt nicht. Verlassen Sie sich also nicht darauf, sondern lassen Sie uns die Materialien einzeln treffen.