[PYTHON] Ford-Falkerson-Methode und ihre Anwendungen-Ergänzung zu Kapitel 8 der Algorithmus-Kurzreferenz-

Überblick

Dies ist eine Reihe von Büchern zu lesen, verschiedene Dinge neu zu studieren und zu schreiben, woran Sie interessiert sind. Diesmal [Algorithmus-Kurzreferenz](http://www.amazon.co.jp/%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82% BA% E3% 83% A0% E3% 82% AF% E3% 82% A4% E3% 83% 83% E3% 82% AF% E3% 83% AA% E3% 83% 95% E3% 82% A1% E3% 83% AC% E3% 83% B3% E3% 82% B9-George-T-Heineman / dp / 4873114284) Das Thema lautet "Netzwerkflussalgorithmus" in Kapitel 8. Insgesamt ist die Ford-Falkerson-Methode erstaunlich.

Hauptteil 1: Überblick über die Ford-Falkerson-Methode

Über verschiedene Größen in der Grafik

(Richtung) Wir gewichten häufig die Kanten in der Grafik. Die Menge dieses Gewichts beträgt

――Zeit und Entfernung --Es kostet,

• Einige Durchflussraten

Es entspricht verschiedenen Konzepten, aber alle sind als die gleiche "Seitengewichtung" formuliert.

Informationen zur Methode, diese Gewichtsmenge als Zeit und Entfernung zu verwenden und die Berechnung durchzuführen, die "wie lange es von einem bestimmten Startpunkt bis zum Zielpunkt dauern wird", finden Sie in der Dikstra in Kapitel 6. Ich denke nach dem Gesetz. In diesem Kapitel werden die im obigen Beispiel genannten Kosten und Durchflussraten betrachtet.

Ford Falkerson Methode und ihre Punkte

Betrachten Sie zunächst die Durchflussrate = Durchfluss. Es gibt eine Methode, die als Ford Falkerson-Methode bekannt ist. Ich denke, die Idee, die Anzahl der Möglichkeiten zur Erhöhung gierig zu erhöhen, ist relativ leicht zu verstehen, aber ich denke, der wichtige Punkt ist, "über den Fluss in die entgegengesetzte Richtung zur normalen Richtung nachzudenken". Hier werde ich versuchen, diese Idee mit einem Schwerpunkt zu erklären. Betrachten Sie der Übersichtlichkeit halber das folgende Diagramm, das auf jeder Seite ein Gewicht von 1 hat, und ermitteln Sie in diesem Diagramm den maximalen Durchfluss von S nach T. In dieser Grafik gibt es die folgenden drei Routen von S nach T, und alle Routen werden nur durch diese Route erschöpft. 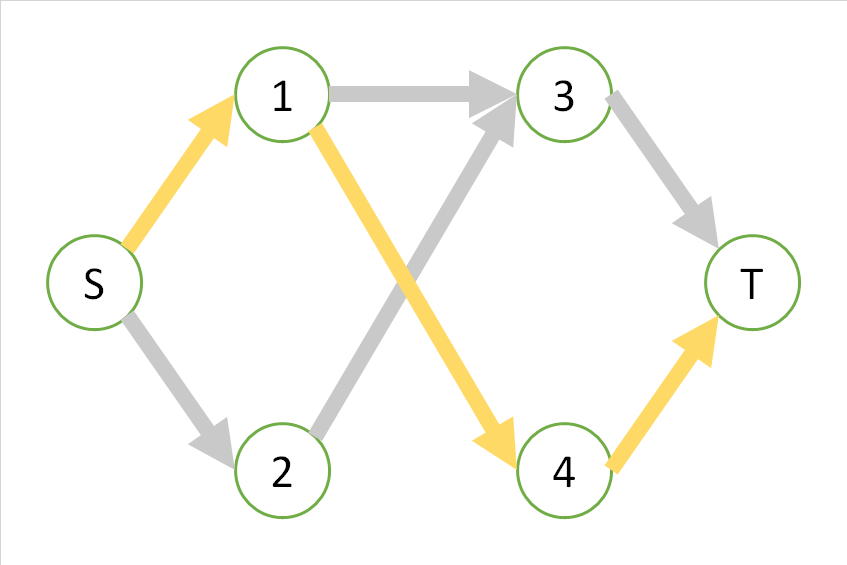Bei der ersten orangefarbenen Route kann diese Route derzeit nicht gleichzeitig mit der gelben und der blauen Route verwendet werden. In diesem Sinne können Sie, wenn Sie einen orangefarbenen Pfad nehmen, den Fluss nicht mehr erhöhen, "indem Sie dem orangefarbenen Pfad mehr parallele Pfade hinzufügen", und der Fluss scheint "maximal" zu sein. ..

Im Allgemeinen kann ein gieriger Algorithmus in einem geeigneten Maximalwert stecken bleiben, aber bei der Ford-Falkerson-Methode wird dies durch Berücksichtigung eines "Flusses einschließlich der umgekehrten Richtung" gelöst. Mit anderen Worten, wir glauben, dass die folgenden Routen existieren. Die Seiten 3 bis 1 sind im Originaldiagramm nicht vorhanden, nur die Seiten 1 bis 3 sind vorhanden, sodass die Farben geändert werden. Wenn Sie die Seite von 3 zu 1 als $ e_ {31} $ schreiben, ist dies $ e_ {31} = -e_ {13} $. Auch unter Berücksichtigung dieser Route ist die orangefarbene Route nicht mehr das Maximum, und der folgende Fluss kann berücksichtigt werden. Die Kanten zwischen 1 und 3 in dieser Abbildung heben sich schließlich gegenseitig auf und entsprechen denen, die nicht verwendet werden. Wenn Sie an etwas wie "imaginäre Straße" wie die 3: 1-Seite des aktuellen Beispiels denken, müssen Sie nicht in einen seltsamen Maximalwert fallen. Das heißt, es ist nicht offensichtlich, dass es nicht passt, also denke ich, dass es eine überraschende Behauptung ist. Obwohl der Beweis relativ einfach ist.

Was ich bisher gesagt habe Es ist auch so etwas. Und nach der Ford-Falkerson-Methode bedeutet dies, dass unabhängig davon, welche der drei "vorhandenen" Routen als Ausgangspunkt genommen wird, der zunehmende Pfad immer die linke oder rechte Seite dieser Gleichung erreicht. ich sage (Natürlich wird gesagt, dass die gleiche Bedeutung nicht nur in diesem Diagramm gilt, sondern auch in allgemeinen Diagrammen.) Dies ist eine ziemlich starke mathematische Eigenschaft und ich finde sie sehr interessant. In der Tat, wie man diese Routen nimmt

• Wenn Sie der Tiefe Vorrang einräumen möchten, verwenden Sie die ursprüngliche Ford Falkerson-Methode
• Wenn Sie der Breite Vorrang einräumen möchten, verwenden Sie die Edmonds Carp-Methode
• Wenn Sie sich entscheiden, die Kosten zu priorisieren, die primäre duale Methode, die die Lösung für das Problem des minimalen Kostenflusses darstellt

Sie können einen ähnlichen Algorithmus erhalten. Dahinter verbirgt sich, wie wir hier gesehen haben, die Tatsache, dass ** der maximale Durchfluss eine lineare Verbindung (Addition) der obigen Pfade ** zu sein scheint.

Um die Ford-Falkerson-Methode (Verallgemeinerung) grob in mathematischen Begriffen zu erklären,

――Klarieren Sie alle Routen von S nach T, einschließlich Routen mit umgekehrter Pfeilrichtung. In diesem Beispiel ist $ e_ {s1} + e_ {13} + e_ {3t}, e_ {s2} + e_ {23} -e_ {13} + e_ {14} + e_ {4t}, e_ {s1} + e_ {14} + e_ {4t}, e_ {s2} + e_ {23} + e_ {3t} $

• Setzen Sie für jede dieser Routen die Durchflussrate auf 1 und erstellen Sie die folgende Gleichung. Im Fall dieses Beispiels $\\begin{align}+e_{s1}&&+e_{13}&&+e_{3t}&= 1 \\\\ &+e_{s2}+e_{23}&-e_{13}&+e_{14}+e_{4t}&&= 1 \\\\ +e_{s1}&&&+e_{14}+e_{4t}&&= 1 \\\\ &+e_{s2}+e_{23}&&&+e_{3t}&= 1 \\end{align}$
• Unter dieser Bedingung möchte ich den Maximalwert der Summe dieser linearen Verbindungen ermitteln. Die Einschränkung ist $ 0 \ leq a_ {xy} \ leq $ (maximaler Durchfluss auf jeder Seite), wobei der Koeffizient von $ e_ {xy} $ $ a_ {xy} $ ist.
• Um $ a_ {xy} $ tatsächlich zu finden, fügen Sie Gleichungen hinzu, die die Randbedingungen von einem Ende aus erfüllen. ――Der Maximalwert wird unabhängig von der Art des Hinzufügens erreicht. Die Art des Hinzufügens wird jedoch entsprechend den Bedingungen wie Berechnungsgeschwindigkeit und Kosten geändert.

Es bedeutet das.

Hauptteil 2: Implementierung der Berechnung des minimalen Kostenflusses durch Python

Problemstellung

Zusätzlich zu der oben genannten Durchflussrate können nun für jede Seite Kosten definiert werden. Zu diesem Zeitpunkt möchten Sie möglicherweise die Kosten so niedrig wie möglich halten und gleichzeitig die Flussrate von $ x $ von S nach T sicherstellen. Betrachten Sie beispielsweise die Verarbeitung eines Artikels, der in der Primärfabrik $ A $ in der Sekundärfabrik $ B_1, B_2, B_3 $ hergestellt wurde, und dessen Speicherung im Geschäft $ C_1, C_2, C_3 $.

Angenommen, Sie haben die folgenden Durchflussraten und Kosten:

• (Vom Scheitelpunkt zum Scheitelpunkt (Durchflussrate, Kosten)) Format

Daten

edges = {('A', 'B1', (100, 10)),
 ('A', 'B2', (100, 5)),
 ('A', 'B3', (100, 6)),
 ('B1', 'C1', (11, 5)),
 ('B1', 'C2', (10, 9)),
 ('B1', 'C3', (14, 5)),
 ('B2', 'C1', (17, 9)),
 ('B2', 'C2', (12, 6)),
 ('B2', 'C3', (20, 7)),
 ('B3', 'C1', (13, 7)),
 ('B3', 'C2', (11, 6)),
 ('B3', 'C3', (13, 10))}

Stellen Sie unter diesen Bedingungen sicher, dass der Gesamtfluss von ** $ A $ 100 $ beträgt, um die Kosten so niedrig wie möglich zu halten **.

Das Problem der Synchronisierung aus einer Hand lösen und Einschränkungen hinzufügen

Zunächst werde ich das Format des Diagramms ein wenig ändern, um zu verdeutlichen, dass die Ford-Falkerson-Methode ein gültiges Problem ist.

Spüle hinzufügen

Dies ist wirklich ein formelles Problem, aber ich werde den Punkt $ D $ vor $ C_1, C_2, C_3 $ hinzufügen. Dies entspricht T in der bisherigen Erklärung. Die Kante von $ C_i $ zu $ D $ wird einheitlich auf $ (100,0) $ gesetzt. Dies hat offensichtlich keine wesentlichen Auswirkungen auf das Problem.

Quelle hinzufügen

Die sofortige Anwendung der Ford-Falkerson-Methode auf dieses Problem würde eine einfache maximale Durchflussrate ergeben, die mehr kosten würde als die Gesamtdurchflussrate von $ = 100 $. Fügen Sie also den Scheitelpunkt $ A '$ vor $ A $ hinzu. Die Seite von $ A '$ bis $ A $ ist $ (100,0) $. Unter diesen Bedingungen entspricht das Ermitteln der maximalen Durchflussrate eindeutig der Gesamtdurchflussrate von $ = 100 $ (vorausgesetzt, die maximale Durchflussrate in der ursprünglichen Grafik übersteigt 100 $). Tatsächlich beträgt der maximale Fluss im Originaldiagramm $ 121 $, daher ist diese Bedingung in Ordnung.

neu zeichnen

lösen

Ich werde etwas machen, das vorerst gelöst werden kann, ohne sich der Leistung bewusst zu sein.

Daten

edges = {("A'", 'A', (100, 0)),
 ('A', 'B1', (100, 10)),('A', 'B2', (100, 5)),('A', 'B3', (100, 6)),
 ('B1', 'C1', (11, 5)),('B1', 'C2', (10, 9)),('B1', 'C3', (14, 5)),
 ('B2', 'C1', (17, 9)),('B2', 'C2', (12, 6)),('B2', 'C3', (20, 7)),
 ('B3', 'C1', (13, 7)),('B3', 'C2', (11, 6)),('B3', 'C3', (13, 10)),
 ('C1', 'D', (100, 0)),('C2', 'D', (100, 0)),('C3', 'D', (100, 0))}

definition.py

#Holen Sie sich eine Liste der Pfade ... Das Ergebnis ist eine Liste der Kosten, eine Liste der Kanten, eine Liste der Koeffizienten
def getAllPath(edges, visited, f, t, r, c, e, a):
    if f == t:
        r.append((c,e,a))
    for k in neighbor[f].keys():
        if k not in visited:
            getAllPath(edges, visited + [f], k, t, r, c + neighbor[f][k][2], e + [neighbor[f][k][1]], a + [neighbor[f][k][0]])

#Gibt "den Maximalwert zurück, den der Pfad jetzt annehmen kann" für den Pfad
def getMaximalFlow(world, (c,e,a)):
    l = len(e)
    delta = float("inf")
    for i in range(0, l):
        if a[i] > 0:
            if delta > world[e[i]][0] - world[e[i]][1]:
                delta = world[e[i]][0] - world[e[i]][1]
        elif a[i] < 0:
            if delta > world[e[i]][1]:
                delta = world[e[i]][1]
        else:
            delta = 0
    return delta

#Aktualisieren Sie das Diagramm
def updateWorld(world, (c,e,a), delta):
    l = len(e)
    for i in range(0, l):
        world[e[i]] = (world[e[i]][0], world[e[i]][1] + a[i] * delta)

Die Namen der Variablen sind ziemlich gut. Übrigens, obwohl die Dateien getrennt sind, werden sie tatsächlich in einem anderen Block im ipython-Notizbuch (jupyter) ausgeführt. (Das heißt, Variablen usw. werden vererbt)

solve.py

neighbor = {}
world = {}
for (f,t,(v,c)) in edges:
    #Kostenwörterbuch
    if not f in neighbor.keys():
        neighbor[f] = {}
    neighbor[f][t] = (1,(f,t),c) #Gewichtsfaktor, Basis, Kosten
    if not t in neighbor.keys():
        neighbor[t] = {}
    neighbor[t][f] = (-1,(f,t),-c) #Gewichtsfaktor, Basis, Kosten
    #Wörterbuch zum Speichern des aktuellen Wertes
    world[(f,t)] = (v,0) #Maximalwert, aktueller Wert

r = []
getAllPath(edges,[],"A'",'D',r,0,[],[])
r.sort()

l = len(r)
i = 0
while i < l:
    delta = getMaximalFlow(world, r[i])
    if delta > 0:
        updateWorld(world, r[i], delta)
        i = 0
    else:
        i = i + 1

world

Ergebnis

{('A', 'B1'): (100, 25), ('A', 'B2'): (100, 49), ('A', 'B3'): (100, 26),
 ("A'", 'A'): (100, 100),
 ('B1', 'C1'): (11, 11), ('B1', 'C2'): (10, 0), ('B1', 'C3'): (14, 14),
 ('B2', 'C1'): (17, 17), ('B2', 'C2'): (12, 12), ('B2', 'C3'): (20, 20),
 ('B3', 'C1'): (13, 13), ('B3', 'C2'): (11, 11), ('B3', 'C3'): (13, 2),
 ('C1', 'D'): (100, 41), ('C2', 'D'): (100, 23), ('C3', 'D'): (100, 36)}

Es kann ein wenig verwirrend sein. In der Visualisierung sieht es so aus. Obwohl es teilweise geschnitten ist.

Als einfache Prüfmethode ist $ B_3 \ bis C_3 $ $ 2/13 $ und $ B_1 \ bis C_2 $ ist $ 0/10 $, aber dies ist eine sehr teure Straße, daher ist die Berechnung selbst Es passt. Wenn Sie die Geschwindigkeit bewerten möchten, sollten Sie sie mit dem Solver von Python (Networkx) vergleichen. Da es sich jedoch hauptsächlich um das Lernen handelt, ist der Vergleich minderwertig.

Andere Ergänzungen

Punkte bezüglich der Rückgabe

"Hinzufügen von Punkten und Kanten, die nicht im aktuellen Diagramm enthalten sind" ist eine gängige Methode, um auf ein anderes Problem im Zusammenhang mit dem Diagramm zu reduzieren. Es ist leicht zu verstehen, z. B. das Konvertieren eines ungerichteten Diagramms in ein gerichtetes Diagramm, das Hinzufügen eines neuen Knotens und einer neuen Kante am Anfang, das Hinzufügen eines neuen Knotens und einer neuen Kante am Ende usw. Es gibt andere Methoden, z. B. das Teilen des Knotens in zwei. (In diesem Fall ist $ A` $ eher das Teilen von Knoten als das Hinzufügen neuer Punkte.)

Code zum Zeichnen

drawGraphy.py

#Visualisierung
import networkx as nx
import matplotlib.pyplot as plt
import math

G = nx.DiGraph()
srcs, dests = zip(* [(fr, to) for (fr, to) in world.keys()])
G.add_nodes_from(srcs + dests)

for (s,r,(d,c)) in edges:
    G.add_edge(s, r, weight=20/math.sqrt(d))

#Position, Feinabstimmung
pos = {"A'"  : ([-0.55,0]),
       'A'  : ([0.25,0]),
       'B1' : ([1,-1.2]),
       'B2' : ([1,0]),
       'B3' : ([1,1.2]),
       'C1' : ([2,-1.2]),
       'C2' : ([2,0]),
       'C3' : ([2,1.2]),
       'D' : ([2.8,0]),
      }

edge_labels=dict([((f,t,),str(world[(f,t)][1]) + '/' + str(world[(f,t)][0]) )
             for (f,t) in world.keys()]) #Ändern Sie die Seitenbeschriftung entsprechend

plt.figure(1)
nx.draw_networkx(G, pos, with_labels=True)
nx.draw_networkx_edge_labels(G,pos,edge_labels=edge_labels,label_pos=0.74) #Dies wird ebenfalls entsprechend angepasst

plt.axis('equal')
plt.show()

Das Ende

Als nächstes kommt A *. Kapitel 7 ist auch Python. Übrigens gibt es andere Artikel in dieser Reihe wie folgt. Bucket-Sortierung und n log n wall-Ergänzung zu Kapitel 4 der Algorithmus-Kurzreferenz- * Ruby Aufteilung von Suche und Berechnung - Ergänzung zu Kapitel 5 der Algorithmus-Kurzreferenz- * Python Lösen des Labyrinths mit Python-Supplement zu Kapitel 6 der Algorithmus-Kurzreferenz- * Python [Dieser Artikel →] Ford-Falkerson-Methode und ihre Anwendung - Ergänzung zu Kapitel 8 der Algorithmus-Kurzreferenz- * Python