Hat zum ersten Mal einen Artikel als Job-Jagd-Story veröffentlicht.

Ich habe das IIC-Papier (Invariant Information Clustering) gelesen und implementiert, das als sehr genau gilt. IIC ist eine Clustering-Methode, bei der die Menge der gegenseitigen Informationen maximiert wird. Klicken Sie hier für IIC-Artikel (https://arxiv.org/pdf/1807.06653.pdf#page9)

Invariant Information Clustering for Unsupervised Image Classification and Segmentation Xu Ji, João F. Henriques, Andrea Vedaldi

Das verwendete Framework ist TensorFlow 2.0. Die Zieldaten sind die bekannten MNIST.

Über gegenseitige Information

Es gibt mehrere Interpretationen der Menge an gegenseitigen Informationen, aber ich werde eine einfache Methode wählen, die dieses maschinelle Lernen leicht erklärt.

Die Informationsentropie H (X) für die Wahrscheinlichkeitsverteilung X ist nachstehend definiert.

H(X) = -\sum_{i}x_{i} \ln x_{i}

Der Wert dieses Betrags steigt an, wenn sich die Verteilung einer gleichmäßigen Verteilung nähert, und wird 0, wenn die Verteilung gegen einen Punkt konvergiert. Der gegenseitige Informationsbetrag $ I $ kann als der Betrag bezeichnet werden, in dem die Sätze von Informationsentropien der beiden ** nicht unabhängigen ** Wahrscheinlichkeitsverteilungen $ X $ und $ Y $ übereinstimmen.

I(X, Y) = H(X) + H(Y) - H(X,Y)

Wie Sie der Abbildung entnehmen können, bringt die Maximierung des gegenseitigen Informationsbetrags $ I $ die Informationsentropie von $ X $ und $ Y $ näher und erhöht die Informationsentropie von $ X $ und $ Y $. Indem die Informationsentropie näher gebracht wird, das Ausdruckslernen des Netzwerks fortschreitet, und indem die Informationsentropie erhöht wird, wird verhindert, dass sich die Clusterbildung auf einen Punkt konzentriert (Reduktion).

Beim tatsächlichen Lernen wird die gleichzeitige Wahrscheinlichkeit von $ Z $, $ Z '$ berechnet, wenn die vom Netzwerk für das Bildpaar ausgegebene Softmax ($ X $, $ X' ) ( Z $, $ Z '$) ist. Maximiert die Menge an gegenseitiger Information über die Grenzwahrscheinlichkeiten $ P_ {x}, P_ {y} $ der symmetrischen Matrix $ P $. Die spezifische Formel der Verlustfunktion lautet wie folgt.

\begin{align}
I(P_{x}, P_{y}) &= -\sum_{i}P_{x(i)} \ln P_{x(i)}-\sum_{j}P_{y(j)} \ln P_{y(j)}+\sum_{i}\sum_{j}P_{(i, j)} \ln P_{(i, j)}\\
&=\sum_{i}\sum_{j}\bigl(P_{(i, j)}(-\ln P_{x(i)}-\ln P_{y(j)}+\ln P_{(i, j)})\bigr)\\
&=\sum_{i}\sum_{j}P_{(i, j)}・\ln \frac{P_{(i, j)}}{P_{x(i)} P_{y(j)}}
\end{align}

Machen Sie ein Paar Bilder

Zum Lernen ist es notwendig, ein Paar $ X '$ für das Bild $ X $ zu erstellen. $ X $, $ X '$ sind Datenpaare, die dasselbe Objekt enthalten. Es ist jedoch wünschenswert, dass die instanzspezifischen Details unterschiedlich sind. Der Punkt ist, dass die Netzwerkausgaben $ Z und Z '$ stark abhängig und nicht unabhängig sind, da sie dasselbe Objektpaar sind.

Im Allgemeinen wird $ X $ durch Hinzufügen von Operationen wie Skalieren, Verzerren (Verzerren), Drehen, Inversion und Ändern von Kontrast und Sättigung zu $ X '$. Dieses Mal wurden die folgenden 4 Operationen durchgeführt.

Originalbild	Drehung	Verzerrung	Binarisierung	Rauschen

Diese Operation wirkt sich stark auf das Lernen aus.

Netzwerkstruktur

Natürlich ist es besser, Transferlernen zu machen, aber diesmal ist es eine einfache Aufgabe, also habe ich einfach eine vertraute Form von Conv und BN gemacht. Gibt einen Softmax-Vorhersagevektor für ein 28x28x1-Eingabebild aus. Die Ausgabe $ Z $ ist MNIST-Clustering, 10 Dimensionen entsprechen der Anzahl der Beschriftungen. Die andere ist die Ausgabe, die bei der Methode "Overclustering" im Papier verwendet wird. Diese besteht aus 50 Dimensionen, was dem 5-fachen des Etiketts entspricht. Overclustering ist ein Mechanismus, bei dem das Netzwerk mehr Funktionen erhält, indem gleichzeitig mehr Clustering als die erwartete Anzahl von Clustering durchgeführt wird. Die Faltungsschichtgewichte werden für diese beiden Lernerfahrungen geteilt, aber die vollständig verbundenen Schichten verwenden unterschiedliche Gewichte.

def create_model(self):
    inputs = layers.Input((28,28,1))

    x = layers.Conv2D(32, 3, padding="same")(inputs)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    x = layers.MaxPooling2D(2)(x)

    x = layers.Conv2D(64, 3, padding="same")(x)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    x = layers.MaxPooling2D(2)(x)

    x = layers.Conv2D(128, 3, padding="same")(x)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    x = layers.MaxPooling2D(2)(x)

    x = layers.Conv2D(256, 3, padding="same")(x)
    x = layers.BatchNormalization()(x)
    x = layers.Activation("relu")(x)
    conv_out = layers.GlobalAveragePooling2D()(x)

    x = layers.Dense(128, activation="relu")(conv_out)
    x = layers.Dense(64, activation="relu")(x)
    Z = layers.Dense(10, activation="softmax")(x)

    x = layers.Dense(128, activation="relu")(conv_out)
    x = layers.Dense(64, activation="relu")(x)
    overclustering = layers.Dense(50, activation="softmax")(x)

    return Model(inputs, [Z, overclustering])

Definition der Verlustfunktion

Geben Sie die Modellstapeldaten der Bildpaare $ X, X '$ an, erhalten Sie die Ausgabe von $ Z, Z' $ und Overclustering und berechnen Sie die gegenseitige Informationsmenge für jedes Bild mit der IIC-Methode. Das Dokument enthält ein Beispiel für die Implementierung in Pytrch. Wenn es in TenosrFlow 2.0 umgeschrieben wird, wird es zum folgenden Code. Wir wollen die Menge an gegenseitigen Informationen maximieren, aber maschinelles Lernen minimiert sie, sodass die gesamte Verlustfunktion negativ multipliziert wird. Der endgültige Verlust ist der Durchschnitt aus Clustering und Overclustering, und der Gradient wird mit diesem Wert berechnet.

def IIC(self, z, z_, c=10):
    z = tf.reshape(z, [-1, c, 1])
    z_ = tf.reshape(z_, [-1, 1, c])
    P = tf.math.reduce_sum(z * z_, axis=0)  #Gleichzeitige Wahrscheinlichkeit
    P = (P + tf.transpose(P)) / 2  #Symmetrie
    P = tf.clip_by_value(P, 1e-7, tf.float32.max)  #Vorspannung, um eine logarithmische Divergenz zu verhindern
    P = P / tf.math.reduce_sum(P)  #Standardisierung
    
    #Periphere Wahrscheinlichkeit
    Pi = tf.math.reduce_sum(P, axis=0)
    Pi = tf.reshape(Pi, [c, 1])
    Pi = tf.tile(Pi, [1,c])
    Pj = tf.math.reduce_sum(P, axis=1)
    Pj = tf.reshape(Pj, [1, c])
    Pj = tf.tile(Pj, [c,1])

    loss = tf.math.reduce_sum(P * (tf.math.log(Pi) + tf.math.log(Pj) - tf.math.log(P)))

    return loss

@tf.function
def train_on_batch(self, X, X_):
    with tf.GradientTape() as tape:
        z, overclustering = self.model(X, training=True)
        z_, overclustering_ = self.model(X_, training=True)
        loss_cluster = self.IIC(z, z_)
        loss_overclustering = self.IIC(overclustering, overclustering_, c=50)

        loss = (loss_cluster + loss_overclustering) / 2

    graidents = tape.gradient(loss, self.model.trainable_weights)
    self.optim.apply_gradients(zip(graidents, self.model.trainable_weights))
    return loss_cluster, loss_overclustering

Lernergebnis

Lernparameter Optimierer ist Adams Rate 0,0001 batch_size ist 1000 Die Ergebnisse des Lernens bis zur Epoche 100 unter Verwendung der Bildpaare in jeder Konvertierungsoperation sind wie folgt.

Wenn wir uns das Diagramm ansehen, sehen wir, dass es besser ist, mehrere Conversions zu kombinieren, als die Conversion allein durchzuführen. Das Folgende ist das Training mit einem Bildpaar, das alle vier Transformationen mit den besten Ergebnissen durchlaufen hat. Die gemischte Matrix aus der Trainingsmatrix $ P $ und der Testdatenvorhersage (vertikale Achse ist die wahre Bezeichnung, horizontale Achse ist der Ausgabeindex). ) Ist ein aufgezeichnetes GIF.

Eigentlich habe ich mehr als 500 Epochen gelernt, aber ich denke, dass das Lernen fast abgeschlossen war, weil sich in mehr als 100 Epochen nicht viel geändert hat. In der Matrix $ P $ sind die Werte im Verlauf des Lernens diagonal angeordnet, da $ Z und Z '$ dieselbe Verteilung ausgeben. Sie können auch sehen, dass der Wert in Spalte 1 höher ist als die anderen. Die Beschriftungen 2 und 3 können in der gemischten Matrix nicht unterschieden werden, und es gibt zwei Spalten, die die Beschriftung 8 ausgeben. Obwohl nicht perfekt, lag die korrekte Antwortrate ohne Lehrer bei 85%.

Verbesserung

Nun ist es eine gute Idee, eine Konvertierung zu finden, die $ X '$ besser macht, um die Genauigkeitsrate zu erhöhen, aber wir werden die Genauigkeit verbessern, indem wir die Verlustfunktion entwickeln. Wenn man den Lernprozess früher betrachtet, scheint die Ursache des Clusterfehlers darin zu liegen, dass die peripheren Wahrscheinlichkeiten der Matrix $ P $ nicht gerade sind. Wenn Sie die Formel auf die Menge der gegenseitigen Informationen überprüfen, können Sie sehen, dass die Begriffe $ H (X) und H (Y) $ die Grenzwahrscheinlichkeiten ausgleichen. Aus diesem Grund habe ich beschlossen, diesem Abschnitt ein Alpha-Gewicht hinzuzufügen und es als Parameter zu verwenden.

    #Verlust plus Alpha
    loss = tf.math.reduce_sum(P * (alpha * tf.math.log(Pi) + alpha * tf.math.log(Pj) - tf.math.log(P)))

Das Ergebnis des Lernens mit Alpha auf 10 ist wie folgt.

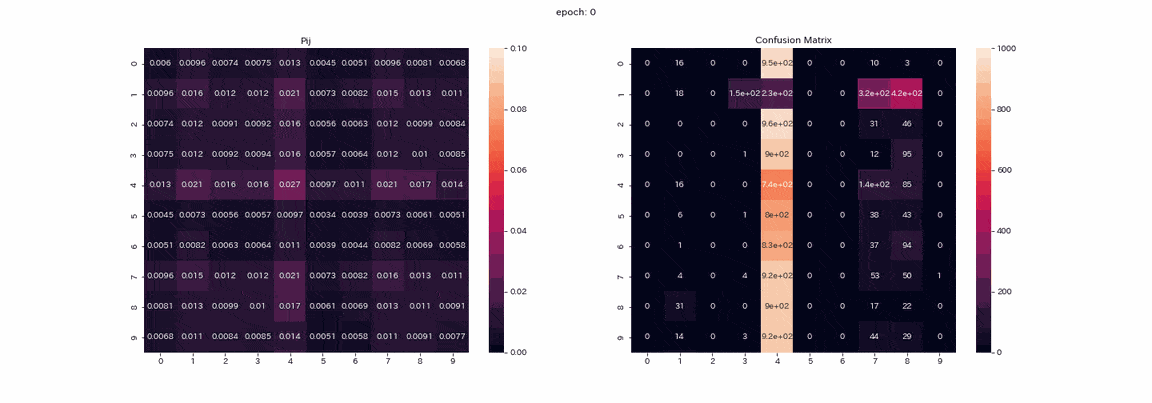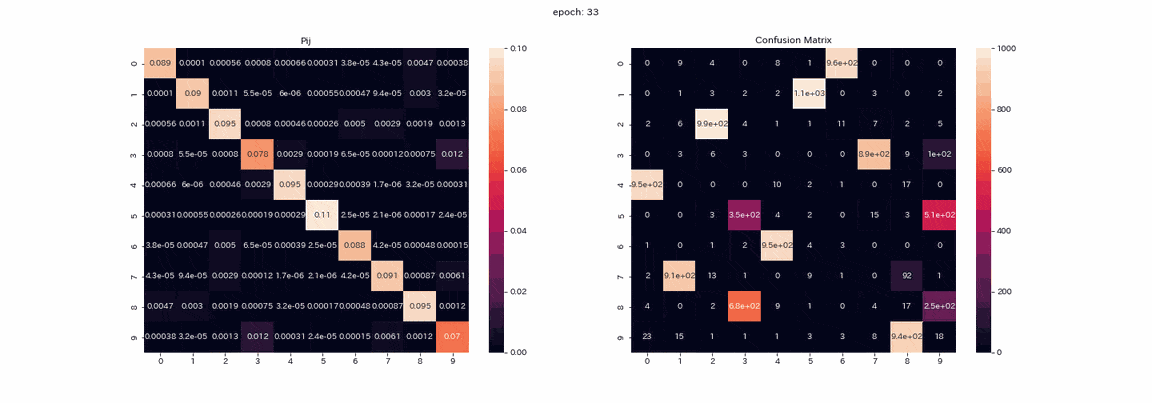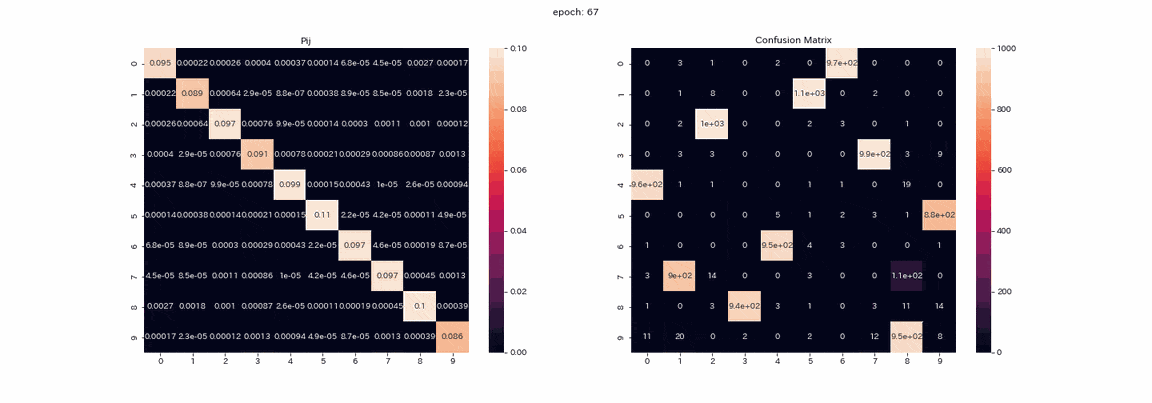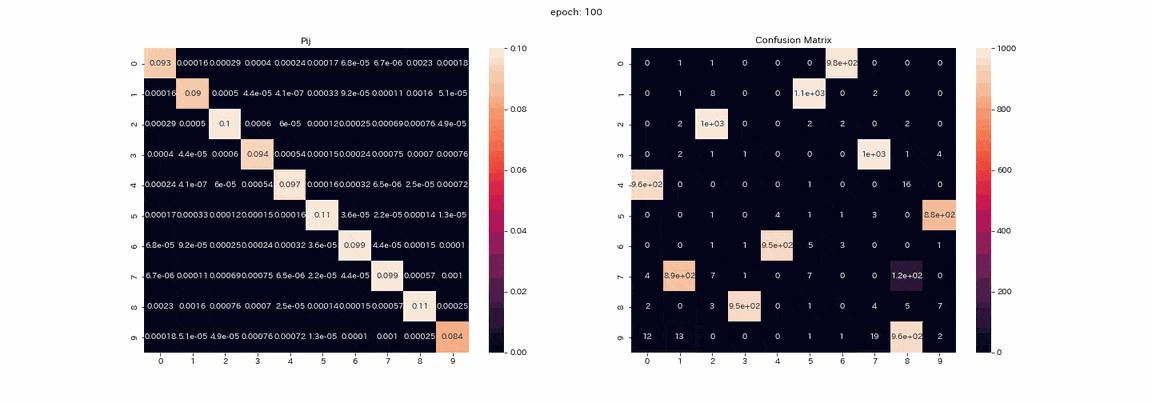
![rsbn_loss_matrix-compressor.gif](https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/340563/7c501a33-c153-b365-5d7e-7e8cea89fa58.gif)

Das Lernen ist stabil und fast alle Cluster sind erfolgreich. Die höchste Genauigkeitsrate lag bei 97,5%, was ziemlich genau war.

Bonus

Ich war neugierig, was für eine Klassifizierung Overclustering ist, also überprüfen Sie es. Unten finden Sie eine gemischte Matrix aus Overclustering (50 Dimensionen) im genauesten Modell. Es kann bestätigt werden, dass auch hier alle Etiketten klassifiziert werden können. Ein Teil der Spalten 9, 23, 40 von Etikett 7 wird angezeigt.

Spalte 9	Spalte 23	Spalte 40

Jedes erfasst die Eigenschaften des Schreibens von "7". Ist der Unterschied zwischen den Spalten 9 und 40 die Dicke der Linie? Wenn ich andere Zahlen nachschlug, wurden die Cluster oft durch den Unterschied in der Dicke getrennt, aber dies scheint auf die Art der Faltungsschicht zurückzuführen zu sein. Es ist Spalte 23, auf die ich achten möchte. Ich habe alles überprüft, aber fast alle "7", die in zwei Strichen geschrieben wurden und mit denen ich nicht vertraut bin, passen in Spalte 23. Ich hatte das Gefühl, dass die Möglichkeit, diese "7" zu klassifizieren und abzurufen, das Potenzial hat, neue Labels zu erstellen, die über die Lehrerdaten hinausgehen.

Das IIC-Papier zeigt, dass es sich um eine Methode handelt, die auch auf die Segmentierung angewendet werden kann, und es scheint, dass sie auf verschiedene Aufgaben angewendet werden kann, solange die Menge der gegenseitigen Informationen berechnet werden kann. Es war eine Methode voller romantischer Darbietungen, für die keine Lehrerdaten erforderlich waren.

[PYTHON] Eine einfache Methode, um eine korrekte MNIST-Antwortrate von 97% oder mehr zu erhalten, indem Sie ohne Lehrer lernen (ohne Transferlernen).