[PYTHON] Übersetzen Erste Schritte mit TensorFlow

Ich habe beschlossen, TensorFlow zu starten. Als Tutorial hat MNIST usw. bereits eine japanische Übersetzung des Vorgängers, daher habe ich beschlossen, Erste Schritte mit TensorFlow (https://www.tensorflow.org/get_started/get_started) (Stand: 11. März 2017) zu übersetzen, die ich nicht finden konnte tat.

Bitte weisen Sie auf Fehler hin.

Getting Started With TensorFlow

Mit dieser Anleitung können Sie in TensorFlow programmieren. Bitte TensorFlow installieren, bevor Sie dieses Handbuch verwenden. Um dieses Handbuch optimal nutzen zu können, müssen Sie Folgendes wissen:

• So programmieren Sie in Python
• Was Sie zumindest ein wenig über Arrays wissen ――Idealerweise etwas über maschinelles Lernen. Wenn Sie nicht wenig oder gar nichts wissen, ist dies Ihre erste Anleitung, die Sie lesen sollten.

TensorFlow bietet mehrere APIs. Die niedrigste API (TensorFlow Core) bietet Ihnen vollständige Programmiersteuerung. TensorFlow Core wird Forschern des maschinellen Lernens und anderen empfohlen, die eine genauere Kontrolle über ihre Modelle benötigen. Übergeordnete APIs sind normalerweise einfacher zu erlernen und zu verwenden als TensorFlow Core. Darüber hinaus machen diese übergeordneten APIs sich wiederholende Aufgaben für verschiedene Benutzer einfacher und konsistenter. Übergeordnete APIs wie tf.contrib.learn helfen bei der Verwaltung von Datensätzen, Schätzern sowie Schulungen und Inferenzen. Einige der High-Level-APIs von TensorFlow (ihre Methodennamen enthalten "Contrib") befinden sich in der Entwicklung. Einige Contrib-Methoden können sich in der nächsten TensorFlow-Version ändern oder veraltet sein.

Diese Anleitung beginnt mit TensorFlow Core. Danach werde ich erklären, wie dasselbe Modell mit tf.contrib.learn implementiert wird. Die Kenntnis der Prinzipien von TensorFlow Core bietet ein sehr gutes mentales Modell für die interne Funktionsweise bei Verwendung einer kompakteren API auf hoher Ebene.

Tensors Die zentrale Dateneinheit in TensorFlow ist ein Tensor. Ein Tensor besteht aus einer Reihe von Grundwerten in Form eines Arrays mit einer beliebigen Anzahl von Dimensionen.

3 # Rang 0 Tensor; Dies ist ein Skalar mit der Form []. [1., 2., 3.] # Rang 1 Tensor; Dies ist ein Vektor mit Form [3]. [[1., 2., 3.], [4., 5., 6.]] # Rang 2 Tensor; Form [2, 3] Matrix. [[[1., 2., 3.]], [[7., 8., 9.]] # Form [2, 1, 3], Rang 3 Tensor

TensorFlow Core tutorial TensorFlow importieren

Die Standardbeschreibung eines TensorFlow-Imports ist unten: import tensorflow as tf

Dadurch erhält Python Zugriff auf alle TensorFlow-Klassen, -Methoden und -Symbole. In den meisten Abschnitten dieses Dokuments wird davon ausgegangen, dass Sie dies bereits getan haben.

Berechnungsdiagramm

Sie könnten denken, dass das TensorFlow Core-Programm aus zwei separaten Abschnitten besteht.

1. Erstellen Sie ein Berechnungsdiagramm
2. Führen Sie das Berechnungsdiagramm aus

** Berechnungsdiagramm ** ist eine Reihe von TensorFlow-Operationen, die in einem Diagramm mit mehreren Knoten angeordnet sind. (Ein Berechnungsdiagramm ist eine Reihe von TensorFlow-Operationen, die in einem Diagramm von Knoten angeordnet sind.) Erstellen wir ein einfaches Berechnungsdiagramm. Jeder Knoten nimmt null oder mehr Tensoren als Eingabe und gibt einen Tensor aus. Ein Knotentyp ist eine Konstante. Alle TensorFlow-Konstanten nehmen keine Eingabe und geben die darin gespeicherten Werte aus. Sie können zwei Floating-Fraction-Tensoren "node1" und "node2" wie folgt erstellen:

node1 = tf.constant(3.0, tf.float32)

node2 = tf.constant (4.0) # Implizit tf.float32 print(node1, node2)

Das Ergebnis der endgültigen Druckanweisung sieht folgendermaßen aus Tensor("Const:0", shape=(), dtype=float32) Tensor("Const_1:0", shape=(), dtype=float32)

Beachten Sie, dass beim Drucken des Knotens nicht die erwarteten Werte für "3.0" oder "4.0" gedruckt werden. Stattdessen handelt es sich um Knoten, die bei der Auswertung 3.0 bzw. 4.0 ausgeben. Berechnungsgraphen müssen innerhalb von ** Sitzung ** berechnet werden, um den Knoten richtig bewerten zu können. Sitzungen enthalten die Kontrolle und den Status der TensorFlow-Laufzeit.

Der folgende Code erstellt ein "Session" -Objekt und ruft dann seine "run" -Methode auf, um den Berechnungsgraphen so weit auszuführen, dass "node1" und "node2" ausgewertet werden. Wenn Sie das Berechnungsdiagramm in einer Sitzung wie folgt ausführen:

sess = tf.Session()
print(sess.run([node1, node2]))

Sie können die erwarteten Werte für 3.0 und 4.0 sehen:

[3.0, 4.0]

Sie können komplexere Berechnungen erstellen, indem Sie den Tensor-Knoten mit Operationen kombinieren (Operationen sind auch Knoten). Sie können beispielsweise zwei konstante Knoten hinzufügen, um ein neues Diagramm zu erstellen, wie unten gezeigt:

node3 = tf.add(node1, node2)
print("node3: ", node3)
print("sess.run(node3): ",sess.run(node3))

Die letzten beiden Druckanweisungen werden gedruckt:

node3:  Tensor("Add_2:0", shape=(), dtype=float32)
sess.run(node3):  7.0

TensorFlow bietet ein Dienstprogramm namens TensorBoard, mit dem Bilder von Rechengraphen angezeigt werden können. Hier ist ein Screenshot, der zeigt, wie TensorBoard ein Diagramm visualisiert:

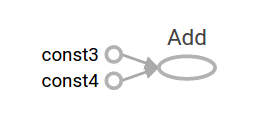
Bei dieser Rate ist dieses Diagramm nicht besonders interessant, da es immer das gleiche Ergebnis ausgibt. Diagramme können so parametriert werden, dass sie externe Eingaben akzeptieren, die als ** Platzhalter ** bezeichnet werden. ** Platzhalter ** sind Vorhersagen für die spätere Bereitstellung von Werten.

a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
adder_node = a + b  # + provides a shortcut for tf.add(a, b)

Die drei obigen Zeilen sind wie Funktionen oder Lambdas. Definieren Sie zwei Eingabeparameter (a und b) und dann deren Operationen. Dieses Diagramm kann mit mehreren Eingaben ausgewertet werden. Verwenden Sie den Parameter feed_dict, um den Tensor zu identifizieren, der bestimmte Werte für diese Platzhalter bereitstellt.

print(sess.run(adder_node, {a: 3, b:4.5}))
print(sess.run(adder_node, {a: [1,3], b: [2, 4]}))

Das Ausgabeergebnis ist

7.5
[ 3.  7.]

In TensorBoard sieht das Diagramm folgendermaßen aus:

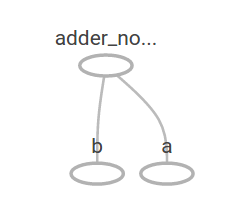
Sie können komplexere Berechnungsdiagramme erstellen, indem Sie andere Operationen hinzufügen. Zum Beispiel

add_and_triple = adder_node * 3.
print(sess.run(add_and_triple, {a: 3, b:4.5}))

Das Ausgabeergebnis ist

22.5

Das vorherige Berechnungsdiagramm sieht auf TensorBoard folgendermaßen aus:

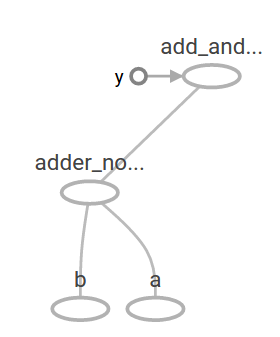
Beim maschinellen Lernen wollen wir normalerweise ein Modell, das mehrdeutige Eingaben wie eine der oben genannten annehmen kann. Um das Modell trainierbar zu machen, müssen wir in der Lage sein, das Diagramm so zu ändern, dass wir für dieselbe Eingabe eine neue Ausgabe erhalten. ** Variablen ** ermöglichen es Ihnen, Ihrem Diagramm lernbare Parameter hinzuzufügen. Sie bestehen aus Typ und Anfangswert:

W = tf.Variable([.3], tf.float32)
b = tf.Variable([-.3], tf.float32)
x = tf.placeholder(tf.float32)
linear_model = W * x + b

Die Konstante wird initialisiert, wenn Sie "tf.constant" aufrufen, und ihr Wert ändert sich nicht. Im Gegensatz dazu werden Variablen nicht initialisiert, wenn Sie "tf.Variable" aufrufen. Damit das TensorFlow-Programm alle Variablen initialisieren kann, müssen Sie die folgenden speziellen Operationen explizit ausführen:

init = tf.global_variables_initializer()
sess.run(init)

Es ist wichtig zu erkennen, dass "init" das Handle des TensorFlow-Subgraphen ist, der alle globalen Variablen initialisiert. Diese Variablen werden erst initialisiert, wenn Sie sess.run aufrufen.

Da "x" ein Platzhalter ist, können Sie "linear_model" für mehrere Werte "x" gleichzeitig auswerten:

print(sess.run(linear_model, {x:[1,2,3,4]}))

Die Ausgabe ist

[ 0. 0.30000001 0.60000002 0.90000004]

Wir haben ein Modell erstellt, wissen aber nicht, wie gut es ist. Um das Modell mit Trainingsdaten auszuwerten, benötigen wir einen Platzhalter "y", der den gewünschten Wert liefert, und wir müssen eine Fehlerfunktion schreiben.

Die Fehlerfunktion misst, wie weit das aktuelle Modell von den bereitgestellten Daten entfernt ist. Wir werden das Standardverlustmodell für die lineare Regression verwenden, bei dem es sich um die Summe der Quadrate der Deltas zwischen dem aktuellen Modell und den bereitgestellten Daten handelt. linear_model-y erzeugt einen Vektor, in dem jedes Element dem Fehlerdelta eines Beispiels entspricht. Rufen Sie "tf.square" auf, um diese Fehler zu quadrieren. Verwenden Sie dann tf.reduce_sum, um alle quadratischen Fehler zu summieren und einen Skalar zu erstellen, der die Fehler aller Stichproben extrahiert:

y = tf.placeholder(tf.float32)
squared_deltas = tf.square(linear_model - y)
loss = tf.reduce_sum(squared_deltas)
print(sess.run(loss, {x:[1,2,3,4], y:[0,-1,-2,-3]}))

Der Fehlerwert ist

23.66

Dies kann behoben werden, indem die perfekten Werte -1 und 1 für "W" und "b" manuell neu zugewiesen werden. Die Variable wird mit dem in "tf.Variable" angegebenen Wert initialisiert, kann jedoch durch eine Operation wie "tf.assign" geändert werden. Zum Beispiel sind "W = -1" und "b = 1" die besten Parameter für unser Modell. Sie können W und b wie folgt ändern:

fixW = tf.assign(W, [-1.])
fixb = tf.assign(b, [1.])
sess.run([fixW, fixb])
print(sess.run(loss, {x:[1,2,3,4], y:[0,-1,-2,-3]}))

Der endgültige Ausdruck zeigt an, dass der Fehler Null ist.

0.0

Ich habe die "perfekten" Werte für "W" und "b" erraten, aber der springende Punkt beim maschinellen Lernen ist, automatisch die richtigen Modellparameter zu finden. Wir werden im nächsten Abschnitt sehen, wie dies erreicht werden kann.

tf.train API Eine vollständige Erörterung des maschinellen Lernens würde den Rahmen dieses Lernprogramms sprengen. TensorFlow bietet jedoch ** Optimierer **, die jede Variable langsam ändern, um die Fehlerfunktion zu minimieren. Der einfachste Optimierer ist ** Gradientenabstieg **. Es ändert jede Variable um die Größe des Differentials für jede Variable in der Fehlerfunktion. Im Allgemeinen ist die manuelle Berechnung symbolischer Differenzen mühsam und fehleranfällig. Infolgedessen kann TensorFlow das Differential automatisch berechnen, indem einfach eine Beschreibung des Modells mit der Funktion tf.gradients angegeben wird. Einfach ausgedrückt, der Optimierer erledigt dies normalerweise für Sie. Zum Beispiel

optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)

sess.run(init) # reset values to incorrect defaults.
for i in range(1000):
  sess.run(train, {x:[1,2,3,4], y:[0,-1,-2,-3]})

print(sess.run([W, b]))

Der letzte Modellparameter ist: [array([-0.9999969], dtype=float32), array([ 0.99999082], dtype=float32)]

Ich konnte tatsächlich Maschinen lernen! Diese einfache lineare Regression erfordert nicht viel TensorFlow-Kerncode, aber es wird mehr Code benötigt, um ein Modell mit komplexeren Modellen und Methoden bereitzustellen. Daher bietet TensorFlow eine höhere Abstraktionsebene für allgemeine Muster, Strukturen und Merkmale. Im nächsten Abschnitt erfahren Sie, wie Sie diese Abstraktionen verwenden.

Komplettes Programm

Die Vollversion des trainierbaren linearen Regressionsmodells ist unten dargestellt:

import numpy as np
import tensorflow as tf

#Modellparameter W = tf.Variable([.3], tf.float32) b = tf.Variable([-.3], tf.float32) #Modelleingabe und -ausgabe x = tf.placeholder(tf.float32) linear_model = W * x + b y = tf.placeholder(tf.float32) #Error loss = tf.reduce_sum(tf.square(linear_model - y)) # sum of the squares #Optimierer optimizer = tf.train.GradientDescentOptimizer(0.01) train = optimizer.minimize(loss) #Trainingsdaten x_train = [1,2,3,4] y_train = [0,-1,-2,-3]

Trainingsschleife

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init) # reset values to wrong
for i in range(1000):
  sess.run(train, {x:x_train, y:y_train})

Bewerten Sie die Genauigkeit des Trainings

curr_W, curr_b, curr_loss  = sess.run([W, b, loss], {x:x_train, y:y_train})
print("W: %s b: %s loss: %s"%(curr_W, curr_b, curr_loss))

Beim Ausführen sieht es so aus:

W: [-0.9999969] b: [ 0.99999082] loss: 5.69997e-11

Dieses komplexere Programm kann mit TensorBoard visualisiert werden

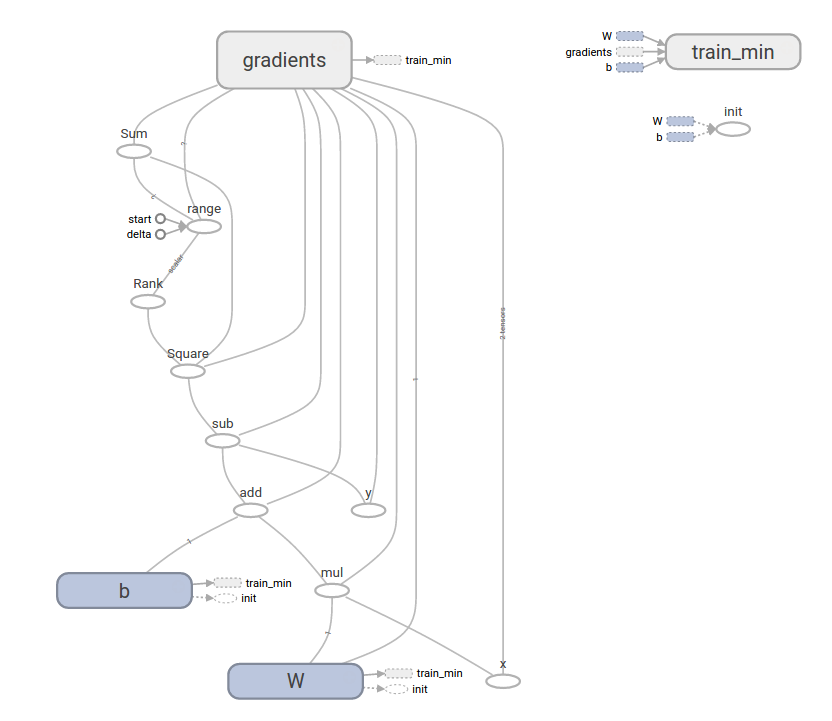
tf.contrib.learn

tf.contrib.learn ist eine TensorFlow-Bibliothek auf hoher Ebene, die das Verhalten beim maschinellen Lernen vereinfacht. Beinhaltet:

• Führen Sie eine Trainingsschleife aus
• Führen Sie die Auswertungsschleife aus
• Datensätze verwalten
• Fütterung verwalten

tf.contrib.learn definiert viele gängige Modelle.

Grundlegende Verwendung

Sehen Sie, wie einfach ein einfaches lineares Regressionsprogramm mit tf.contrib.learn sein kann:

import tensorflow as tf

#NumPy wird häufig zum Lesen, Bearbeiten und Vorverarbeiten von Daten verwendet. import numpy as np

Deklarieren Sie eine Liste der Funktionen. Im Moment benutze ich nur eine echte Funktion. Komplizierter und bequemer

Es gibt viele andere Arten von Spalten

features = [tf.contrib.layers.real_valued_column("x", dimension=1)]

#Estimator ist ein Frontend für Training (Anpassung) und Bewertung (Schätzung). #Lineare Regression, logistische Regression, lineare Klassifizierung, logistische Klassifizierung,

Und wie viele Klassifikatoren und Regressionen für neuronale Netze

Es gibt viele bereits definierte Typen.

Sie können einen linearen Klassifizierungsschätzer mit dem folgenden Code verwenden.

estimator = tf.contrib.learn.LinearRegressor(feature_columns=features)

#TensorFlow enthält viele Hilfsmethoden zum Laden und Einrichten von Datasets.

Hier verwenden wir numpy_input_fn.

Die Anzahl der Stapel (num_epochs) der erforderlichen Daten und

Geben Sie der Funktion an, wie groß jede Charge sein soll.

x = np.array([1., 2., 3., 4.])
y = np.array([0., -1., -2., -3.])
input_fn = tf.contrib.learn.io.numpy_input_fn({"x":x}, y, batch_size=4,
                                          num_epochs=1000)

Durch Aufrufen der # fit -Methode und Angabe des Trainingsdatensatzes

Sie können 1000 Trainingsschritte starten.

estimator.fit(input_fn=input_fn, steps=1000)

Hier werde ich bewerten, wie gut dieses Modell ist. In einem realen Beispiel

Ich möchte einen Datensatz mit einer separaten Validierung testen, um ein Übertraining zu verhindern.

estimator.evaluate(input_fn=input_fn)

Beim Ausführen sieht das Ergebnis so aus

{'global_step': 1000, 'loss': 1.9650059e-11}

Benutzerdefiniertes Modell

tf.contrib.learn hält Sie nicht in einem vordefinierten Modell. Angenommen, Sie möchten ein benutzerdefiniertes Modell erstellen, das nicht in TensorFlow integriert ist. Sie können den Datensatz "tf.contrib.learn" und allgemeine Abstraktionen wie Füttern, Training usw. beibehalten. Zur Veranschaulichung zeige ich Ihnen, wie Sie Ihr eigenes Modell erstellen, das "LinearRegressor" entspricht, indem Sie die TensorFlow-API auf niedrigerem Niveau kennen.

Verwenden Sie "tf.contrib.learn.Estimator", um ein benutzerdefiniertes Modell zu definieren, das mit "tf.contrib.learn" funktioniert. Tatsächlich ist "tf.contrib.learn.LinearRegressor" eine Unterklasse von "tf.contrib.learn.Estimator". Anstatt "Estimator" in eine Unterklasse zu unterteilen, stellen wir "Estimator" nur der Funktion "model_fn" zur Verfügung, die "tf.contrib.learn" mitteilt, wie Vorhersagen, Trainingszahlen und Fehler bewertet werden. .. Der Code sieht folgendermaßen aus:

import numpy as np
import tensorflow as tf

Deklarieren Sie eine Liste der Funktionen. Im Moment benutze ich nur eine echte Funktion

def model(features, labels, mode):

Erstellen Sie ein lineares Modell, um Werte vorherzusagen

  W = tf.get_variable("W", [1], dtype=tf.float64)
  b = tf.get_variable("b", [1], dtype=tf.float64)
  y = W*features['x'] + b

Fehler-Subgraph

  loss = tf.reduce_sum(tf.square(y - labels))

Trainingsuntergraph

  global_step = tf.train.get_global_step()
  optimizer = tf.train.GradientDescentOptimizer(0.01)
  train = tf.group(optimizer.minimize(loss),
               tf.assign_add(global_step, 1))

#ModelFnOps für die richtige Funktionalität (Funktionalität)

Kombinieren Sie die bisher erstellten Untergraphen

  return tf.contrib.learn.ModelFnOps(
  mode=mode, predictions=y,
  loss=loss,
  train_op=train)

estimator = tf.contrib.learn.Estimator(model_fn=model)

#Dataset Definition x = np.array([1., 2., 3., 4.]) y = np.array([0., -1., -2., -3.]) input_fn = tf.contrib.learn.io.numpy_input_fn({"x": x}, y, 4, num_epochs=1000)

Ausbildung

estimator.fit(input_fn=input_fn, steps=1000)

Bewerten Sie das Modell

print(estimator.evaluate(input_fn=input_fn, steps=10))

Das Ausführungsergebnis ist wie folgt

{'loss': 5.9819476e-11, 'global_step': 1000}

Beachten Sie, dass der Inhalt der benutzerdefinierten Funktion model () einer Schleife sehr ähnlich ist, die ein Modell manuell über eine API auf niedriger Ebene trainiert.

Nächster Schritt

Ich habe nützliche Grundkenntnisse in TensorFlow. Wir haben einige Tutorials vorbereitet, damit Sie mehr erfahren. Wenn Sie ein Anfänger im maschinellen Lernen sind, MNIST für Anfänger, andernfalls Deep MNIST für Experten Siehe (/ get_started / mnist / pros).

Sofern nicht anders angegeben, lautet der Inhalt dieser Seite Creative Commons Attribution 3.0 License und der Code lautet [Apache 2.0 License](http: // www). Es ist unter .apache.org / licenses / LICENSE-2.0 lizenziert. Weitere Informationen finden Sie unter Site-Richtlinien. Java ist eine eingetragene Marke von Oracle und seinen verbundenen Unternehmen.

Letzte Aktualisierung 8. März 2017